毫米波信道学习记录

毫米波信道学习记录

写在前

在初次接触毫米波信道的学习过程中，看到了知乎作者 “@张马也” 以及CSDN作者 “B417科研笔记” 的学习笔记，获益匪浅。为了便于个人学习，遂整理如下笔记，仅搬运和分享他们的学习成果，也会添加一些个人理解，仅做记录和分享，再次感谢你们作为科研工作者的分享与交流。
原链接：
https://www.cnblogs.com/MayeZhang/p/12374196.html
https://blog.csdn.net/weixin_39274659/article/details/104434934

MIMO信道回顾

MIMO无线信道的数学模型中，$h_{i,j}$ 是发射端第 $i$ 根天线和接收端第 $j$ 根天线的复信道增益，该增益来源于多条射线的叠加，每条射线是经过多条不同的路径到达接收机的 $$h_{i,j}=\sum _i{a}^i{e}^{j{\theta }_t}$$ 信道增益的模 $|h_{i,j}|$ 服从瑞利分布，如果除了大量的散射体还有一个很强的直射LoS路径，则信道增益的模 |hi,j| 服从莱斯分布。

• 注意：$h_{i,j}$ 是发射端第 $i$ 根天线和接收端第 $j$ 根天线之间的子信道，也是由一堆不同的路径叠加而成的，而不是仅指一条路径！
• 对于低频情况下，可以直接假设每一个子信道 $h_{i,j}$ 服从瑞利 或 莱斯分布。

毫米波信道

毫米波信道中一般有2-4个多径，时延扩展很小，k因子很大，从而可以简化为单径信道模型。时延扩展很小说明传输距离较近（也可以解释径的数量较少）、K因子很大说明是LOS场景，LOS场景下通信以LOS径进行通信，LOS径占了90%甚至95%~98%的功率。虽然有其他一些径的存在，但是功率太小不可能进行通信。不过如果是论文中严谨一些，建议采用TR 38.901中的信道模型，目前全球通信公司预研基本都用的该模型，具有代表性。from this link

其他毫米波信道建议采用：3GPP TR 38.901

毫米波相关论文最常使用的毫米波信道模型都是基于Saleh-Valenzuela模型，包含一堆方位角、俯仰角之类。毫米波绕射能力差，路径稀疏，信道模型具有丰富的几何特征。
以下引用作者原话：

毫米波信道与低频信道不同，由于毫米波基本沿直线传播，绕射能力差，其信道的散射路径较少，往往远少于发射和接收天线的数量，因此其信道模型具有丰富的几何特征。而低频信道由于散射路径丰富，往往建模成随机信道比如瑞利分布，因此并不包含通信环境的信息。

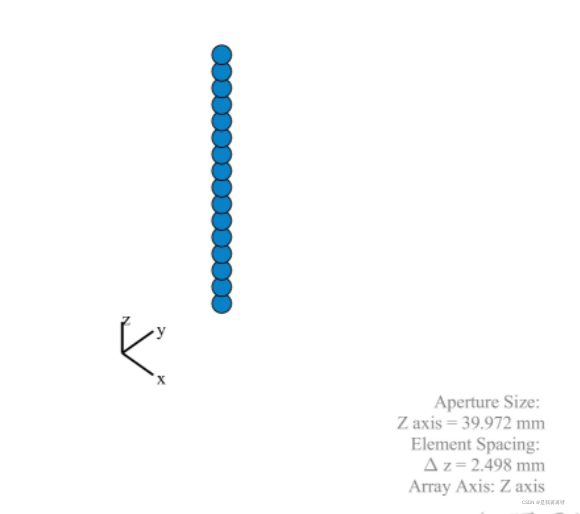
均匀线性阵列（Uniform Linear Array, ULA）

2D MIMO 通信系统发射天线是线性天线，它形成的波束较宽，只有水平维度的方向，没有垂直维度的方向。这样每条子径包含发射端的出发角 AoD（Angle of Departure），接收端的到达角 AoA（Angle of Arrival）以及 时延 三个特征变量。

均匀平面阵列（Uniform Planar Array, UPA）

3D MIMO 通信系统一般在基站端配备大规模的均匀平面天线阵列 。3D MIMO 通信系统基站端配备的天线元件多，且相对于 2D MIMO 通信系统新增加了垂直方向的天线自由度，即系统可以同时在水平维和垂直维上灵活精确调整波束方向，这样发射端可以形成更窄、更精确的波束，具有很高的指向性。 此时描述子径的应该是 离开和到达的方位角 (azimuth angle)，仰角 (elevation angle)。

毫米波信道模型

发射端和接收端均为 ULA

考虑简单模型，没有 cluster，假设只有 $L$ 条散射路径。
经典的 Saleh-Valenzuela (S-V) 信道模型，假设发射天线有 $N_t$ 根，接收天线有 $N_r$ 根，则 $L$ 条散射路径的归一化窄带毫米波信道可以表示为：
$$H=\sqrt{\frac{N_t{N}_r}{L}}\sum _{\ell =1}^L{\alpha }_{\ell }{\mathbf{a}}_r(v_{\ell }){\mathbf{a}}_t^H({\varphi }_{\ell })$$

• ${\alpha }_{\ell }$ 代表第 $\ell$ 条路径的衰落系数，一般建模为高斯分布。
• $v_{\ell }$ 和 ${\varphi }_{\ell }$ 分别是第 $\ell$ 条路径的到达角 AoA 和出发角 AoD，一般简化假设在 $[-\frac{\pi }{2},\frac{\pi }{2}]$ 内均匀分布, 可以根据参考文献决定范围。
• $\mathbf{a}(\theta )$ 是天线阵列的方向矢量(steering vector)，又称为 array response，当天线为 N 维 ULA 时，归一化的方向矢量表达式为
  $${\mathbf{a}}_{ULA}(\theta )=\frac{1}{\sqrt{N}}[1,e^{j\frac{2\pi }{\lambda }d\sin (\theta )},\cdots ,e^{j\frac{2\pi }{\lambda }d(N-1)\sin (\theta )}{]}^T$$ ${\mathbf{a}}_r(v_{\ell })$ 表示的是第 $\ell$ 径接收端的方向矢量，是 $N_r\times 1$ 维的向量; ${\mathbf{a}}_t^H({\varphi }_{\ell })$ 表示第 $\ell$ 径的发射端的方向矢量，是 $N_t\times 1$ 维的向量; ${\mathbf{a}}_r(v_{\ell }){\mathbf{a}}_t^H({\varphi }_{\ell })$ 是 $N_r\times N_t$ 维的矩阵; 把这些所有 $L$ 条路径相加，也就是我们的信道矩阵。

MIMO信道收发端都是 ULA天线阵列的时候，steering vector如上所示，但对于 MISO (SIMO) 模型，接收端（发射端）只有一个天线的话应该就不用考虑接收端（发射端）的方向矢量了。

发射端和接收端均为 UPA

假设有 $N_{cl}$ 个散射簇，每个散射簇中包含 $N_{ray}$ 条传播路径。窄带毫米波信道表示为：$$H=\sqrt{\frac{N_t{N}_r}{N_{cl}{N}_{ray}}}\sum _{i=1}^{N_{cl}}\sum _{\ell =1}^{N_{ray}}{\alpha }_{i\ell }{\mathbf{a}}_r({\varphi }_{i\ell }^r,{\theta }_{i\ell }^r){\mathbf{a}}_t^H({\varphi }_{i\ell }^t,{\theta }_{i\ell }^t)$$

• ${\alpha }_{i\ell }$ 代表第 $i $个散射簇中第 $\ell$ 条路径的衰落系数。
• ${\varphi }_{i\ell }^r,{\theta }_{i\ell }^r$ 代表接收端的方向角和俯仰角。${\mathbf{a}}_r({\varphi }_{i\ell }^r,{\theta }_{i\ell }^r)$ 表示方向角和俯仰角在接收端的归一化天线阵列响应向量。
• ${\mathbf{a}}_t^H({\varphi }_{i\ell }^t,{\theta }_{i\ell }^t)$ 代表发射端的方向角和俯仰角，${\mathbf{a}}_t^H({\varphi }_{i\ell }^t,{\theta }_{i\ell }^t)$ 表示方向角和俯仰角在发射端的归一化天线阵列响应向量。
• 针对该图 UPA放置在 X-Z 平面上的情形，发射端 UPA天线阵列的归一化响应向量可以表示为：
  $$\begin{gathered} {\mathbf{a}}_{ULA}(\varphi ,\theta )=\sqrt{\frac{1}{N}}[1,\cdots ,e^{j\frac{2\pi }{\lambda }d[m\sin (\varphi )\sin (\theta )+n\cos (\theta )]},\cdots , \\ {e}^{j\frac{2\pi }{\lambda }d[(N_x-1)\sin (\varphi )\sin (\theta )+(N_z-1)\cos (\theta )]}{]}^T \end{gathered}$$
  $N$ 为均匀平面阵列的天线元素个数，x 轴和 z 轴上分别有 $N_x$ 和 $N_z$ 个天线元素，$d$ 是天线间隔。该表达式还可以写为克罗内克积的形式，更简洁。
  注意，该公式的 $\varphi$ 表示的即为图中表示的 TX 端的俯仰角。针对UPA来说，steering vector 和俯仰角的关系取决于UPA的在三维坐标中的放置，下面给出 UPA 放置在Y-Z平面 和 X-Y平面的两种情形。
• Y-Z平面放置IRS的情形
• X-Y平面放置IRS的情形
  UAV 端的 UPA 天线阵列的归一化响应向量 [5] 可以表示为：
  $$\begin{gathered} {\mathbf{a}}_{ULA}({\varphi }_{k,\ell }^n,{\theta }_{k,\ell }^n)=\sqrt{\frac{1}{M_E{N}_A}}[1,\cdots ,e^{j\frac{2\pi }{\lambda }[m{d}_x\sin ({\theta }_{k,\ell }^n)\cos ({\varphi }_{k,\ell }^n)+n{d}_y\sin ({\theta }_{k,\ell }^n)\sin ({\varphi }_{k,\ell }^n)]},\cdots , \\ {e}^{j\frac{2\pi }{\lambda }[(N_A-1)d_x\sin ({\theta }_{k,\ell }^n)\cos ({\varphi }_{k,\ell }^n)+(M_E-1)d_y\sin ({\theta }_{k,\ell }^n)\sin ({\varphi }_{k,\ell }^n)]}{]}^T \end{gathered}$$
  $d_x$ 和 $d_y$ 分别表示X和Y轴上的天线之间的间距，一般取 $d=\frac{\lambda }{2}$ 。
  ${\varphi }_{k,\ell }^n$ 和 ${\theta }_{k,\ell }^n$ 分别表示方向角和方位角, 定义如图 Fig.2 所示。我们定义第 $n$ 个 UAV 的位置为 $(x_n,y_x,z_n)$，面向第 $k$ 个 UE 的第 $\ell$ 条径的散射体的位置为 $(x_k^{\ell },y_k^{\ell },0)$，那么 ${\varphi }_{k,\ell }^n$ 和 ${\theta }_{k,\ell }^n$ 表达式如下：
  $$\begin{gathered} {\theta }_{k,\ell }^n=\arctan \left(\frac{\sqrt{(x_k^{\ell }-x_n{)}^2+y_k^{\ell }-y_n{)}^2}}{z_n}\right) \\ {\varphi }_{k,\ell }^n=\arctan \left(\frac{y_k^{\ell }-y_n}{x_k^{\ell }-x_n}\right)-\pi \min (\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(x_k^{\ell }-x_n),0) \end{gathered}$$
  其中，$\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}$为符号函数: $x>0$, $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(x)=1$; $x=0$, $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(x)=0$; $x<0$, $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(x)=-1$。
  
• 注意，这里的 $N_{ray}$ 条传播路径包含 1条 LoS 路径，以及 $(N_{ray}-1)$ 条 NLoS 路径。在 UAV-UE 之间不存在遮挡的情形，只有一条 LoS 径，没有簇和散射径，将 $N_r=1,N_{cl}=1,N_{ray}=1$ 带入 $H$ 得到：
  $$h_k^n=\sqrt{N_t}{\alpha }_k^n{\mathbf{a}}_t({\theta }_k^n,{\varphi }_k^n)$$
  ${\alpha }_k^n$ 为第 $n$ 个 UAV 和第 $k$ 个 UE 之间的LoS径的信道增益系数。非遮挡情况（即 LoS 径）的概率是关于仰角 ${\xi }_k^n=\arctan (\frac{z_n}{D_k})$ 的一个函数，$D_k$ 为第 $n$ 个 UAV 和第 $k$ 个 UE 之间的距离；该概率会随着仰角的增大而增大，当 $z_n$ 足够大时，LoS 径的概率趋于1。该概率表达式为：
  $$P_{No-blockage}=\frac{1}{1+a{e}^{(-b({\xi }_k^n-a))}}$$
  ${\xi }_k^n=\arctan (\frac{z_n}{D_k})$是仰角；$a,b$ 是取决于信道环境（e.g., rural, urban, or dense urban）的正的模型参数。遮挡概率为 $P_{Blockage}=1-P_{No-blockage}$.

存在 IRS 的情况

• 当在发射端和接收端存在 IRS 时，就看假设 IRS 搭载的是 ULA 还是 UPA，然后带入相应的 steering vector 计算窄带毫米波信道增益即可。

S-V 毫米波信道仿真

仿真参数

在论文仿真中一般假设 ${\alpha }_{i\ell }$ 信道增益系数服从0均值的复高斯随机分布，对于存在blockage和不存在blockage的场景，方差的设定不同，可以参考文献仿真部分的参数设定，比如：

• ${\alpha }_{i\ell }\sim \mathcal{C}\mathcal{N}(0,10^{-0.1{\mathrm{P}}_{\mathrm{L}}})$, where the distance-dependent path loss is modeled as $${\mathrm{P}}_{\mathrm{L}}({\mathrm{d}}_{\mathrm{\ell }})=\alpha +10\beta {\log }_{10}(d_{\ell })+{\xi }_{\ell }$$
  $d_{\ell }$为第$\ell$条径的收发端距离，$\alpha ,\beta$ 为常数，${\xi }_{\ell }\sim \mathcal{N}(0,{\sigma }^2)$。
  对 $H_{\ell }$ 的 LoS 径 (non-blockage)，$\alpha =61.4,\beta =2,\sigma =5.8$ dB；
  对 $H_{\ell }$ 的 NLoS 径 (blockage)，$\alpha =72.0,\beta =2.92,\sigma =8.7$ dB [5, 6] 。
• 毫米波载波频率设为 28 GHz [5-ref 36/37]，带宽 251.1886 MHz [4]。
• 信道环境参数 (计算 LoS 概率) $a=11.95,b=0.14$。 [5-ref36]
• 天线间距 $d=\frac{\lambda }{2}$。
• 噪声功率 ${\sigma }^2=-91$ dBm [6] 或 ${\sigma }^2=-174+10{\log }_{10}B=-90$ dBm [4]。

仿真实例

System Model

• IRS系统可以分为三个信道：

1. 基站直接到达用户的信道： BS-UE 信道
2. 基站到智能反射面的信道： BS-IRS 信道
3. 智能反射面到用户的信道：IRS-UE 信道

• steering vector
  

Matlab Codes

• 实现单侧UPA的天线响应向量的仿真函数

function y = array_response(phi,theta, N)  
for m= 0:sqrt(N)-1     % IRS is square array (N elements)
    for n= 0:sqrt(N)-1
        y(m*(sqrt(N))+n+1) = exp( 1i* pi* ( m*sin(phi)*sin(theta) + n*cos(theta) ) ); % i represents complex 
    end
end
y = y.'/sqrt(N); 		% normalized
end

• BS-IRS 信道生成函数 （IRS - UE的信道生成同理）

function H = generate_channel(Nt, Nr, L)
	AoD = pi*rand(L, 2) - pi/2;  % -2/pi~2/pi (generating the angles of departure for L paths)
	AOA = pi*rand(L, 2) - pi/2;  % -2/pi~2/pi (generating the angles of arrival for L paths)
	alpha(1) = 1; 				 % gain of the LoS
	alpha(2:L) = 10^(-0.5)*(randn(1,L-1)+1i*randn(1,L-1))/sqrt(2);  % gains of the NLoS
	H = zeros(Nr, Nt);
for l=1:1:L
    ar = array_response(AOA(L,1),AOA(L,2), Nr);
    at = array_response(AOD(L,1),AOD(L,2), Nt);
    H = H + sqrt(Nr * Nt)*alpha(l)*ar*at';
end

• Note: 需要指出实际中方位角和仰角的变化范围应该不同，仰角的变化范围会偏小， 因此更合理的仿真应该进一步限制其生成范围。 但就像上面所说，如果只是为了随机生成智能反射面信道用于仿真，不用纠结的那么细。
• alpha 代表的是信道的衰落系数， 为了区别LOS径和NLOS径，我们默认第一径是LOS径，给了归一化的能量为1。 而NLOS径的能量则是高斯变量， 并且为了体现出与LOS径的能量差， 给了一个衰减系数。
• 关于该场景 BS-UE 的信道， 有几种不同的建模：

1. 直接假设BS-UE间被阻隔， 即不存在LoS径，但是有NLOS径，那么就可以用上面的代码去仿真，只需要把 LOS 径去掉即可。
2. 假设为瑞利衰落信道（许多论文采用这个建模），瑞利的仿真代码非常容易， 网上查找，不再赘述。

来自作者的 Remark

1. 在仿真中衰落系数设定时，只要衰落取值有据可循，能体现距离导致的衰落即可。
2. 路径较少，稀疏信道用SV，路径太多又不想逐一建模，简单起见用瑞丽建模。
3. 建模信道的时候已经体现了， 毫米波的稀疏性等。 至于具体频率这些与LTE的不同，在仿真中其实没有体现。 因为考虑是等效基带的场景，不论是什么射频都等效到基带完成。（待考究）
4. 部分资料里：当天线为全向天线时，方位角范围−π_{π，俯仰角−0.5π}0.5π，当天线是定向天线时，会有定向天线增益。这里只是随机举个例子。比如有时候基站会选择30-150度是水平角范围，30-60是仰角范围。不同场景不一样。你写程序的时候把这个作为变量，甚至可以多跑几种参数。文献的话可以去搜IRS相关的paper，然后看他们选取的信道参数。据我所知都是大同小异，因为这个不是文章的重点。
5. 在这个模型里面的路径总数L设一个3-20的随机整数即可。
6. α 代表的是信道的衰落系数， 为了区别LOS径和NLOS径，我们默认第一径是LOS径，给了归一化的能量为1。 而NLOS径的能量则是高斯变量， 并且为了体现出与LOS径的能量差， 给了一个衰减系数。那么当 IRS 和 UE 之间的距离改变时，是衰落系数α改变还是衰减系数发生改变呢？
   alpha在改变。一般认为衰减系数决定于NLOS所经过的反射体的衰减，这个应该不会随距离变化。如果认为是开阔空间的话，直接按衰落与距离平方成反比，来模拟就行。
7. 实际中衰落因子就是由距离计算而来，但是我们仿真时考虑普遍情况，即不知道用户的具体位置。那么，将衰落因子设置为高斯变量，进行几千次蒙特卡洛仿真，可以视作仿真了用户在各种不同距离 位置的情况。现在一般的仿真都可以这样设置。当然，你也可以设置一个具体的用户位置，计算衰落因子，但这样有失一般性，因为你应当希望估计的算法能适用于所有的信道（对应不同的用户位置）
8. 为什么没有考虑多路径的时延，而是直接将各路径的信道相加呢？
   相比于信号周期，各径延时可以忽略不计，等效看作时同时到达，这就是窄带模型。宽带模型因为信号周期短，因此要考虑时延，但UPA的响应及智能反射面的响应等公式依旧是通用的。考虑的是窄带情形，宽带情形的话是需要考虑时延的，一般按ofdm进行仿真。

Userful code links

https://blog.csdn.net/weixin_39274659/article/details/104434934
code reproduction of an paper
total IRS related code transfer

IRS 综述

reference link

参考文献

[1] Ayach O E , Rajagopal S , Abu-Surra S , et al. Spatially Sparse Precoding in Millimeter Wave MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2013, 13(3):1499-1513.
[2] Akdeniz M R , Liu Y , Samimi M K , et al. Millimeter Wave Channel Modeling and Cellular Capacity Evaluation[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6):1164-1179.
[3] Yu X , Shen J C , Zhang J , et al. Alternating Minimization Algorithms for Hybrid Precoding in Millimeter Wave MIMO Systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(3):485-500.
[4] Wang P , Fang J , Dai L , et al. Joint Transceiver and Large Intelligent Surface Design for Massive MIMO MmWave Systems[J]. IEEE Transactions on Wireless Communications, 2020, PP(99):1-1.
[5] Jiang L , H Jafarkhani. Reconfigurable Intelligent Surface-Assisted mmWave multi-UAV Wireless Cellular Networks[J]. 2021.
[6] Hong S H , Park J , Kim S J , et al. Hybrid Beamforming for Intelligent Reflecting Surface Aided Millimeter Wave MIMO Systems[J]. 2021.