关键词:稀土化合物;DFT,Gaussian,量子化学,结构优化
稀土化合物是指含有稀土元素(镧系元素和钇)的化合物,因其独特的电子结构和化学性质,在催化、光电、磁性、电子、能源等多个领域有着广泛应用。稀土元素具有优异的光学、电学、磁学性能,能够用于制造高效的永磁材料、荧光材料、催化剂、激光介质以及高温超导材料等。通过各种先进的合成方法,可以调控稀土化合物的物理化学性质,以满足不同应用需求,它们在新材料、清洁能源以及高科技领域的潜力日益凸显。
密度泛函理论(DFT)的计算方法,由于其良好的计算效率和准确度,被广泛应用于稀土化合物的电子结构研究、光学性能、磁性以及催化性能等领域。在这一过程中,Gaussian软件作为一种经典的量子化学计算程序,提供了丰富的功能来支持DFT计算,广泛应用于稀土化合物的研究。
在稀土化合物的研究中,Gaussian软件结合密度泛函理论(DFT)能够在多个方面提供关键的理论支持。首先,通过DFT计算可以优化稀土化合物的几何结构,获得最低能量构型,从而帮助确定金属中心的配位数和几何构型,分析化合物的稳定性。其次,Gaussian能够精确计算稀土化合物的电子结构,揭示电子轨道分布和f电子的贡献,为理解其光学性质(如吸收光谱、发光特性)和磁性(如磁矩、磁各向异性)提供重要信息。此外,Gaussian还可用于研究催化反应的反应机理,计算过渡态和活化能,进而为稀土化合物在催化领域的应用提供理论指导。最后,通过计算振动频率、NMR、IR和UV-Vis光谱,Gaussian能够预测稀土化合物的光谱特性,这对于研究其在光电材料、荧光材料和激光器中的应用具有重要价值。总体而言,Gaussian与DFT方法为稀土化合物的结构、性质与应用研究提供了全面的理论支持。
在使用Gaussian进行稀土金属化合物结构优化时,主要面临以下几个困难和挑战:
-
f电子的处理:稀土金属化合物中通常包含f区电子,而f电子的处理非常复杂。Gaussian采用DFT方法时,常常需要选择合适的交换-关联泛函(如LDA、GGA或混合泛函),但是传统的DFT方法可能无法精确描述f电子的局部化特性或强电子相关效应,这可能导致优化结果与实验观察之间存在差异。针对这一问题,可能需要采用更加精细的计算方法(如DFT+U或多体方法)来更好地描述f电子。
-
强电子相关效应:稀土金属常常表现出强烈的电子相关效应,尤其是在过渡金属和稀土金属的配合物中,金属中心的价电子与配体之间的相互作用非常复杂。标准的DFT方法可能无法完全捕捉这些相关效应,从而影响结构优化的精确度。为了解决这一问题,通常需要引入如 Hubbard U修正等方法来改进描述。
-
复杂的几何构型:稀土金属化合物的几何构型可能非常复杂,尤其是在大配位数(如8配位或以上)或多核体系中。优化这样复杂的结构时,容易遇到局部最小值的问题,优化过程可能会陷入某些非真实的稳定构型。因此,优化时常常需要较高的精度和细致的初始化结构。
-
基组选择和收敛问题:在计算稀土金属化合物时,选择合适的基组非常重要。尤其是在涉及到较大原子(如稀土元素)的化合物时,常规的小基组可能无法提供足够的准确性。为了提高计算精度,通常需要使用较大且适合金属体系的基组。此外,在几何优化过程中,可能会遇到收敛困难,尤其是在涉及到低对称性或多个能量水平相近的情况时。
-
多电子效应与自旋极化:稀土金属化合物可能具有较为复杂的自旋态或多重电子态(如高自旋态、低自旋态的转换)。Gaussian在处理这些自旋态变化时可能会遇到困难,尤其是在进行结构优化时,需要特别注意选择合适的自旋态和计算设置。
总的来说,使用Gaussian进行稀土金属化合物结构优化时,主要会遇到l502报错,SCF收敛失败。判断自旋多重度时需要更多的考虑,SCF收敛性更难,主要因为d轨道接近简并,还容易收敛到不稳定的波函数。镧系和锕系配合物的计算更复杂,因为f轨道的近简并导致SCF比过渡金属配合物更难收敛(除非使用大核赝势,不再考虑f电子)。因此,检查波函数稳定性非常重要,而且这些化合物通常有更高的配位数,结构也更复杂。
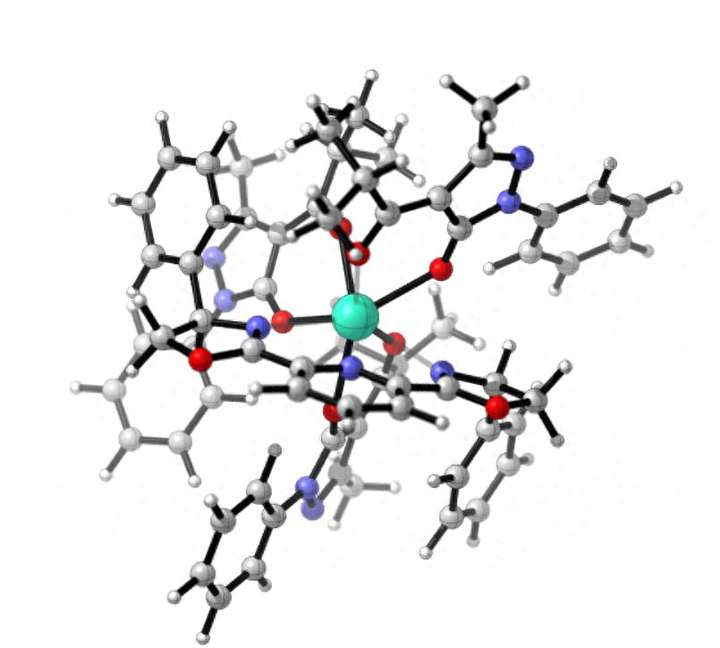
图1 Tb(III)化合物结构
如图1,Tb(III)化合物作为要计算的例子,在剑桥结构数据库(CSD)里面导出该化合物晶体结构,即cif分子坐标。进行稀土化合物结构优化时,自旋多重度的设置非常重要!Tb稀土金属的核外价电子结构为4f96s2。该配合物的自旋多重度取决于Tb(III)中心的8个4f电子的排布,可能为七重态、七重态、三重态或单重态。在进行几何优化和振动分析时,我们采用大核赝势进行计算,这样4f电子被赝化处理。因此,Tb(III)中心的价电子仅包括占据5s和5p轨道的8个电子,而配体部分则为闭壳层结构。基于这一点,在计算时应假设配合物为单重态。
PBE0是一个非常值得优先选择的交换-关联泛函,已经在许多研究中用于镧系配合物的计算。例如,2019年发表在《Inorg. Chem.》上的一篇文章(58, 411)中,研究者采用PBE0结合SDD赝势对含Pr的体系进行了计算。因此笔者也推荐使用PBE0交换-关联泛函进行稀土化合物的结构优化。
Gaussian软件内置了五种Stuttgart赝势用于Tb元素的计算,分别是ECP28MHF,ECP28MWB,ECP53MWB,ECP54MHF,ECP54MWB,ECP55MHF和ECP55MWB。其中,MHF系列赝势不适用于大多数计算,因为它们在拟合时没有考虑相对论效应,导致结果不准确,例如配位键的键长明显不合理。
MWB28赝势是采用Wood-Boring方法考虑准相对论效应的小核赝势,替代了Tb的28个内层电子(包括1s、2s、2p、3s、3p和3d电子)。MWB54和MWB55是大核赝势,分别替代了Tb的54个内层电子(包括1s、2s、2p、3s、3p、3d、4s、4p、4d和4f电子)。其中,MWB54专门用于Tb(III),该状态下Tb失去了2个6s电子和1个4f电子,因此共54个电子被赝化。MWB55则专门用于Ho(II)。
使用大核赝势的优势在于,它简化了计算,特别是在配合物中近简并的4f轨道不需要被精确描述时,SCF收敛更为顺利,并且计算速度相较于小核赝势更快。然而,大核赝势的精度通常不如小核赝势,并且其可移植性较差,因此不适合用于研究配位变化较大的反应过程(例如涉及配位键形成和断裂、异构化等)。此外,使用大核赝势时,研究者需要自行判断原子的价态。Stuttgart赝势在Institute for Theoretical Chemistry下载。Tb(III)化合物优化的输入文件关键词“#p opt genecp em=gd3bj pbe1pbe”。
由于镧系锕系配合物容易收敛到不稳定波函数,因此加上stable=opt,使得程序对SCF收敛后的波函数进行检测,如果不稳定的话则自动试图优化到稳定波函数。结构优化顺利结束后,导出最后一帧分子结构,加关键词#p PBE1PBE/genecp em=gd3bj int=fine stable=opt进行波函数稳定性优化。输出“The wavefunction is stable under the perturbations considered.”即波函数稳定了。最终chk文件里记录的就是稳定的波函数了。
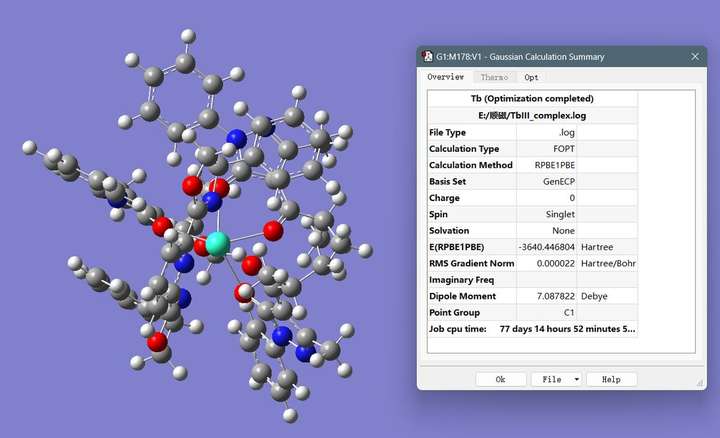
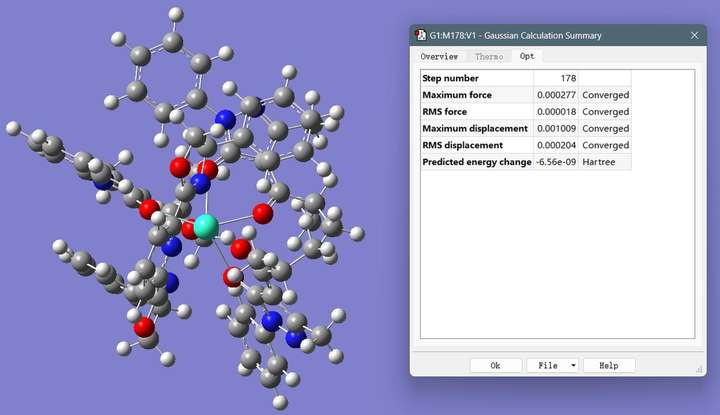
图2 结构优化结果
最后,有相关需求欢迎通过公众号“320科技工作室”与我们联络。

























 1157
1157

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










