iSAM论文解读

iSAM论文解读

Abstract

• 提出了增量式平滑建图(iSAM)
• 基于快速增量矩阵分解
• 只需要重新计算实际变化的矩阵项
• 对于具有很多回环的轨迹也有效
• 数据实时关联
• 对iSAM各个组成部分进行评估
  
  

Ⅰ. INTRODUCTION

• SLAM要求实时。大规模环境，在线数据关联，目前还没有工作同时满足这一要求（2008）
• previours work——SAM：新的测量值可用时，先更新信息矩阵，然后将其分解
• iSAM：直接用新的测量值更新平方根信息矩阵，只需要对实际受新观测值影响的项进行计算
• 带有循环的轨迹：周期性重排序可以减小不必要的填充
• 在线数据关联：避免计算整个协方差矩阵，提出了更快速的保守估计和精确估计两种方法
• 在数据集上进行了评估，结果表明iSAM提供了有效和精确的解决方案
  
  

Ⅱ. SAM: A SMOOTHING APPROACH TO SLAM

A. A Probabilistic Model for SLAM

如图所示，SLAM问题可以转化为贝叶斯置信网络，其中 X = { x i } X=\left\{\mathbf{x}_i\right\} X={xi​}表示状态量， L = { l j } L=\left\{\mathbf{l}_j\right\} L={lj​}表示地标， U = { u i } U=\left\{\mathbf{u}_i\right\} U={ui​}表示控制输入量， Z = { z k } Z=\left\{\mathbf{z}_k\right\} Z={zk​}表示地标的观测量。所有变量和观测的概率分布：
$$P(X,L,U,Z)\propto P\left({\mathbf{x}}_0\right)\prod _{i=1}^{M}P\left({\mathbf{x}}_i\mid {\mathbf{x}}_{i-1},{\mathbf{u}}_i\right)\prod _{k=1}^{K}P\left({\mathbf{z}}_k\mid {\mathbf{x}}_{i_k},1_{j_k}\right)\text{\hspace{1em}(1)}$$
其中$P\left({\mathbf{x}}_0\right)$是初始状态的先验，$P\left({\mathbf{x}}_i\mid {\mathbf{x}}_{i-1},{\mathbf{u}}_i\right)$是运动模型，$P\left({\mathbf{z}}_k\mid {\mathbf{x}}_{i_k},{\mathbf{l}}_{j_k}\right)$是观测模型。

假设测量是高斯的，则运动模型：
$${\mathbf{x}}_i=f_i\left({\mathbf{x}}_{i-1},{\mathbf{u}}_i\right)+{\mathbf{w}}_i\text{\hspace{1em}(2)}$$
运动模型可以通过里程计传感器或扫描匹配获得，${\mathbf{w}}_i$是零均值的正态噪声，协方差矩阵为${\Lambda }_i$。
观测模型：
$${\mathbf{z}}_k=h_k\left({\mathbf{x}}_{i_k},{\mathbf{l}}_{j_k}\right)+{\mathbf{v}}_k\text{\hspace{1em}(3)}$$
${\mathbf{v}}_k$是零均值的正态测量噪声，协方差矩阵为${\Gamma }_k$。

B. SLAM as a Least Squares Problem

将问题转换为基于最大后验估计（MAP）的最小二乘问题，即给定输入U和地标测量Z，求最优的轨迹和地图的估计$X^{\ast },L^{\ast }$：
$$\begin{array}{rl}{X}^{\ast },L^{\ast }& =\arg \underset{X,L}{\max }P(X,L,U,Z)\\ & =\arg \underset{X,L}{\min }-\log P(X,L,U,Z)\end{array}\text{\hspace{1em}(4)}$$
这里取负对数是为了把高斯分布的概率密度函数转换乘最小二乘的形式：
$$\begin{array}{rl}{X}^{\ast },L^{\ast }=\arg \underset{X,L}{\min }& \{\sum _{i=1}^M{\Vert f_i\left({\mathbf{x}}_{i-1},{\mathbf{u}}_i\right)-{\mathbf{x}}_i\Vert }_{{\Lambda }_i}^2+\sum _{k=1}^K{\Vert h_k\left({\mathbf{x}}_{i_k},{\mathbf{l}}_{j_k}\right)-{\mathbf{z}}_k\Vert }_{{\Gamma }_k}^2\}\end{array}\text{\hspace{1em}(5)}$$
这个公式是SLAM经典的最小二乘问题，和其它例如FAST-LIO论文，SLAM十四讲中的描述是一致的。如果f和h是非线性的，可以采用GN或LM算法求解，这类似于EKF的思想。

接下来将这个公式简化。首先通过泰勒展开：
$$\begin{array}{rl}& f_i\left({\mathbf{x}}_{i-1},{\mathbf{u}}_i\right)-{\mathbf{x}}_i\\ \approx & \left\{f_i\left({\mathbf{x}}_{i-1}^0,{\mathbf{u}}_i\right)+F_i^{i-1}\delta {\mathbf{x}}_{i-1}\right\}-\left\{{\mathbf{x}}_i^0+\delta {\mathbf{x}}_i\right\}\\ =& \left\{F_i^{i-1}\delta {\mathbf{x}}_{i-1}-\delta {\mathbf{x}}_i\right\}-{\mathbf{a}}_i\end{array}$$
其中$F_i^{i-1}$是$f_i(.)$在线性化点${\mathbf{x}}_{i-1}^0$处的雅可比矩阵：
$$F_i^{i-1}:={\frac{\partial f_i\left({\mathbf{x}}_{i-1},{\mathbf{u}}_i\right)}{\partial {\mathbf{x}}_{i-1}}|}_{{\mathbf{x}}_{i-1}^0}$$

${\mathbf{a}}_i:={\mathbf{x}}_i^0-f_i\left({\mathbf{x}}_{i-1}^0,{\mathbf{u}}_i\right)$是里程计的预测误差。对测量方程同理：
$$\begin{array}{rl}& h_k\left({\mathbf{x}}_{i_k},{\mathbf{l}}_{j_k}\right)-{\mathbf{z}}_k\\ \approx & \left\{h_k\left({\mathbf{x}}_{i_k}^0,{\mathbf{l}}_{j_k}^0\right)+H_k^{i_k}\delta {\mathbf{x}}_{i_k}+J_k^{j_k}\delta {\mathbf{l}}_{j_k}\right\}-{\mathbf{z}}_k\\ =& \left\{H_k^{i_k}\delta {\mathbf{x}}_{i_k}+J_k^{j_k}\delta {\mathbf{l}}_{j_k}\right\}-{\mathbf{c}}_k\end{array}$$
其中$H_k^{i_k}$和$$J_k^{j_k}$分别是测量函数$h_k(.)$在线性化点$\left({\mathbf{x}}_{i_k}^0,1_{j_k}^0\right)$处关于${\mathbf{x}}_{i_k}$和${\mathbf{l}}_{j_k}$的雅可比矩阵：

$$H_k^{i_k}:={\frac{\partial h_k\left({\mathbf{x}}_{i_k},{\mathbf{l}}_{j_k}\right)}{\partial {\mathbf{x}}_{i_k}}|}_{\left({\mathbf{x}}_{i_k}^0,{\mathbf{l}}_{j_k}^0\right)}$$
$$J_k^{j_k}:={\frac{\partial h_k\left({\mathbf{x}}_{i_k},{\mathbf{l}}_{j_k}\right)}{\partial {\mathbf{l}}_{j_k}}|}_{\left({\mathbf{x}}_{i_k}^0,{\mathbf{l}}_{j_k}^0\right)}$$
其中${\mathbf{c}}_k:={\mathbf{z}}_k-h_k\left({\mathbf{x}}_{i_k}^0,{\mathbf{l}}_{j_k}^0\right)$是测量预测误差。将上式代入：
$$\begin{array}{rl}& \delta {\mathbf{\theta }}^{\ast }=\arg \underset{\delta \mathbf{\theta }}{\min }\{\sum _{i=1}^M{\Vert F_i^{i-1}\delta {\mathbf{x}}_{i-1}+G_i^i\delta {\mathbf{x}}_i-{\mathbf{a}}_i\Vert }_{{\Lambda }_i}^2+\sum _{k=1}^K{\Vert H_k^{i_k}\delta {\mathbf{x}}_{i_k}+J_k^{j_k}\delta {\mathbf{l}}_{j_k}-{\mathbf{c}}_k\Vert }_{{\Gamma }_k}^2\}\\ & \end{array}$$

其中$\mathbf{\theta }\in {\mathbb{R}}^n$是包含所有位姿和地标变量。上式表明我们的问题转换成了一个线性的最小二乘问题，其中$G_i^i$是单位阵。
接下来为了简化，通过以下方法去掉协方差矩阵。以协方差矩阵$\Lambda$为例，令${\Lambda }^{-1/2}$为$\Lambda$的平方根，令$e$为误差变量，则：
$$\Vert \mathbf{e}{\Vert }_{\Lambda }^2:={\mathbf{e}}^T{\Lambda }^{-1}\mathbf{e}={\left({\Lambda }^{-T/2}\mathbf{e}\right)}^T\left({\Lambda }^{-T/2}\mathbf{e}\right)={\Vert {\Lambda }^{-T/2}\mathbf{e}\Vert }^2$$
因此我们可以在$F_i^{i-1},G_i^i$和${\mathbf{a}}_i$中每一项预先乘一个 ${\Lambda }_i^{-T/2}$来消除${\Lambda }_i$,而${\Gamma }_k$同理。

最后，把雅可比矩阵整理成一个大矩阵$A$，把${\mathbf{a}}_i$和${\mathbf{c}}_k$整理到一个向量$b$，则问题转换为：
$$\delta {\mathbf{\theta }}^{\ast }=\arg \underset{\delta \mathbf{\theta }}{\min }\Vert A\delta \mathbf{\theta }-\mathbf{b}{\Vert }^2\text{\hspace{1em}(6)}$$

其中$A\in {\mathbb{R}}^{m\times n}$是一个大而稀疏的雅可比矩阵，$b\in {\mathbb{R}}^m$测量向量，论文中又叫做right-hand side (RHS) 向量。这样的问题显然可以通过方程$A^{T}A\mathbf{\theta }=A^{T}b$求解。

C. Solving by QR Factorization

应用标准的QR分解来分解测量雅可比矩阵A：
$$A=Q\left[\begin{array}{l}R\\ 0\end{array}\right]\text{\hspace{1em}(7)}$$
其中$R\in {\mathbb{R}}^{n\times n}$是上三角的平方根信息矩阵，$Q\in {\mathbb{R}}^{m\times m}$是正交矩阵。代入到式(6)：
$$\begin{array}{rl}\Vert A\mathbf{\theta }-\mathbf{b}{\Vert }^2& ={\Vert Q\left[\begin{array}{c}R\\ 0\end{array}\right]\mathbf{\theta }-\mathbf{b}\Vert }^2\\ & ={\Vert Q^{T}Q\left[\begin{array}{c}R\\ 0\end{array}\right]\mathbf{\theta }-Q^T\mathbf{b}\Vert }^2\\ & ={\Vert \left[\begin{array}{c}R\\ 0\end{array}\right]\mathbf{\theta }-\left[\begin{array}{c}\mathbf{d}\\ \mathbf{e}\end{array}\right]\Vert }^2\\ & =\Vert R\mathbf{\theta }-\mathbf{d}{\Vert }^2+\Vert \mathbf{e}{\Vert }^2\end{array}\text{\hspace{1em}(8)}$$
其中定义$[\mathbf{d},{\mathbf{e}}^T]:=Q^T\mathbf{b}$ 且 $\mathbf{d}\in {\mathbb{R}}^n$，$\mathbf{e}\in {\mathbb{R}}^{m-n}$。当$R\mathbf{\theta }=d$时式(8)最小，因此QR分解将最小二乘问题简化为具有唯一解的线性方程：
$$R{\mathbf{\theta }}^{\ast }=\mathbf{d}\text{\hspace{1em}(9)}$$
由于$R$矩阵是上三角矩阵，该方程求解较简单，因此该问题的主要工作在于如何求解矩阵$R$。

Ⅲ. ISAM: INCREMENTAL SMOOTHING AND MAPPING

提出了增量平滑建图，通过在新的测量到达时直接更新平方根因子，来避免不必要的计算量。

A. Matrix Factorization by Givens Rotations

获得矩阵A的QR分解的其中一种方法是使用吉文斯旋转(Givens rotations)变换，它不是矩阵QR分解的首选方法，但它很容易扩展到分解的更新。Givens变换是一种正交变换，它的旋转矩阵为：
$${\mathbf{R}}_{\mathrm{ij}}=\left[\begin{array}{ccccccccccc}1& & & & & & & & & & \\ & \ddots & & & & & & & & & \\ & & 1& & & & & & & & \\ & & & \mathrm{c}& 0& \cdots & 0& \mathrm{s}& & & \\ & & & 0& 1& \cdots & 0& 0& & & \\ & & & ⋮& ⋮& & ⋮& ⋮& & & \\ & & & 0& 0& \cdots & 1& 0& & & \\ & & & -\mathrm{s}& 0& \cdots & 0& \mathrm{c}& & & \\ & & & & & & & & 1& & \\ & & & & & & & & & & 1\end{array}\right].$$

其中$c^2+s^2=1$。如下图所示，改变$c$和$s$的值，矩阵左乘Givens变换矩阵可以使图中的x变成0，且只改变矩阵中红色的部分。如果我们按列来消除矩阵中的非零元素（从第1列第2个元素开始，再到第1列第3个…），就可以把矩阵转换成上三角的形式。而正交旋转矩阵Q通常是密集的，在实践中通常不会直接计算它，可以通过对向量$b$应用同样的Givens变换即可。

B. Incremental Updating

当得到了新的测量值时，通过QR更新来直接修改之前的因子分解是更高效的，而不是直接重新生成矩阵$A$，具体解释如下。

我们假设当得到新的测量时，矩阵变为了$A^{\prime }$(未变换)，我们对它做相同于$A$的Givens变换：
$$\left[\begin{array}{ll}{Q}^T& \\ & 1\end{array}\right]\left[\begin{array}{c}A\\ {\mathbf{w}}^T\end{array}\right]=\left[\begin{array}{c}R\\ {\mathbf{w}}^T\end{array}\right]\text{, }{A}^{\prime }=\left[\begin{array}{c}A\\ {\mathbf{w}}^T\end{array}\right]\text{, new rhs: }\left[\begin{array}{l}\mathbf{d}\\ \gamma \end{array}\right]$$
其中${\mathbf{w}}^T$是新的测量行，$\gamma$是新的RHS向量。可以看出对$A^{\prime }$做Givens变换并不会影响新的测量行。也就是说，当新的测量来临时，我们可以直接把${\mathbf{w}}^T$加到矩阵$A$的下方，RHS向量同理；然后同样利用Givens变换，把新加入的测量行消除成上三角的形式即可。这样的好处是矩阵$A$的大部分元素都不需要变化。如图所示，蓝色的部分是不需要变动的元素，红色则是需要变动。可以看出，当t=50时，由于新加入的测量行通常只与最近的状态量和观测有关，因此新测量行通常是稀疏的，因此只需要通过Givens变化改变少量的元素即可（如图中绿色虚线内的部分）。

C. Incremental SAM

通过上述的方式即可更新平方根因子，由于一般情况下测量行都是稀疏的，因此通常只有新测量行最右边的部分被填充。

对于线性的勘探任务，仿真结果显示需要添加Givens变换的次数与轨迹的长度无关,如图所示。

因此，添加Givens变换的时间复杂度是$O(1)$，而对于求解方程来说，由于矩阵$R$是上三角矩阵，因此其时间复杂度是$O(n)$。仿真结果显示在10000步后大概需要0.12s。

Ⅳ.LOOPS AND NONLINEAR FUNCTIONS

本节讨论iSAM如何处理机器人轨迹中的闭环，并展示了如何使用周期性变量重新排序来避免不必要的计算复杂度。

A. Loops and Periodic Variable Reordering

如图所示为仿真环境中，机器人轨迹为两次"8"。从图(b)和(d)中可以看出，当第一次回环（A）时，矩阵$R$显然出现了一些填充；当第二次回环(B)时，矩阵$R$的填充十分显著，第三次回环（C）时更甚。且在三次回环时，计算量也明显地增加。

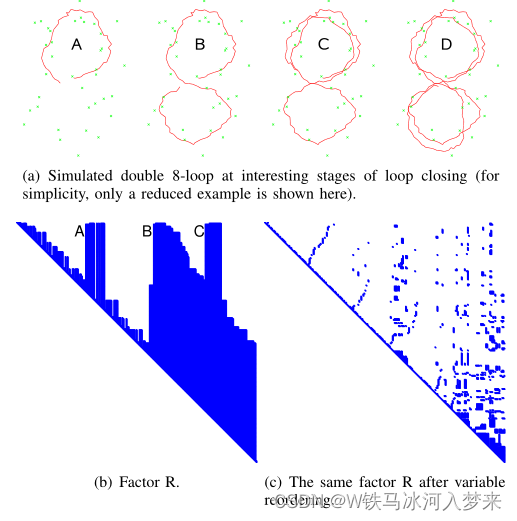
通过变量重新排序来避免矩阵$R$中大量的填充，其通过COLAMD算法来实现。COLAMD是列近似最小度排列，简单来说就是把矩阵按列重新排序，这样重新排序的好处是，重新排序的矩阵在进行矩阵分解（LU,QR等）时可以获得更稀疏的形式，从而减少计算量。如下图所示是MATLAB官方给出的一个479×479矩阵，如figure 1所示，右边A(:,p)是通过COLAMD重新排序后的形式（p是重新排序的1×479的向量）。Figure 2和Figure 3分别是矩阵A和矩阵A(:,p)进行LU分解和QR分解后的形式。可以看出重新排序后的矩阵在矩阵分解后有更稀疏的形式。

如论文中图（c）所示，重新排序后的矩阵是稀疏的。如果每100步重新排序一次，会较大地提升计算效率。

B. nonlinear Systems

由于SLAM中通常都是非线性的测量函数，在求解之后，我们通常会得到更优的估计，进而得到一个基于这个新的线性化点的修正雅可比矩阵。将其与周期性变量重排序相结合。也就是说，在变量重排序过程中也会重新线性化测量函数，因此新的测量雅可比矩阵也必须被重构。

V. DATA ASSOCIATION

SLAM中的数据关联问题包括将测量值和相应的landmarks相匹配。

A. Maximum Likelihood Data Association

采用最大似然(ML)方法来进行数据关联，因为它考虑了当前机器人位姿与地图上landmark之间的相对不确定性。它采用马氏距离：
$$\Xi =J\Sigma J^T+\Gamma$$
其中$\Gamma$是测量噪声，$J$是公式(3)中线性化后的测量函数$h$的雅可比矩阵，$\Sigma$是姿态和路标的不确定性矩阵（类似协方差）。

B. Marginal Covariances

ML方法中需要了解当前姿态$x_i$和路标$l_j$之间的相对不确定性。边际协方差：
$$\Sigma =\left[\begin{array}{cc}{\Sigma }_{jj}& {\Sigma }_{ij}^T\\ {\Sigma }_{ij}& {\Sigma }_{ii}\end{array}\right]=（A^{T}A{)}^{-1}=(R^{T}R{)}^{-1}$$

这个矩阵的计算有精确解和保守解两种计算的方法。但这两种方法的共同之处在于，都是通过平方根因子$R$来计算位姿的不确定性${\Sigma }_{ii}$以及协方差矩阵${\Sigma }_{ij}$。
当在最后添加最近的姿态时，如图所示，这种情况下只需要对角线上的一些三角形块和最后一行、一列进行更新即可，如图中灰色部分。

更新方法如下。首先令
$$B=\left[\begin{array}{c}{0}_{\left(n-d_{\mathbf{x}}\right)\times d_{\mathbf{x}}}\\ I_{d_{\mathbf{x}}\times d_{\mathbf{x}}}\end{array}\right]$$
其中$d_{\mathbf{x}}$是最后新增位姿的维度。通过求解
$$R^{T}RX=B$$
即是求解：
$$R^{T}Y=B,RX=Y$$

我们可以这么理解这个式子。令$R^{T}R=\left[\begin{array}{cc}a& b\\ b^T& d\end{array}\right]$,其中$a$是$n\times n$的，d是$d_{\mathbf{x}}\times d_{\mathbf{x}}$的。令$(R^{T}R{)}^{-1}=\left[\begin{array}{cc}e& f\\ f^T& g\end{array}\right]$,则两个矩阵相乘，可以得到：
$$\left[\begin{array}{cc}a& b\\ b^T& d\end{array}\right]\left[\begin{array}{c}f\\ g\end{array}\right]=\left[\begin{array}{c}0\\ I\end{array}\right]$$
和文中形式一致，即$X=\left[\begin{array}{c}f\\ g\end{array}\right]$。

C. Conservative Estimates

保守估计由以下公式获得：
$${\tilde{\Sigma }}_{jj}=\bar{J}\left[\begin{array}{ll}{\Sigma }_{ii}& \\ & \Gamma \end{array}\right]{\bar{J}}^T$$
其中$\bar{J}$是线性化反向投影函数的雅可比。

D. Exact Covariances

精确的结构不确定性${\Sigma }_{jj}$根据：
$$\Sigma =（A^{T}A{)}^{-1}=(R^{T}R{)}^{-1}$$
通过求解
$$R^{T}R\Sigma =I$$
即是求解：
$$R^{T}Y=I,R\Sigma =Y$$
这样的计算方式，时间复杂度是$O(n)$的。如图所示，红色是轨迹，绿色×是地标，保守协方差为绿色大椭圆，精确协方差为蓝色椭圆。其中还显示了基于完全求逆的精确协方差。可以看出该算法与精确值十分接近。

E. Evaluation

TABLE I 展示了不同方法获得边际协方差矩阵的计算时间。该结果来自于模拟环境，具有500个姿态循环和240个landmark，并且添加了测量噪声。结果显示尽管精确算法比直接求逆效率高很多，但保守解更适合实时运行。

VI. EXPERIMENTAL RESULTS AND DISCUSSION

A. Landmark-based iSAM

• 在悉尼维多利亚公园数据集上进行评估
• 4公里长的轨迹、7247帧、26min，提取了3640个landmark
• iSAM可以实时运行，基于保守估计来执行数据关联，共需要7.7min < 26min
• 在已知数据关联的情况下（实验中使用之前自动获得的对应关系），时间减少到5.9min
• 在接近轨迹终点时仍然实时运行，因为矩阵$R$仍然稀疏

B. Pose Constraint-based iSAM

• 在simulated Manhattan world数据集上评估
• 3500个姿态和5598个约束，其中3499个是里程测量
• 平均40ms/步，最后100步需要48ms
• 在其它真实数据集（Intel dataset, MIT Killian Court dataset）
  

C. Sparsity of Square Root Factor

• 如图显示了矩阵$R$的稀疏性在不同数据集上的评估
• 结果显示，除了Intel dataset，其它数据集中矩阵平均每列的元素个数都接近于收敛到常数
• 证明了假设：每列平均元素数与变量n无关
  

参考

1. Kaess, M., Ranganathan, A., & Dellaert, F. (2008). iSAM: Incremental smoothing and mapping. IEEE Transactions on Robotics, 24(6), 1365-1378.
2. [矩阵的QR分解系列二] 吉文斯(Givens)变换