iSAM1论文推导学习--第二节QR部分

iSAM1论文链接

一.基于QR分解的增量平滑优化

A.一个SLAM的概率图模型

        用下图的网络表示SLAM问题：

其中， 是机器人在时刻i的状态，是地标j的位置，是时刻i的控制输入，是第k个地标测量。

        所有变量和测量值的联合概率由以下公式表示：

其中是初始状态上的先验值，是运动学模型，由控制输入ui参数化，是地标性测量模型。这里假设每个测量值都有已知的对应关系。

        假设为高斯测量模型。则“过程模型”如下：

 该方程描述了测程传感器或扫描匹配的过程，其中是正态分布的零均值过程噪声与协方差矩阵。

        而高斯测量模型如下:

 对机器人的地标传感器进行建模，其中是正态分布的零均值测量噪声与协方差。

 B.把SLAM化为最小二乘问题

当执行平滑而不是滤波操作时，注意的是给定控制输入u和地标测量值z时，整个轨迹x和地标l的地图估计。轨迹和映射的映射估计，是通过最小化来自（1）的联合概率的负对数得到的：

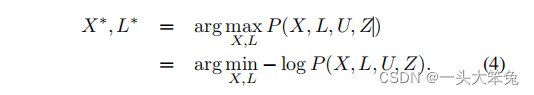
 结合过程和测量模型，则有以下非线性最小二乘问题：

 其中，这里使用符号代替平方马氏距离与协方差矩阵Σ

这里附录回顾了如何将测量函数线性化，并将非线性最小二乘目标函数（5）的所有分量收集成一个一般的最小二乘公式，遵循。通过泰勒展开式将（5）中的测量函数线性化，假设要么有一个很好的线性化点可用，或者正在进行一个非线性优化方法的一次迭代。在以上任何一种情况下，（5）中过程模型的一阶线性化给出为：

 其中，是过程模型在线性化点处的雅可比矩阵，这里定义为：

 并且，是测程预测误差(注意这里的ui是给出的，因此是常数)。而方程（5）中测量模型的一阶线性化如下：

 这里，和分别是测量函数关于在线性化点上计算的和变化的雅可比矩阵:

并且 是测量预测误差。

分别使用线性化过程和测量模型（24）和（26），则非线性最小二乘问题（5）变成：

也就是说，这里得到了δθ中一个需要有效求解的线性最小二乘问题。为了避免以一种特殊的方式处理，我们引入了矩阵,

 通过简单地改变变量，可以去掉协方差矩阵和。用作为Λ的矩阵平方根，可以将马氏范数重写如下:

 也就是说，总是可以通过将每个项中的、和预乘来从（29）中消除Λi，同样从测量项中消除。对于标量测量，这仅仅意味着将每一项除以测量的标准差。下面假设已经这样做了，然后去掉马氏符号:

最后，将雅可比矩阵收集到一个大矩阵A，将向量和收集到一个右侧向量b，得到以下标准最小二乘问题:

为了简单起见，iSAM在附录之外去掉了δ·符号,则上式变成：

 其中，向量θ∈包含所有的姿态和地标变量，矩阵A∈是一个大但稀疏的测量雅可比矩阵，b∈是右侧(RHS)向量。

通过将导数设为0，将该稀疏最小二乘系统转化为普通的线性方程组，得到所谓的正规方程。该方程系统可以用的 Cholesky 分解来求解。

 C.用QR分解法求解

将标准QR矩阵分解应用于测量雅可比矩阵A来求解最小二乘问题（6）。与Cholesky分解相比，这避免了必须用矩阵条件数的相关平方来计算信息矩阵。测量值雅可比矩阵A的QR分解得到：

 其中，R∈为上三角平方根信息矩阵(注意，信息矩阵由给出)，Q∈为正交矩阵。我们将这个因子分解应用于最小二乘问题（6）：

 其中，定义与d∈和e∈.（8）当且仅当Rθ=d时成为最小，留下第二项作为最小二乘问题的残差。因此，QR分解将最小二乘问题简化为具有单一唯一解的线性系统：

 求解这个方程组的大部分工作已经通过QR分解完成了，因为R是上三角的，所以可以使用简单的反替换。结果是基于所有测量条件的完整机器人轨迹和地图的最小二乘估计。