iSAM
主要参考论文
论文名iSAM: Incremental Smoothing and Mapping
作者Michael Kaess, Student Member, IEEE, Ananth Ranganathan, Student Member, IEEE,and Frank Dellaert, Member, IEEE
期刊: 2008 T-RO
因子图
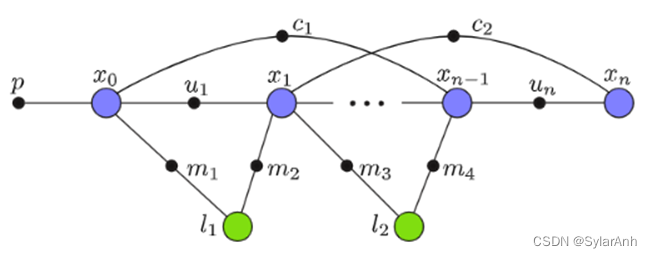
因子图也是一种图结构,由顶点和边组成,顶点就是我们的待优化的变量,或者参数,对应批量优化就是机器人的状态变量和环境中需要定位的landmark参数。这里的边描述为连接两个参数的因子,物理意义为当前两种参数状态下的观测,可以是连接两个机器人状态量的里程计信息(雷达视觉imu里程计等),也可以指机器人状态到环境变量的观测。
问题转化
因子图的优化目标是图中所有状态参数变量,使得所有观测因子的连乘结果最大,每个因子认为服从高斯分布。问题描述如下:
f i ( Θ i ) ∝ exp ( − 1 2 ∥ h i ( Θ i ) − z i ∥ Σ i 2 ) f ( Θ ) = ∏ i f i ( Θ i ) Θ ∗ = arg max Θ f ( Θ ) f_{i}\left(\Theta_{i}\right) \propto \exp \left(-\frac{1}{2}\left\|h_{i}\left(\Theta_{i}\right)-z_{i}\right\|_{\Sigma_{i}}^{2}\right)\\ f(\Theta)=\prod_{i} f_{i}\left(\Theta_{i}\right)\\ \Theta^{*}=\underset{\Theta}{\arg \max } f(\Theta) fi(Θi)∝exp(−21∥hi(Θi)−zi∥Σi2)f(Θ)=i∏fi(Θi)Θ∗=Θargmaxf(Θ)
将问题的目标函数在初始的参数位置进行线性化得到如下表达式:
arg min Δ ( − log f ( Δ ) ) = arg min Δ ∥ A Δ − b ∥ 2 \underset{\Delta}{\arg \min }(-\log f(\Delta))=\underset{\Delta}{\arg \min }\|A \Delta-\mathbf{b}\|^{2} Δargmin(−logf(Δ))=Δargmin∥AΔ−b∥2
这样就将非线性最小二乘问题转化成了线性最小二乘问题,注意到其中的:
A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n
m为测量行 n为变量数,对于因子图问题每多一个新的状态量一定会多至少一个因子,因此m总是大于n的。A是长条形的,因此对A进行QR分解得到:
A = Q [ R 0 ] A=Q\left[\begin{array}{l} R \\ 0 \end{array}\right] A=Q[R0]
最小二乘问题化简成:
∥ A θ − b ∥ 2 = ∥ Q [ R 0 ] θ − b ∥ 2 = ∥ Q T Q [ R 0 ] θ − Q T b ∥ 2 = ∥ [ R 0 ] θ − [ d e ] ∥ 2 = ∥ R θ − d ∥ 2 + ∥ e ∥ 2 \begin{aligned} \|A \boldsymbol{\theta}-\mathbf{b}\|^{2} &=\left\|Q\left[\begin{array}{c} R \\ 0 \end{array}\right] \boldsymbol{\theta}-\mathbf{b}\right\|^{2} \\ &=\left\|Q^{T} Q\left[\begin{array}{c} R \\ 0 \end{array}\right] \boldsymbol{\theta}-Q^{T} \mathbf{b}\right\|^{2} \\ &=\left\|\left[\begin{array}{c} R \\ 0 \end{array}\right] \boldsymbol{\theta}-\left[\begin{array}{l} \mathbf{d} \\ \mathbf{e} \end{array}\right]\right\|^{2} \\ &=\|R \boldsymbol{\theta}-\mathbf{d}\|^{2}+\|\mathbf{e}\|^{2} \end{aligned} ∥Aθ−b∥2=∥ ∥Q[R0]θ−b∥ ∥2=∥ ∥QTQ[R0]θ−QTb∥ ∥2=∥ ∥[R0]θ−[de]∥ ∥2=∥Rθ−d∥2+∥e∥2
后半部分为常数部分,前半部分为二次型,最小值为零,因此最小二乘问题被转换成上式前半部分的线性方程组的解。
增量式因子图构建与问题求解
如上理论推导是为非线性最小二乘的共性问题,iSAM主要提出了增量更新方法:
[ Q T 1 ] [ A w T ] = [ R w T ] , new rhs: [ d γ ] \left[\begin{array}{ll} Q^{T} & \\ & 1 \end{array}\right]\left[\begin{array}{c} A \\ \mathbf{w}^{T} \end{array}\right]=\left[\begin{array}{c} R \\ \mathbf{w}^{T} \end{array}\right] \text {, new rhs: }\left[\begin{array}{c} \mathbf{d} \\ \gamma \end{array}\right] [QT1][AwT]=[RwT], new rhs: [dγ]
当获得了新的测量行时雅克比矩阵A下方多了一行新测量因子线性化项(行),该线性化项(行)列数可以比A多,用0补齐A右侧即可,且是稀疏的,因为仅有特定的参数状态(列)与该因子有关,当新的增量雅克比矩阵左乘原正交矩阵时(相差的行列用单位矩阵补齐,此时仍是正交的)就可以得到R矩阵的增量表达,增量方式与A相同,注意此时新增的行依然是稀疏的。
时只需要对R矩阵进行Givens旋转变换就可以将下面的非零项消除,得到新的R矩阵:
[ R ′ 0 ] \left[\begin{array}{c} R^{\prime} \\ 0 \end{array}\right] [R′0]
这样就完成了一次增量更新,我们注意到使用iSAM在这种情况下可以只对新增的测量因子线性化,也不需要对雅可比矩阵A重新QR分解,就得到了我们想要的结果,这一过程像滤波算法一样简单,但却可以得到批量优化一样好的全局最优效果。这就是iSAM的闪光点。
是不是能一直这样方便下去呢?答案实际是不行的,我们得到如此好的结果是基于R矩阵是稀疏的前提条件。Givens旋转是在n维空间中旋定两组正交基张成的空间中旋转。
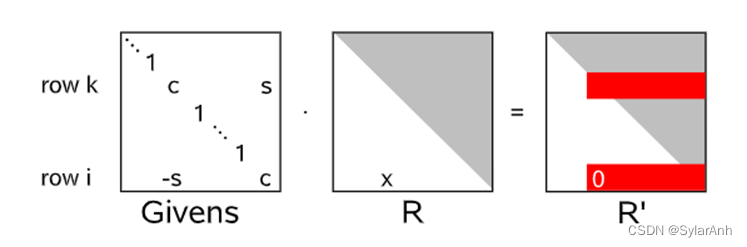
也就是说在消去R底部对应行的过程中,上面的某一行也在发生着改变,稀疏性会逐渐的遭到破坏如下图所示:
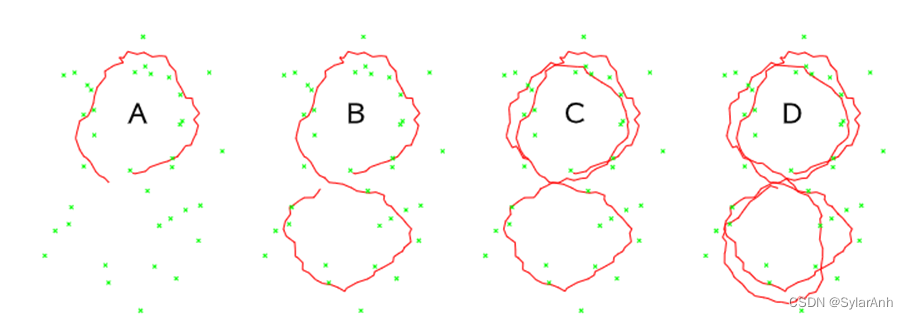

因此需要周期性的重排序,来恢复矩阵的稀疏性。这一过程则极为耗时。
因此iSAM抛出问题:如何减少重排序的次数,如何降低新增状态量,对R矩阵稀疏性的破坏程度。
iSAM2
主要参考论文
论文名iSAM2: Incremental smoothing and mapping using the Bayes tree
作者Michael Kaess, Hordur Johannsson, Richard Roberts, Viorela Ila, John Leonard, and Frank Dellaert
期刊: 2012 IJRR
一些铺垫
这篇文章的核心在于引入了贝叶斯树,从而解决了减少了或者优化了,iSAM1中遗留下来的问题。那么什么是贝叶斯树呢?
定义一下文章中说到的术语:
消元/消去:代表由因子图转换为贝叶斯网络的过程中一步操作,将因子图中的一个节点和相连的因子边转换为贝叶斯网络中的节点和有向边的过程。
首先我认为贝叶斯树本身并没有特别的意义,真正的价值在于你维护树的过程,当你按照贝叶斯树的法则去维护这些变量和状态的关系时,你会惊讶的发现你每次求解问题的规模都是小的,求解的矩阵都是稀疏的,最终你的问题过程都是容易解决的。就像求解方程组,再好的算法都很难从时间复杂度上简化求解方程组。但是好的算法你会发现每一步求解都是十分easy的。或者像堆排序算法,关键在于你维护这个堆的过程。
因子图定义和前面的文章一样并没有变化。但是贝叶斯树是基于贝叶斯网络演变过来的,贝叶斯网络可以参考贝叶斯网专题2:贝叶斯网基本概念_吴智深的博客-CSDN博客.这里面有很细致的介绍。
许多概率问题直接使用联合分布进行不确定性推理的复杂度很高。因此,联合分布的复杂度与变量个数呈指数增长。当变量很多时,联合概率的获取、存储和运算都变得十分困难。
如果通过连规则将联合概率分布分解为条件概率乘积的形式,再根据变量之间的独立性进行化简,问题就会简化很多。最后将变量之间的依赖关系用有向箭头表示就得到了贝叶斯网。
P
(
B
,
E
,
A
,
J
,
M
)
=
P
(
B
)
P
(
E
∣
B
)
P
(
A
∣
B
,
E
)
P
(
J
∣
B
,
E
,
A
)
P
(
M
∣
B
,
E
,
A
,
J
)
P
(
B
,
E
,
A
,
J
,
M
)
=
P
(
B
)
P
(
E
)
P
(
A
∣
B
,
E
)
P
(
J
∣
A
)
P
(
M
∣
A
)
\begin{aligned} & P(B, E, A, J, M) \\ =& P(B) P(E \mid B) P(A \mid B, E) P(J \mid B, E, A) P(M \mid B, E, A, J) \end{aligned}\\P(B, E, A, J, M)=P(B) P(E) P(A \mid B, E) P(J \mid A) P(M \mid A)
=P(B,E,A,J,M)P(B)P(E∣B)P(A∣B,E)P(J∣B,E,A)P(M∣B,E,A,J)P(B,E,A,J,M)=P(B)P(E)P(A∣B,E)P(J∣A)P(M∣A)

首先求解因子图模型可以理解为概率推理的过程,每个因子本身可以看作是在当前观测条件下,关联的变量联合概率分布。因此用贝叶斯网络进行替换也是高效的。
因子图可以转换成贝叶斯网络。因子图问题中其实没有因果关系,但是依然可以表达成条件概率乘以边缘概率的形式,形如下式。
f
joint
(
θ
j
,
S
j
)
=
P
(
θ
j
∣
S
j
)
f
new
(
S
j
)
f_{\text {joint }}\left(\theta_{j}, S_{j}\right)=P\left(\theta_{j} \mid S_{j}\right) f_{\text {new }}\left(S_{j}\right)
fjoint (θj,Sj)=P(θj∣Sj)fnew (Sj)
边缘概率可能描述的不准确,因为分解只是对部分因子进行操作,并不代表已经包含了所有关于边缘某变量的因子,因此、分解得到的条件变量的因子
f
new
(
S
j
)
f_{\text {new }}\left(S_{j}\right)
fnew (Sj)并不等于最终该变量的边缘概率分布。所以这个
f
new
(
S
j
)
f_{\text {new }}\left(S_{j}\right)
fnew (Sj)暂时并不具备实际意义,只是一个形如高斯分布的函数而已。
但是前面的
P
(
θ
j
∣
S
j
)
P\left(\theta_{j} \mid S_{j}\right)
P(θj∣Sj)却是实实在在的前向变量的条件概率密度,为什么呢?
这就需要介绍一下分解的过程了,也就是从因子图生成贝叶斯网络的过程。
这个是因子图

变量还是那些变量,边变成了有向边,边的顺序与变量的消元顺序息息相关。我们先从图的角度描述消元过程介绍是怎么由第一张图变到第二张图的。下图是论文中给出的完整消元过程,作者给出的消元顺序为
l
1
l
2
x
1
x
2
x
3
l_{1}l_{2}x_{1}x_{2}x_{3}
l1l2x1x2x3
 以
l
1
l_{1}
l1为例首先将和变量
l
1
l_{1}
l1相连的所有因子边断开,替换成指向
l
1
l_{1}
l1的有向边,然后所有与变量
l
1
l_{1}
l1相连的状态或变量之间两两添加一条因子边,如果只有单个变量则添加一个因子(消除
l
2
l_{2}
l2时
x
3
x_{3}
x3添加的红色点线),这些因子可以和原有的因子结合起来(连乘)。这样逐个消去就是图视角的变换。
以
l
1
l_{1}
l1为例首先将和变量
l
1
l_{1}
l1相连的所有因子边断开,替换成指向
l
1
l_{1}
l1的有向边,然后所有与变量
l
1
l_{1}
l1相连的状态或变量之间两两添加一条因子边,如果只有单个变量则添加一个因子(消除
l
2
l_{2}
l2时
x
3
x_{3}
x3添加的红色点线),这些因子可以和原有的因子结合起来(连乘)。这样逐个消去就是图视角的变换。
这个过程和QR分解是一致的,我们先从外观上对比一下。
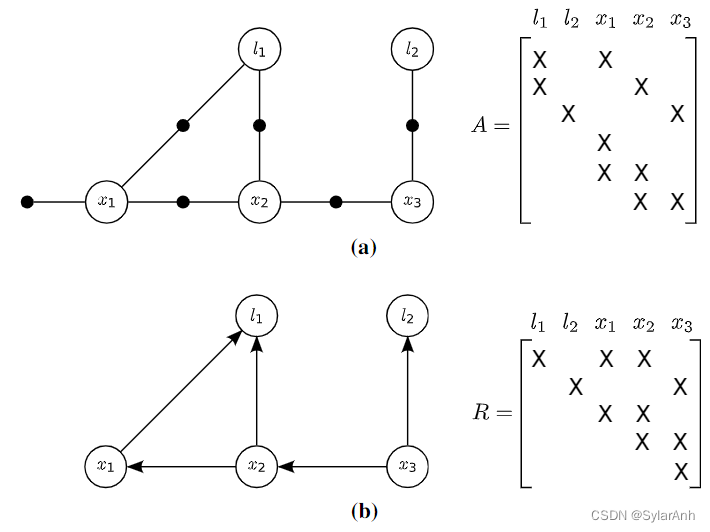
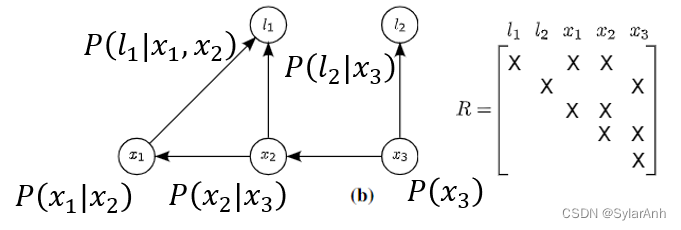
(a)A为因子模型的雅可比矩阵,行为测量因子,列为状态变量,每个因子只和部分状态向量是相关联的,因此A矩阵也是稀疏的。关联性自然和图模型是一致对应的。
(b)R矩阵为A矩阵QR分解或者Cholesky分解得到的上三角矩阵,对角元素为该行所条件概率密度
P
(
θ
j
∣
S
j
)
P\left(\theta_{j} \mid S_{j}\right)
P(θj∣Sj)对应的状态变量前向变量,同行剩下的元素对应条件概率密度中的条件变量。也可以看出二者是一致对应的。类比一下求解方程组时,从下往上依次回代求解的过程,与联合概率密度函数链分解后求最大分布的过程是一样的,我们也是先从边缘概率求极值然后将得到的取值作为条件回代到下一个,以该变量为条件的条件概率密度中,然后再求极值。举个例子:
P
(
B
,
E
,
A
,
J
,
M
)
=
P
(
B
)
P
(
E
)
P
(
A
∣
B
,
E
)
P
(
J
∣
A
)
P
(
M
∣
A
)
P(B, E, A, J, M)=P(B) P(E) P(A \mid B, E) P(J \mid A) P(M \mid A)
P(B,E,A,J,M)=P(B)P(E)P(A∣B,E)P(J∣A)P(M∣A)
式中BE事件是独立的且已知分布,因此可以直接对BE密度函数求极值,线性化之后就是很简单的二次型很好求解。在已知BE分布之后A的条件概率密度就确定了,也是一个简单的二次型。如此递推。这和求方程组的变量回代过程是一样的。
思考一下为什么一样,这就要看文中所提出来的因子分解方法。也就是说消元的过程中实际上对因子函数做了什么。
待分解因子 f joint ( Δ j , s j ) ∝ exp { − 1 2 ∥ a Δ j + A S s j − b ∥ 2 } f_{\text {joint }}\left(\Delta_{j}, \mathbf{s}_{j}\right) \propto \exp \left\{-\frac{1}{2}\left\|\mathbf{a} \Delta_{j}+\mathbf{A}_{S} \mathbf{s}_{j}-\mathbf{b}\right\|^{2}\right\} fjoint (Δj,sj)∝exp{−21∥aΔj+ASsj−b∥2}为与待消除变量相连的全部因子的连乘获得的,前面已经介绍过。
先给出结论分解出的条件概率,边缘因子解析表达式如下:
f
joint
(
θ
j
,
S
j
)
=
P
(
θ
j
∣
S
j
)
f
new
(
S
j
)
P
(
Δ
j
∣
s
j
)
∝
exp
{
−
1
2
(
Δ
j
+
r
s
j
−
d
)
2
}
f
n
e
w
(
s
j
)
=
exp
{
−
1
2
∥
A
′
s
j
−
b
′
∥
2
}
f_{\text {joint }}\left(\theta_{j}, S_{j}\right)=P\left(\theta_{j} \mid S_{j}\right) f_{\text {new }}\left(S_{j}\right)\\ P\left(\Delta_{j} \mid \mathbf{s}_{j}\right) \propto \exp \left\{-\frac{1}{2}\left(\Delta_{j}+\mathbf{r s}_{j}-d\right)^{2}\right\}\\ f_{n e w}\left(\mathbf{s}_{j}\right)=\exp \left\{-\frac{1}{2}\left\|\mathbf{A}^{\prime} \mathbf{s}_{j}-\mathbf{b}^{\prime}\right\|^{2}\right\}
fjoint (θj,Sj)=P(θj∣Sj)fnew (Sj)P(Δj∣sj)∝exp{−21(Δj+rsj−d)2}fnew(sj)=exp{−21∥A′sj−b′∥2}
其中
r
≜
a
†
A
S
,
d
≜
a
†
b
,
a
†
≜
(
a
T
a
)
−
1
a
T
\mathbf{r} \triangleq \mathbf{a}^{\dagger} \mathbf{A}_{S}, d \triangleq \mathbf{a}^{\dagger} \mathbf{b}, \mathbf{a}^{\dagger} \triangleq\left(\mathbf{a}^{T} \mathbf{a}\right)^{-1} \mathbf{a}^{T}
r≜a†AS,d≜a†b,a†≜(aTa)−1aT
其中第二项是通过将第一项得到的变量增量的最优解析表达
Δ
j
=
d
−
r
s
j
\Delta_{j}=d-\mathbf{r s}_{j}
Δj=d−rsj回代回因子中得到的余项。也就是要传递给贝叶斯网络中父节点的边缘因子。(对应图视角下的相连的状态或变量之间两两添加一条因子边的过程。)
原文中只是给出了解析表达并没有附上详细的证明,笔者尝试证明了一下:
待求最小值的二次型为
∥
a
Δ
j
+
A
S
s
j
−
b
∥
2
\left\|\mathbf{a} \Delta_{j}+\mathbf{A}_{S} \mathbf{s}_{j}-\mathbf{b}\right\|^{2}
∥aΔj+ASsj−b∥2
=
∥
[
a
∣
a
∣
a
1
…
a
m
j
−
1
]
[
∣
a
∣
0
]
Δ
j
+
A
s
s
j
−
b
∥
2
=\left\|\left[\frac{\boldsymbol{a}}{|\boldsymbol{a}|} \quad \boldsymbol{a}_{1} \quad \ldots \quad \boldsymbol{a}_{m_{j}-1}\right]\left[\begin{array}{c} |\boldsymbol{a}| \\ 0 \end{array}\right] \Delta_{j}+A_{s} \boldsymbol{s}_{j}-\boldsymbol{b}\right\|^{2}
=∥
∥[∣a∣aa1…amj−1][∣a∣0]Δj+Assj−b∥
∥2
其中 a m j − 1 \boldsymbol{a}_{m_{j}-1} amj−1为补全的单位正交基
上式左乘一个单位正交矩阵不影响其二范数取值,那么就左乘刚刚提取出来的正交矩阵的转置。
=
∥
[
∣
a
∣
0
]
Δ
j
+
[
a
T
∣
a
∣
a
1
T
⋮
a
m
j
−
1
T
]
A
S
s
j
−
[
a
T
∣
a
∣
a
1
T
⋮
a
m
j
−
1
T
]
∥
∥
2
=
∥
∣
a
∣
Δ
j
+
a
T
∣
a
∣
A
S
s
j
−
a
T
∣
a
∣
b
∥
2
+
∥
[
a
1
T
A
s
s
j
⋮
a
m
j
−
1
T
A
s
s
j
]
−
[
a
1
T
b
⋮
a
m
j
−
1
T
b
]
∥
2
=\left\|\left[\begin{array}{c} |\boldsymbol{a}| \\ 0 \end{array}\right] \Delta_{j}+\left[\begin{array}{c} \frac{\boldsymbol{a}^{T}}{|\boldsymbol{a}|} \\ \boldsymbol{a}_{1}^{T} \\ \vdots \\ \boldsymbol{a}_{m_{j}-1}^{T} \end{array}\right] A_{S} s_{j}-\left[\begin{array}{c} \frac{\boldsymbol{a}^{T}}{|\boldsymbol{a}|} \\ \boldsymbol{a}_{1}^{T} \\ \vdots \\ \boldsymbol{a}_{m_{j}-1}^{T} \end{array}\right]\right\| \|^{2}\\ =\left\||\boldsymbol{a}| \Delta_{j}+\frac{\boldsymbol{a}^{\boldsymbol{T}}}{|\boldsymbol{a}|} A_{S} s_{j}-\frac{\boldsymbol{a}^{\boldsymbol{T}}}{|\boldsymbol{a}|} \boldsymbol{b}\right\|^{2}+\left\|\left[\begin{array}{c} \boldsymbol{a}_{1}{ }^{T} A_{s} \boldsymbol{s}_{j} \\ \vdots \\ \boldsymbol{a}_{m_{j}-1}{ }^{T} A_{s} \boldsymbol{s}_{j} \end{array}\right]-\left[\begin{array}{c} \boldsymbol{a}_{1}{ }^{T} \boldsymbol{b} \\ \vdots \\ \boldsymbol{a}_{m_{j}-1}{ }^{T} \boldsymbol{b} \end{array}\right]\right\|^{2}
=∥
∥[∣a∣0]Δj+⎣
⎡∣a∣aTa1T⋮amj−1T⎦
⎤ASsj−⎣
⎡∣a∣aTa1T⋮amj−1T⎦
⎤∥
∥∥2=∥
∥∣a∣Δj+∣a∣aTASsj−∣a∣aTb∥
∥2+∥
∥⎣
⎡a1TAssj⋮amj−1TAssj⎦
⎤−⎣
⎡a1Tb⋮amj−1Tb⎦
⎤∥
∥2
左边是与当前待求参数相关的数值平方项,右面是与当前待求参数无关的二范数项,分别对应条件概率密度(未归一化)和边缘因子。与作者所描述分解方法相符。
从上述推导可以看出,由因子图转换成贝叶斯网络的过程中,每一步实际在做的是一步QR分解,宏观上消元顺序对应QR分解顺序。
到此就基本解释了图视角和矩阵变换视角的对应关系,以及其对应的概率分解运算步骤。
贝叶斯树
首先建议先看一下团树,因为作者反复提到贝叶斯树是与团树或者联结树由很高的相似性并且从中发展来的。贝叶斯网专题6:团树传播_吴智深的博客-CSDN博客_团树传播算法.
团树与贝叶斯树一样,将变量集合存成节点,集合之间可以有重复变量,两个包含相同变量的节点之间一定是连通的。不同的是贝叶斯树是有向的。
团树的优势之一在于推理的复用,举个例子一个概率模型中包含甲乙丙丁四个变量,我推理完甲的条件概率,当我需要推理乙的条件概率时,可以复用甲推理过程中的部分中间推理结果。使用团树可以很清晰的维护这些中间结果,方便信息传递以及推理复用。
当我们求解因子图问题时,新增的变量和测量难免会改变模型结构,但是并不一定会直接影响全局的贝叶斯网络结构,还用论文中的例子:当
x
2
,
x
3
x_{2}, x_{3}
x2,x3之间添加了新的测量,其实并不影响
l
2
l_{2}
l2的消元过程,也不改变
l
2
l_{2}
l2向
x
3
x_{3}
x3传递的边缘因子。因此贝叶斯树也被用来存储一定的复用关系,当子树中变量未受影响时,子树结构和推理结果(从子树中传递上来的边缘因子)都不发生改变。贝叶斯树的生成方式伪代码附在下面。

总结来说,就是逆着消元的过程检索生成贝叶斯树。如果某贝叶斯网络中的节点(变量)完全以其父团为条件变量,那就加入父团,如果不“完全”就新建一个子团,父子团之间使用有向边连接。个人理解贝叶斯树代表着QR矩阵中的最小稠密单元。还是看文中提到的例子,按照作者的方法生成的贝叶斯树如左图所示,对应变量在矩阵中的关系如右图所示。R矩阵是稀疏的,将R矩阵拆成一个个稠密的最小单元得到的就是贝叶斯树。每个树节点(变量团)都是完全稠密的。其中冒号表示分隔关系,冒号前为前向变量,冒号后为条件变量,文中叫分隔变量。
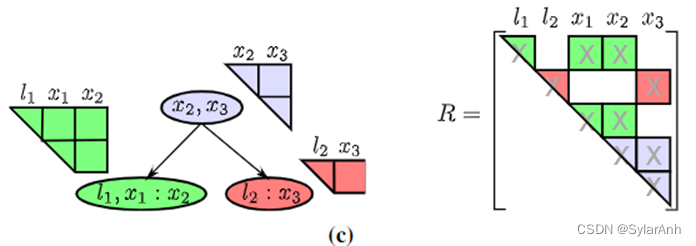
当新增测量因子时,比如当
x
2
,
x
3
x_{2}, x_{3}
x2,x3之间产生了共视关系。那么含有
x
2
x_{2}
x2的团
l
1
,
x
1
:
x
2
l_{1}, x_{1}: x_{2}
l1,x1:x2
及其父团都将受到影响,如图所示圈中的团受到影响。而绿色的子树部分没有受到影响。
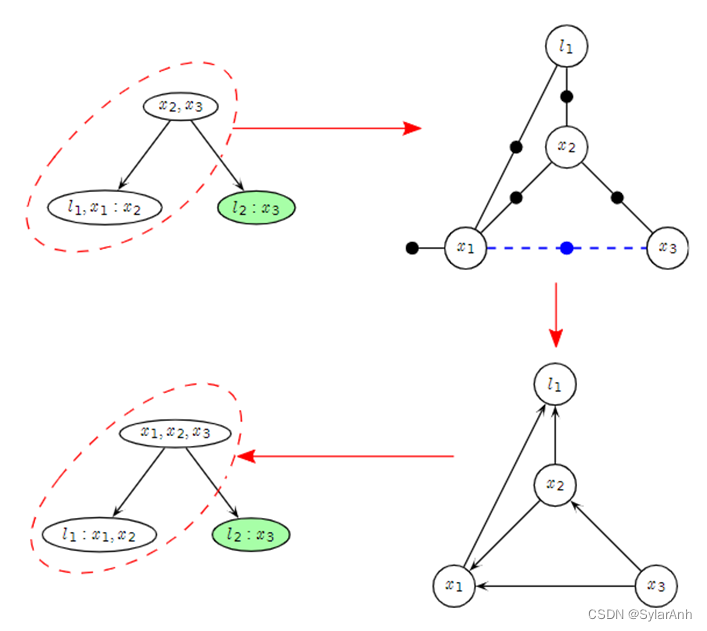
增量更新时,将受影响的树顶部分删除,并重建因子图,然后选择最优的消元顺序重新生成贝叶斯树,然后将子树连接回来。
这里说明了贝叶斯树是更好的维持了与线性代数的等价性,并使算法支持递归估计,可并行计算。
整个逻辑推理其实可以大致分为两个过程,第一步是从贝叶斯网络叶子节点向其根部的因子分解过程,这一步对应因子图生成贝叶斯网的消元过程,每次都将与当前节点(变量)无关的分离出来的边缘因子传递给其父节点,称之为由下到上的过程;第二步是从父节点开始依次计算出当前节点的最优增量值大小,其已经由第一步消元过程中计算出了解析表达 Δ j = d − r s j \Delta_{j}=d-\mathbf{r s}_{j} Δj=d−rsj只需要回代即可,称之为由上到下的过程。
我们注意到当变量的增量值已经很大时,是需要重线性化的,文中使用阈值来判断哪些变量需要重线性化。同时使用另一个阈值来判断,重新线性化后或者添加了新的变量或者测量之后,第二步,从上到下计算增量,的过程是否需要重新计算(因为条件变量的取值变了,但是如果增量变化很小的话,就可以停止这个计算过程。下面的子树中的增量就也不需要更新了)。这两步属于加速算法的trick,利用的是,slam问题新的观测往往对较远的状态估计产生很小的影响。
此外就是每次贝叶斯树的生成过程中,消元顺序的选择,这里会最终影响贝叶斯树的结构。求最优消元顺序实际上是NP难的问题,一般使用启发式的方法求解。
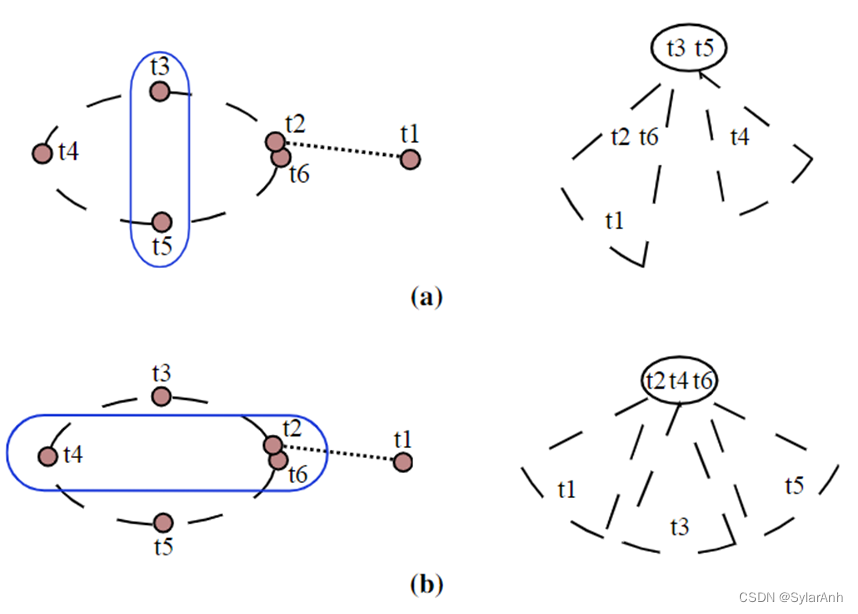
文中介绍了一种启发性,当消去顺序将导致新的观测聚集在树根部分时是比较好的,因为新的测量添加进来时,对数结构破坏程度最小。
总结
总结一下贝叶斯树是如何处理iSAM1遗留下来的问题:
如何减少重排序的次数,如何降低新增状态量,对R矩阵稀疏性的破坏程度
- 变量消除法实际上是在对雅可比矩阵求QR分解,只不过不需要全局分解,可以通过逐步的局部操作完成,这样就说明了局部的QR分解不会影响全局的一致性。是后面贝叶斯树可以局部更新的前提。
- 贝叶斯树,通过维护树结构,当新增状态量时,通过树结构快速找出,受影响的其他变量,将该部分树结构删除,并重新线性化生成贝叶斯网再生成贝叶斯树。而其他未受影响的子树结构得以保留,从而减少了计算。
- 同时在重新生成贝叶斯网的过程中,局部的变量顺序得到重新排序,从而使未来添加新变量的代价最小(贝叶斯树改动,以及需要分解的因子图规模最小)。举个例子,如果把iSAM1需要周期性的批处理来得到较优的变量消元顺序,比作打扑克时,抽完所有牌再理牌的话,那么贝叶斯树的增量更新过程更像是再每次抓牌的过程中都将局部牌序调整到一个比较优的顺序,从而长期保持矩阵的稀疏性。但是是否能一直保持下去呢,答案是不能的,当遇到意料外的大回环,还是会影响很大一部分的树结构,从而导致大规模的因子图重建,排序消元,构建贝叶斯树。因此减少但并没有完全解决这个问题。
























 5036
5036











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








