计算机视觉中的数学方法——1平面射影几何——1射影平面+2二次曲线

小白想入门计算机视觉领域，看过了数字图像处理，找到了这本《计算机视觉中的数学方法》，看了下内容适中，结构和multiple view geometry基本一致，有些内容更为细致，但对我只有考研基础的人来说还是有些难度，且行且珍惜，努力吧。2019.9.12

1．平面射影几何

1.1 射影平面

1.1.1 射影平面

1.1.2 两点、两线的叉积

三维向量的叉积

注：
性质2：将向量叉乘转化为矩阵与向量相乘，简化计算。
性质4：
两点、两线的叉积


反对称阵转置等于其加负号

1.1.3 共线点、共点线的交比

是建立直线坐标系的过程。直线上点的参数化不是唯一的，不同的参数化对应不同的坐标系。

感觉推导的上标有点问题：

（矩阵A、B存在以下等式： |AB|=|A||B|）


这是常用的交比计算公式。
若( p1, p2 ; p3 , p4 ) = −1，则称 p1, p2与p3, p4成调和共轭。
（例如，通过圆心的直线交圆上的两个点与圆心以及该直线上的无穷远点成调和共轭。 ）

注：P1-P2=该直线无穷远点，l=(a,b,c) ,无穷远点=(-b,a,0)


相当于共线点的对偶

红圈部分应该乘个-1？？？，结论是对的。

1.2 二次曲线

1.2.1 矩阵表示

注意和叉乘矩阵的不同，一个是对角线为0的反对称阵。


任两直线按如上构建方式会生成一个奇异对称阵

1.2.2 切线

反证法证明直接将(sp + tq)T C(sp + tq) = 0展开即可得到对任何标量s、t成立。与p、q共线l上的点r满足r=sp+tq，所以得到结论l与C应是重合。

退化的二次曲线就是直线，过某点切线就是其退化二次曲线自身。
这里mTp运算完为一个标量，所以提到了前面，齐次坐标下l与Cp只差一个标量mTp所以为同一条直线。

tips 两点p叉乘q确定一条直线l过这两点。

1.2.3 配极对应（变换）

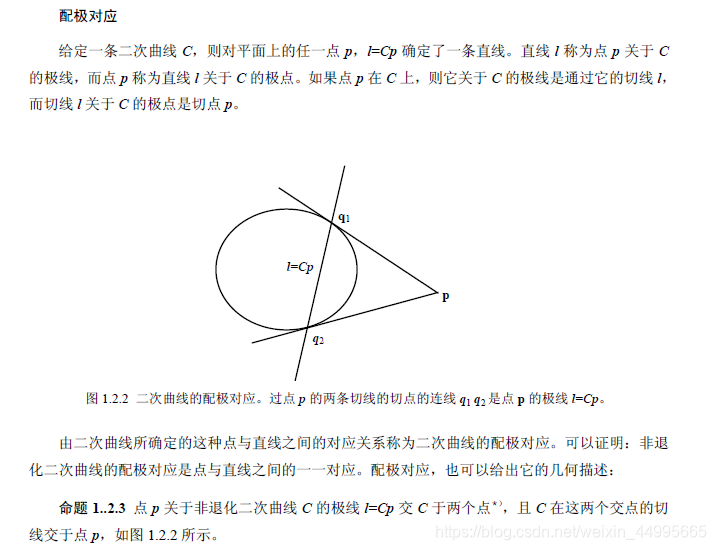
l^Tq = (Cp)^Tq=0

1. p^TCq = 0=(Cp)^Tq=l^Tq=0,l为极线。
2. 
3. p^TCp运算结果为标量
   

1.2.4 对偶二次曲线

退化的对偶二次曲线有啥用呢？

1.2.5 圆环点及其对偶

标必为I，J。现在，也可以解释为什么给定三个点能唯一确定一个圆，因为圆总是通过两个圆环点。所以，3 点确定一个圆与5 个点才能确定一条二次曲线并不矛盾。

1. 过平面内任意一点至两圆环点的两条直线，称为该点的迷向直线(极小直线)。
2. 平面上，一条直线以及平行于这条直线的全体直线的集合叫做平行直线束。
3. 迷向直线不象通常直线那样具有方向。
   
   此处证明只需要将l1及l2的齐次表示带入即可得到文中三个证明式子。
   
4. 设直线L1斜率为K1，直线L2斜率为K2，两条直线的夹角α，tanα=(K1-K2)/(1+K1*K2)
5. 
6. 
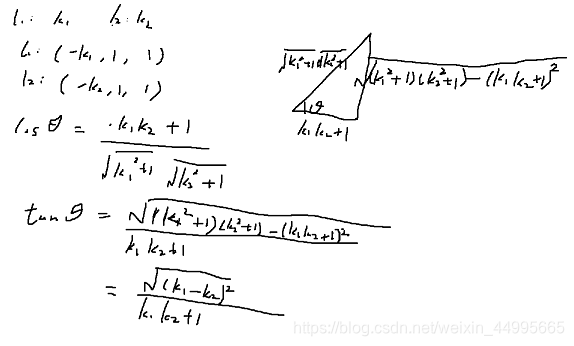
7. 调和共轭，交比为-1；
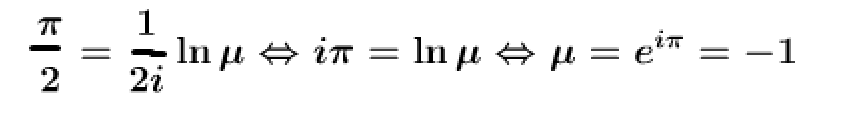
   花了一天半时间看到了这里，主要是之前看过Multiple view geometry的前几章所以这一块看起来没有那么费劲。再难的知识只要过几天多看几遍，一定会有新体会的，加油。2019.9.13