问题引入
在2维平面直角坐标系下,逆时针旋转的公式为:
x
′
=
x
c
o
s
α
−
y
s
i
n
α
y
′
=
x
s
i
n
α
+
y
c
o
s
α
x' = xcos\alpha - ysin\alpha\\ y' = xsin\alpha + ycos\alpha
x′=xcosα−ysinαy′=xsinα+ycosα
用矩阵表示为:
[
x
′
y
′
]
=
[
c
o
s
α
−
s
i
n
α
s
i
n
α
c
o
s
α
]
×
[
x
y
]
=
R
×
[
x
y
]
\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = R \times \begin{bmatrix} x \\ y \end{bmatrix}
[x′y′]=[cosαsinα−sinαcosα]×[xy]=R×[xy]
在右手坐标系中,用齐次坐标表示为:
[
x
′
y
′
z
′
1
]
=
[
c
o
s
α
−
s
i
n
α
0
0
s
i
n
α
c
o
s
α
0
0
0
0
1
0
0
0
0
1
]
×
[
x
y
z
1
]
=
R
z
(
α
)
×
[
x
y
z
1
]
\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} cos\alpha & -sin\alpha & 0 & 0 \\ sin\alpha & cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = R_z(\alpha)\times \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}
x′y′z′1
=
cosαsinα00−sinαcosα0000100001
×
xyz1
=Rz(α)×
xyz1
而 R x ( α ) R_x(\alpha) Rx(α)和 R y ( α ) R_y(\alpha) Ry(α)分别为 [ 1 0 0 0 0 c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 ] 、 [ c o s α 0 s i n α 0 0 1 0 0 − s i n α 0 c o s α 0 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}、\begin{bmatrix} cos\alpha & 0 & sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -sin\alpha & 0 & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} 10000cosαsinα00−sinαcosα00001 、 cosα0−sinα00100sinα0cosα00001 ,可以看到只有 R y ( α ) R_y(\alpha) Ry(α)有些"另类",这是肾么回事呢?
思考
问题的关键在于坐标轴的相互顺序,我们用叉乘描述前者。
"正常的" R y ( α ) R_y(\alpha) Ry(α)(即与 R z ( α ) R_z(\alpha) Rz(α)和 R x ( α ) R_x(\alpha) Rx(α)相同)会在如下的坐标系下成立:从 y y y 轴逆向看去, x x x 为横轴, z z z 为纵轴,即 x x x- z z z 坐标系,用叉乘描述为 x × z → y x \times z \rightarrow y x×z→y。(为何就是在这样的坐标系下成立?暂且按下不表)
而右手坐标系具有循环对称性质:
x
×
y
→
z
、
y
×
z
→
x
、
z
×
x
→
y
x \times y \rightarrow z、y \times z \rightarrow x、z \times x \rightarrow y
x×y→z、y×z→x、z×x→y。而从
y
y
y 轴逆向看去,
x
x
x 是纵轴,
z
z
z 是横轴,即
z
z
z-
x
x
x 坐标系,与上面正好相反。在
x
x
x-
z
z
z 下逆时针旋转在
z
z
z-
x
x
x 下会变为顺时针。故矩阵有所变化,四个三角函数值形成的矩阵为原来的逆。
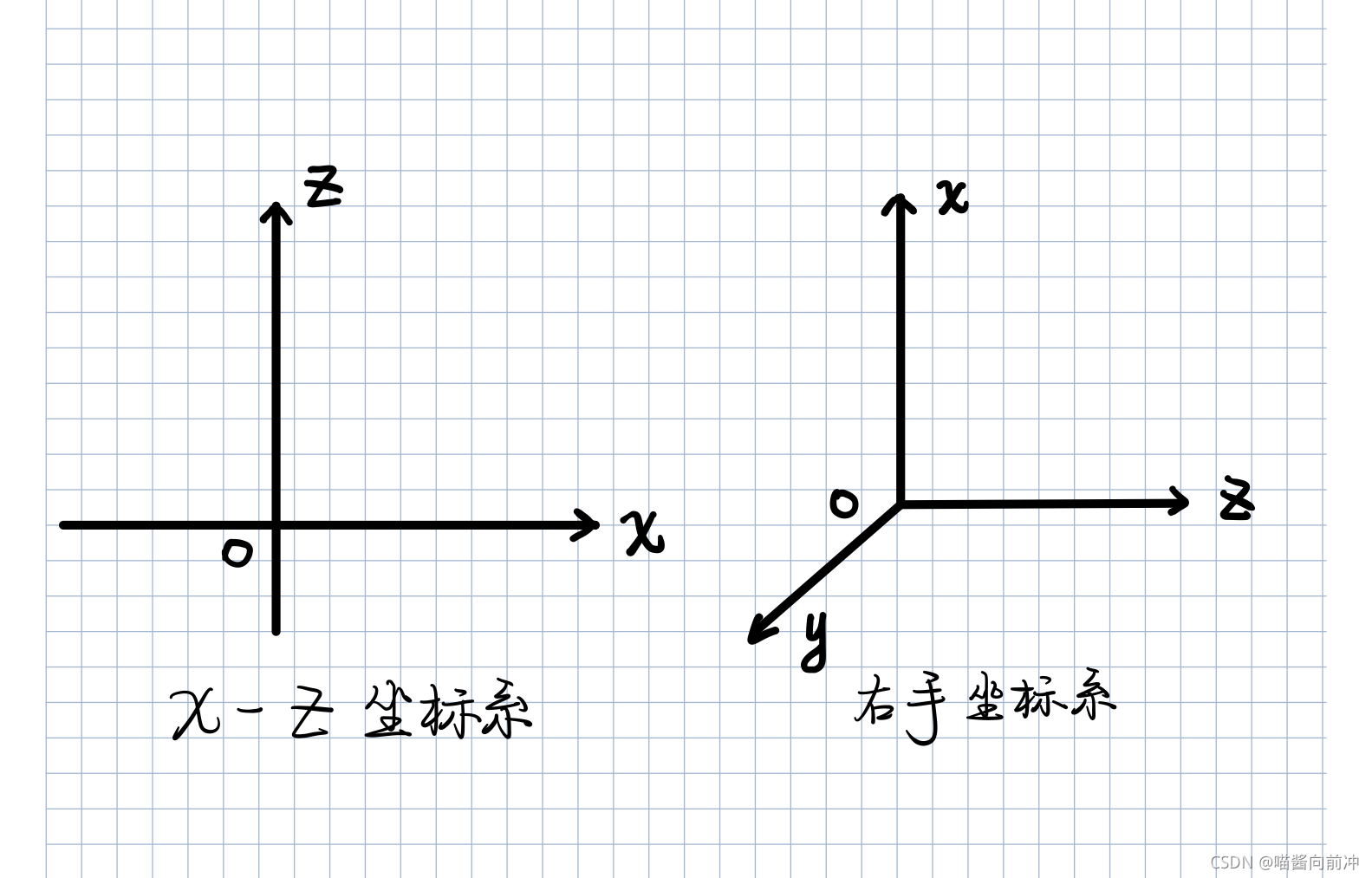
为何"正常的" R y ( α ) R_y(\alpha) Ry(α)是在以 x x x为横轴、 z z z为纵轴的坐标系下成立?
还记得一开始在2维平面直角坐标系下的旋转矩阵 R R R 吗?我们是以 x x x 为横轴、 y y y 为纵轴,后来推广至右手坐标系得到 R z ( α ) R_z(\alpha) Rz(α),也是同样成立。
如果这时候问你能不能由
R
z
(
α
)
R_z(\alpha)
Rz(α)试着写出
R
x
(
α
)
R_x(\alpha)
Rx(α)和
R
y
(
α
)
R_y(\alpha)
Ry(α)? 你可能会这么写:
R
x
(
α
)
=
[
1
0
0
0
0
c
o
s
α
−
s
i
n
α
0
0
s
i
n
α
c
o
s
α
0
0
0
0
1
]
、
R
y
(
α
)
=
[
c
o
s
α
0
−
s
i
n
α
0
0
1
0
0
s
i
n
α
0
c
o
s
α
0
0
0
0
1
]
R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}、R_y(\alpha) = \begin{bmatrix} cos\alpha & 0 & -sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ sin\alpha & 0 & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Rx(α)=
10000cosαsinα00−sinαcosα00001
、Ry(α)=
cosα0sinα00100−sinα0cosα00001
那么请问,这时候
R
y
(
α
)
R_y(\alpha)
Ry(α)是以什么为横轴、以什么为纵轴的?如果还不清楚,那我再换个写法:
[
x
′
y
′
z
′
1
]
=
[
c
o
s
α
0
−
s
i
n
α
0
0
1
0
0
s
i
n
α
0
c
o
s
α
0
0
0
0
1
]
×
[
x
y
z
1
]
\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} =\begin{bmatrix} cos\alpha & 0 & -sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ sin\alpha & 0 & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}
x′y′z′1
=
cosα0sinα00100−sinα0cosα00001
×
xyz1
与 R z ( α ) R_z(\alpha) Rz(α)对比着看,不难发现这里是以 x x x 为横轴、 z z z 为纵轴的。所以就是这样了~





















 4727
4727











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








