open-vins-学习记录1-imu静止初始化

我们一起摸爬叉

已于 2024-08-12 23:09:12 修改

阅读量369

点赞数 5

文章标签：学习

于 2024-08-01 20:37:21 首次发布

本文链接：https://blog.csdn.net/weixin_45088783/article/details/140856685

版权

1. 系统开始的地方：

// VioManager构造中开始搞事情
sys = std::make_shared<VioManager>(params);

uniformly: 均匀地

2. 使用imu数据进行初始化的核心部分

受这篇文章的启发（我是一个链接，可以点），所以我对其里面的核心部分进行展开。

2.1 为什么通过imu测得的加速度可以获得imu z轴在世界坐标系下的向量表示

这是重力加速度在世界系下的表示

在这里插入图片描述

这是imu测得的加速度在世界系下的表示

imu测得的原始加速度值（也就是上图中的三个分量）：
$acc=\begin{bmatrix} acc_x \\ acc_y \\ acc_z \\ \end{bmatrix}$

这也是世界坐标系的z轴方向在imu坐标系上的投影。

既然产生了投影分量，就说明imu的3个轴和世界坐标系的3个轴不是重合的。

你想想，如果重合的话，imu测得的值就该是[0.0, 0.0, 9.8]了（如果没bias）。

也就是说，此时imu在世界系下出现了一定的旋转（比如车辆有侧倾或俯仰）。

所以，我们就来求一下世界系和imu系之间的这个旋转矩阵：

有些旋转矩阵和向量的知识可从这里获得（可点我）

$R=\begin{bmatrix} x&y&z \end{bmatrix}$
注：这里的 $x$ $y$ $z$ 必须是单位向量，这样才能组成旋转矩阵（正交阵）。

先求z：
有了imu测得的加速度，把加速度向量单位化一下就得到了imu z轴的单位方向向量。对应的代码如下。

// StaticInitializer.cpp
Eigen::Vector3d z_axis = a_avg_2to1 / a_avg_2to1.norm();

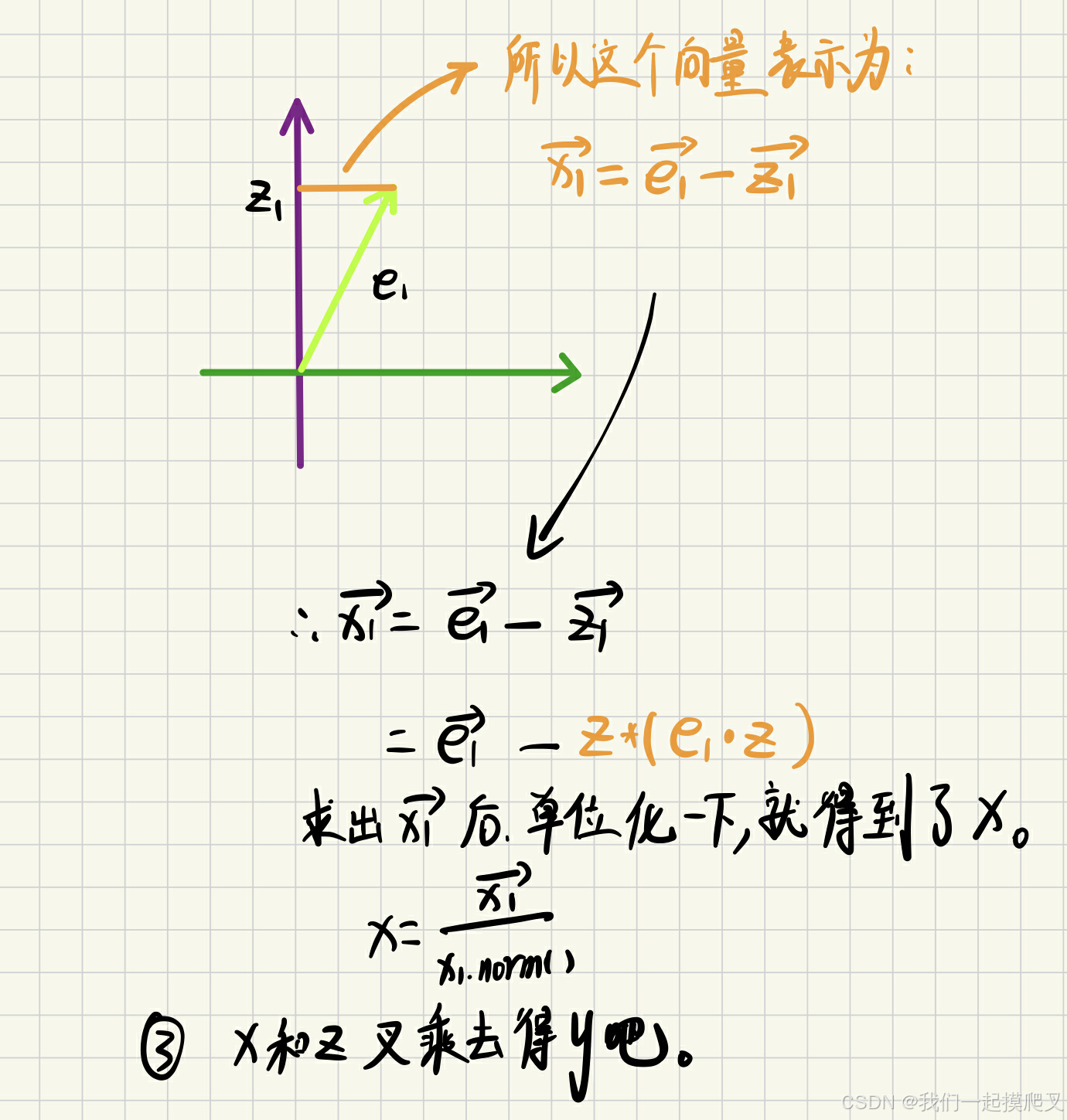
再求x：

这里就需要用到施密特正交化的知识，其实本质就是：已知了一个向量1，现在又有另一个向量2（2不能和1平行，可与1垂直或不垂直）。因为在咱们这里， $z$ 已经得出来了， $x$ 可以任意给一个，只要不和 $z$ 平行就行，然后利用施密特正交化求出与 $z$ 垂直的 $x$ 的分量，再使用叉乘方式求出 $y$ 即可。

接下来过一遍代码中的推导过程（相当于过了一遍施密特正交化的推导过程），先看看源码长什么样：

static void gram_schmidt(const Eigen::Vector3d &gravity_inI, Eigen::Matrix3d &R_GtoI) {

    // This will find an orthogonal vector to gravity which is our local z-axis
    // We need to ensure we normalize after each one such that we obtain unit vectors
    Eigen::Vector3d z_axis = gravity_inI / gravity_inI.norm();
    Eigen::Vector3d x_axis, y_axis;
    Eigen::Vector3d e_1(1.0, 0.0, 0.0);
    Eigen::Vector3d e_2(0.0, 1.0, 0.0);
    double inner1 = e_1.dot(z_axis) / z_axis.norm();
    double inner2 = e_2.dot(z_axis) / z_axis.norm();
    if (fabs(inner1) < fabs(inner2)) {
      x_axis = z_axis.cross(e_1);
      x_axis = x_axis / x_axis.norm();
      y_axis = z_axis.cross(x_axis);
      y_axis = y_axis / y_axis.norm();
    } else {
      x_axis = z_axis.cross(e_2);
      x_axis = x_axis / x_axis.norm();
      y_axis = z_axis.cross(x_axis);
      y_axis = y_axis / y_axis.norm();
    }

    // Original method
    // https://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process
    // x_axis = e_1 - z_axis * z_axis.transpose() * e_1;
    // x_axis = x_axis / x_axis.norm();
    // y_axis = ov_core::skew_x(z_axis) * x_axis;
    // y_axis = y_axis / y_axis.norm();

    // Rotation from our global (where gravity is only along the z-axis) to the local one
    R_GtoI.block(0, 0, 3, 1) = x_axis;
    R_GtoI.block(0, 1, 3, 1) = y_axis;
    R_GtoI.block(0, 2, 3, 1) = z_axis;
  }

即将要推导的是上面代码中的 $Original\ method$ 部分，不清楚作者为啥把这个方法屏蔽了，采用了上面的新方法，所以目前先推导自己理解的老方法（新方法还没看懂，懂者欢迎交流），目前看老方法也挺好用。

在这里插入图片描述
为了方便求解与z垂直的向量，把上面的向量暂时放到二维坐标系中，这样看着更直观一些。随意指定的 $x$ 并不是我们想要的 $x$ ，所以给它改名字叫做 $e 1$ 。

3. 补充

其实可以看出， $x$ 轴是自己任意指定的，所以每指定一个 $x$ 就对应一个 $R$ ，之前也提过，这个 $R$ 是imu测得的加速度和世界系下的加速度之间的一个旋转矩阵，所以每一个 $R$ 乘上imu的加速度之后，都应该能把imu本体系下的加速度转为[0.0, 0.0, 9.8]，写个python代码验证一下，确实是这样。。

在这里插入图片描述

这是我给了3个不同的x轴，得出的3个旋转矩阵

下面是我的python脚本：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys

def main():
    # 从命令行读取输入的向量
    if len(sys.argv) != 4:
        print("Usage: python generate_rotation_matrix.py <e1_x> <e1_y> <e1_z>")
        sys.exit(1)

    e1 = np.array([float(sys.argv[1]), float(sys.argv[2]), float(sys.argv[3])])

    # 1. 定义IMU测得的加速度向量
    acceleration = np.array([0.039023521, 0.218466725, 9.799889801])

    # 2. 计算加速度向量的范数
    acceleration_norm = np.linalg.norm(acceleration)
    
    # 3. 单位化加速度向量得到z轴向量
    z_axis = acceleration / acceleration_norm

    # 4. 计算x轴向量，使其垂直于z轴
    x_axis = e1 - z_axis * np.dot(z_axis, e1)
    x_axis = x_axis / np.linalg.norm(x_axis)  # 单位化x轴向量

    # 5. 计算y轴向量，通过x轴和z轴的叉积得到
    y_axis = np.cross(z_axis, x_axis)

    # 6. 构造旋转矩阵
    rotation_matrix = np.column_stack((x_axis, y_axis, z_axis))

    # 7. 计算旋转矩阵的转置
    rotation_matrix_T = rotation_matrix.T

    # 8. 计算旋转后的加速度向量
    rotated_acceleration = rotation_matrix_T @ acceleration

    # 打印结果
    print("Acceleration Vector:")
    print(acceleration)
    print("Acceleration Norm:")
    print(acceleration_norm)
    print("x_axis:", x_axis)
    print("y_axis:", y_axis)
    print("z_axis:", z_axis)
    print("Rotation Matrix:")
    print(rotation_matrix)
    print("Rotation Matrix Transpose:")
    print(rotation_matrix_T)
    print("Rotated Acceleration Vector:")
    print(rotated_acceleration)

    # 绘制向量
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')

    # 绘制坐标轴
    ax.quiver(0, 0, 0, x_axis[0], x_axis[1], x_axis[2], color='r', label='x-axis')
    ax.quiver(0, 0, 0, y_axis[0], y_axis[1], y_axis[2], color='g', label='y-axis')
    ax.quiver(0, 0, 0, z_axis[0], z_axis[1], z_axis[2], color='b', label='z-axis')

    # 设置图形的范围
    ax.set_xlim([-1, 1])
    ax.set_ylim([-1, 1])
    ax.set_zlim([-1, 1])

    # 设置标签
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')

    # 添加图例
    ax.legend()

    # 显示图形
    plt.show()

if __name__ == "__main__":
    main()

三张图分别对应的运行命令为：
python3 generate_rotation_matrix.py 1.0 0.0 0.0
python3 generate_rotation_matrix.py 1.0 1.0 -0.2
python3 generate_rotation_matrix.py -5.9 3.2 2.4