如何计算期望加速度?
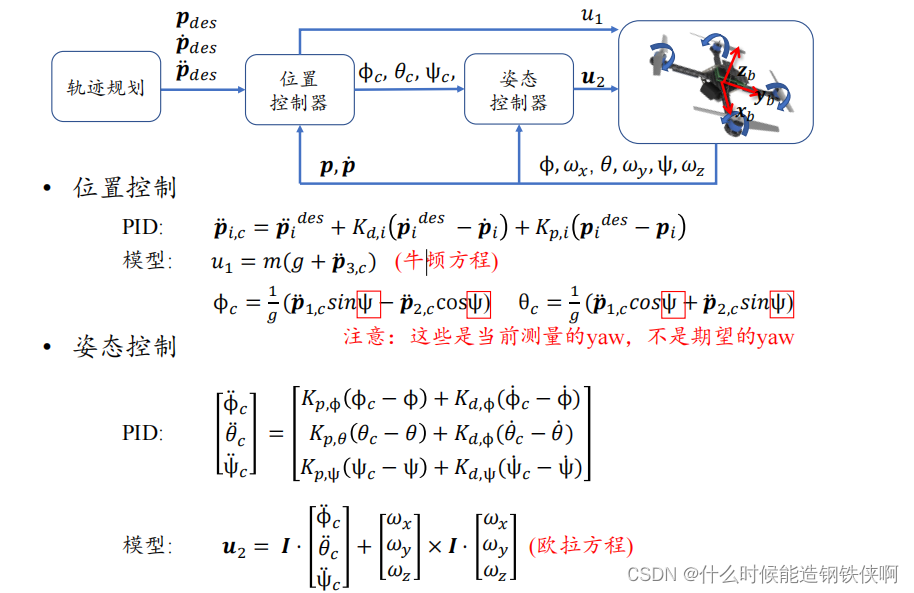
代码求期望加速度如下
des_acc = des.a + Kv.asDiagonal() * (des.v - odom.v) + Kp.asDiagonal() * (des.p - odom.p);//真实状态的p和v均来自于视觉里程计
des_acc += Eigen::Vector3d(0,0,param_.gra);
bool
LinearControl::estimateThrustModel(
const Eigen::Vector3d &est_a,
const Parameter_t ¶m)
{
ros::Time t_now = ros::Time::now();
while (timed_thrust_.size() >= 1)
{
// Choose data before 35~45ms ago
std::pair<ros::Time, double> t_t = timed_thrust_.front();
double time_passed = (t_now - t_t.first).toSec();
if (time_passed > 0.045) // 45ms
{
// printf("continue, time_passed=%f\n", time_passed);
timed_thrust_.pop();
continue;
}
if (time_passed < 0.035) // 35ms
{
// printf("skip, time_passed=%f\n", time_passed);
return false;
}
/***********************************************************/
/* Recursive least squares algorithm with vanishing memory */
/***********************************************************/
double thr = t_t.second;
timed_thrust_.pop();
/***********************************/
/* Model: est_a(2) = thr1acc_ * thr */
/***********************************/
double gamma = 1 / (rho2_ + thr * P_ * thr);//1/(0.998+10^6*thr^2)
double K = gamma * P_ * thr;//10^6*thr/(0.998+10^6*thr^2)
thr2acc_ = thr2acc_ + K * (est_a(2) - thr * thr2acc_);//Ax=b thr2acc_是x est_a(2)是b thr是A
P_ = (1 - K * thr) * P_ / rho2_;
//printf("%6.3f,%6.3f,%6.3f,%6.3f\n", thr2acc_, gamma, K, P_);
//fflush(stdout);
// debug_msg_.thr2acc = thr2acc_;
return true;
}
return false;
}
得到了期望的加速度,如何映射为发给PX4的油门的百分比?
Ax=b,其中thr是A,thr2acc_=a/percentage是x, imu估计的est_a(2)是b ,
t
h
r
=
m
(
g
+
a
z
)
thr= m(g + a_z)
thr=m(g+az),但是这里的g和m不准并且存在很多扰动,因此使用参数估计的方法来估计这个映射
t
h
r
2
a
c
c
thr2acc
thr2acc,计算Ax=b, 其中thr2acc_是x, est_a(2)是b, thr是A



x
k
=
(
A
k
T
A
k
+
λ
)
−
1
A
k
T
b
k
x_{k}=\left(A_{k}^{T} A_{k}+\lambda \right)^{-1} A_{k}^{T} b_{k}
xk=(AkTAk+λ)−1AkTbk
我们不必按照最小二乘法的公式进行计算,首先注意到:
A k T A k = [ A k − 1 T α k T ] [ A k − 1 α k ] = A k − 1 T A k − 1 + α k T α k A_{k}{ }^{T} A_{k}=\left[\begin{array}{ll} A_{k-1}{ }^{T} & \alpha_{k}{ }^{T} \end{array}\right]\left[\begin{array}{c} A_{k-1} \\ \alpha_{k} \end{array}\right]=A_{k-1}{ }^{T} A_{k-1}+\alpha_{k}{ }^{T} \alpha_{k} AkTAk=[Ak−1TαkT][Ak−1αk]=Ak−1TAk−1+αkTαk
由上式可得到结论 1 : 求
A
k
T
A
k
A_{k}{ }^{T} A_{k}
AkTAk不需要做
A
k
T
与
A
k
A_{k}{ }^{T} 与 A_{k}
AkT与Ak的矩阵乘法,只需要计算
α
k
T
α
k
(
α
k
\alpha_{k}{ }^{T} \alpha_{k} ( \alpha_{k}
αkTαk(αk的行数比
A
k
A_{k}
Ak小 很多),再加上上一轮的结果
A
k
−
1
T
A
k
−
1
A_{k-1}{ }^{T} A_{k-1}
Ak−1TAk−1即可,这是对
A
k
T
A
k
A_{k}{ }^{T} A_{k}
AkTAk 的递归求解。
第二,由于:
A k T b k = [ A k − 1 T α k T ] [ b k − 1 β k ] = A k − 1 T b k − 1 + α k T β k ⟶ yields x k = ( A k T A k ) − 1 ( A k − 1 T b k − 1 + α k T β k ) \begin{array}{c} A_{k}{ }^{T} b_{k}=\left[\begin{array}{ll} A_{k-1}{ }^{T} & \alpha_{k}{ }^{T} \end{array}\right]\left[\begin{array}{c} b_{k-1} \\ \beta_{k} \end{array}\right]=A_{k-1}^{T} b_{k-1}+\alpha_{k}{ }^{T} \beta_{k} \\ \stackrel{\text { yields }}{\longrightarrow} x_{k}=\left(A_{k}{ }^{T} A_{k}\right)^{-1}\left(A_{k-1}{ }^{T} b_{k-1}+\alpha_{k}{ }^{T} \beta_{k}\right) \end{array} AkTbk=[Ak−1TαkT][bk−1βk]=Ak−1Tbk−1+αkTβk⟶ yields xk=(AkTAk)−1(Ak−1Tbk−1+αkTβk)
由于k-1轮的结果满足: x k − 1 = ( A k − 1 T A k − 1 + λ ) − 1 A k − 1 T b k − 1 x_{k-1}=\left(A_{k-1}^{T} A_{k-1}+\lambda \right)^{-1} A_{k-1}^{T} b_{k-1} xk−1=(Ak−1TAk−1+λ)−1Ak−1Tbk−1 ,可得
( A k − 1 T A k − 1 + λ ) x k − 1 = A k − 1 T b k − 1 x k = ( A k T A k ) − 1 ( ( A k − 1 T A k − 1 + λ ) x k − 1 + α k T β k ) \begin{array}{c} (A_{k-1}{ }^{T} A_{k-1}+\lambda )x_{k-1}=A_{k-1}{ }^{T} b_{k-1} \\ x_{k}=\left(A_{k}{ }^{T} A_{k}\right)^{-1}\left((A_{k-1}^{T} A_{k-1}+\lambda ) x_{k-1}+\alpha_{k}{ }^{T} \beta_{k}\right) \end{array} (Ak−1TAk−1+λ)xk−1=Ak−1Tbk−1xk=(AkTAk)−1((Ak−1TAk−1+λ)xk−1+αkTβk)
再把 A k T A k − α k T α k = A k − 1 T A k − 1 A_{k}^{T} A_{k}-\alpha_{k}{ }^{T} \alpha_{k}=A_{k-1}{ }^{T} A_{k-1} AkTAk−αkTαk=Ak−1TAk−1 代入,得到 x k x_{k} xk 的递归求解:
x k = ( A k T A k + λ ) − 1 ( ( A k T A k − α k T α k + λ ) x k − 1 + α k T β k ) = ( I − ( A k T A k + λ ) − 1 α k T α k ) x k − 1 + ( A k T A k + λ ) − 1 α k T β k = x k − 1 + ( A k T A k + λ ) − 1 α k T ( β k − α k x k − 1 ) \begin{array}{c} x_{k}=\left(A_{k}{ }^{T} A_{k}+\lambda\right)^{-1}\left(\left(A_{k}{ }^{T} A_{k}-\alpha_{k}{ }^{T} \alpha_{k}+\lambda \right) x_{k-1}+\alpha_{k}{ }^{T} \beta_{k}\right) \\ =\left(I-\left(A_{k}{ }^{T} A_{k}+\lambda\right)^{-1} \alpha_{k}{ }^{T} \alpha_{k}\right) x_{k-1}+\left(A_{k}{ }^{T} A_{k}+\lambda\right)^{-1} \alpha_{k}{ }^{T} \beta_{k} \\ =x_{k-1}+\left(A_{k}{ }^{T} A_{k}+\lambda\right)^{-1} \alpha_{k}{ }^{T}\left(\beta_{k}-\alpha_{k} x_{k-1}\right) \end{array} xk=(AkTAk+λ)−1((AkTAk−αkTαk+λ)xk−1+αkTβk)=(I−(AkTAk+λ)−1αkTαk)xk−1+(AkTAk+λ)−1αkTβk=xk−1+(AkTAk+λ)−1αkT(βk−αkxk−1)
注意,
A
k
T
A
k
A_{k}{ }^{T} A_{k}
AkTAk 是递归求解得出的。每一轮都不涉及大规模的矩阵乘法。
视频地址
Ax=b thr2acc_是x est_a(2)是b thr是A 给无人机一个推力,实际无人机对应一个什么样的加速度





















 1242
1242











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








