《智能控制技术》学习笔记-2.1，模糊集合论基础、模糊逻辑、模糊逻辑推理和合成

一、模糊集的概念

普通集合-----现代数学的基础； 模糊集合-----模糊数学的基础

论域：通常我们在处理某一问题时，总是把议题限制 在某一个范围内，称此“范围”为相应问题的论域。 设 是论域 上的一个集合，对任意 ，令

        则称 为集合A的特征函数，特征函数 在u= 处的取值  称为 对A的隶属度。

Tip：对任意一个集合A都有唯一确定的一个特征函数与之对应， 同时任一特征函数都唯一确定了一个集合。所以集合A与特征函数是等价的，集合A就是其特征函数值等于1的元素所构成的集合。

模糊集合概念：

        设U是论域， 是把任意 映射为[0，1]上某 个值的函数，即

        uF ：U->[0,1]                                   =1  表示u完全属于 F

                        u->                              =0  表示u完全不属于 F

                                                              0< <1  表示u部分属于 F

        则称 为定义在U上的一个隶属函数，由 所构成的集合F称为U上的一个模糊集， 称为u对 F的隶属度。

 

二、模糊集合的运算

定义：模糊集A的一般表达形式：

 

 

 

 

三、隶属度函数的建立

建立隶属度函数的基本原则：

        ⑴表示隶属度函数的模糊集合必须是凸模糊集合。

        ⑵变量所取隶属函数通常是对称和平衡的。

        ⑶隶属函数要符合人们的语义顺序，避免不恰当的重叠。

        ⑷论域中的每个点应该至少属于一个隶属函数的区域。

        ⑸同一输入没有两个隶属函数会同时有最大隶属度。

        ⑹当两个隶属度函数重叠时重叠部分对两个隶属度函数 的最大隶属度不应该有交叉

四、模糊逻辑、模糊逻辑推理和合成

        模糊逻辑是研究含有模糊概念或带有模糊 性的陈述句的逻辑。

        模糊逻辑推理是不确定性推理方法的一种， 其基础是模糊逻辑，它是在二值逻辑三段论的 基础上发展起来的。

4.1 二值逻辑

        （1）命题 具有真假意义的语句称为命题，真假两者必居其一且只居 其一。一个简单句子构成的命题称简单命题。把两个或两个 以上的命题用命题联结词联结起来就称为复合命题。可以表 示更复杂的内容。

        （2）逻辑联结词

蕴涵 ->表示“如果 ，那么 ”。即如果命题P成立， 则命题Q也成立。

等价 <->表示两个命题的真假相同。是“当且仅当”的意思

4.2 模糊逻辑及其基本运算

模糊逻辑是研究模糊命题的逻辑，而模糊命题是指含有 模糊概念或者是带有模糊性的陈述句。模糊命题的真值不是 绝对的“真”或“假”，而是反映其以多大程度隶属于 “真”，模糊命题的真值就是隶属（度）函数。所以真值的 运算也就是隶属函数的运算。

4.3 基本运算：

 记P、Q、R为三个模糊单命题，那么

1、模糊逻辑补（非）

2、模糊逻辑合取（与）

3、模糊逻辑析取（或）

 

4.4 模糊逻辑及其基本运算

        根据以上模糊逻辑的基本运算定义，可以得出以下 模糊逻辑运算的基本定律： 幂等律、交换律、结合律、吸收律、分配律 双否律、德﹒摩根律、常数运算法则 注：与二值逻辑不同之处是二值逻辑中的互补律。

4.5模糊语言逻辑

模糊语言逻辑是由模糊语句构成的一种模拟人思维的逻 辑，模糊语言可以对自然语言的模糊性进行分析和处理。

几个重要概念:

        1.模糊数：连续论域（实数域）U中的一个模糊数F是一个U 上的正规凸模糊集。 “大约5” 、 “10左右”

        2.正规集合的含义是隶属度函数的最大值为1；

        3.凸模糊集：在隶属度函数曲线上任意两点之间曲线上的任 一点所表示的隶属度的值都大于或等于两点隶属度值中较小 的一个。

        4.语言值： 在语言系统中那些与数值有直接联系的词，如： 长、短、多、少、高、低、重、清、大、小等，或者由它们 再加上语言算子（如：很、非常、较、偏等）而派生出来的 词组，如：不太大、非常高、偏重等都被称为语言值。语言值一般是模糊的，可以用模糊数来表示。

4.6 模糊语言逻辑

定义：语言变量是用一个五元素的集合（X、T(X)、U、 G、M ）来表征的。

        X：语言变量的名称；

        T(X)：语言变量所包含语言值名称的集合（每个语言 值都是定义在U上的模糊集；

        U：语言变量X 的论域；

        G：语法规则，产生X 的语言值规则；

        M：指模糊子集的隶属度函数

 

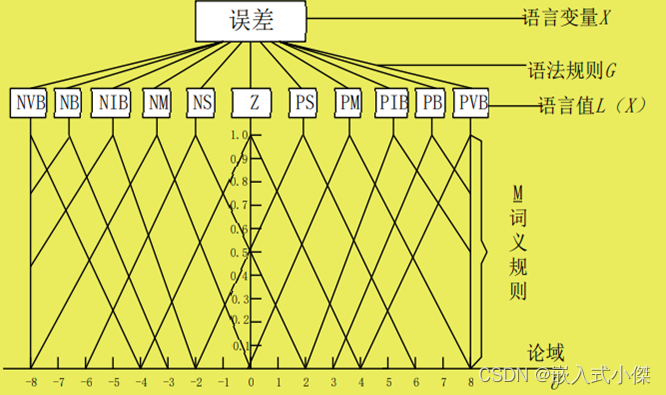
（2）语言算子分类           

        “很”、“较”、“非常”、“大约”、“有点”

 1.语气算子  

       “集中化算子” ：——“很” 、 “极” 、 “非常” 、 “十 分” 、 “特别” （强化算子）

        “松散化算子”——“比较” 、 “微” 、 “稍许” 、 “有 点” 、 “略”

 2.模糊化算子

 3.判定化算子

       判定化模糊为趋向于清晰 “偏向”、“大半是”、

4.7 模糊逻辑推理

        主要不确定性推理方法有：MYCIN法、主观贝 叶斯方法、证据理论法和模糊逻辑推理法。 模糊逻辑推理是不确定性推理方法的一种，其基础是 模糊逻辑。模糊逻辑推理是以模糊判断为前提的，运用模 糊语言规则，可推出一个新的模糊判断结论的方法。

       模糊逻辑推理方法有：扎德（Zadeh）方法、玛达尼 （Mamdani）方法、鲍德温（Baldwin）方法、耶格 （Yager）方法、楚卡莫托（Tsukamoto）方法。