
LR-GCCF
1. Abstract
-
基于GCN推荐模型的问题:
- 基于GCN的推荐模型带有非线性激活函数,所以在large user-item graphs中的模型训练起来非常困难。
- 由于图卷积运算的过度平滑效应都不能太深,大多数基于GCN的模型无法对更深层次进行建模。
-
本文的优化:
- 证明了去除非线性会提高推荐性能,在每一层的特征传播的时候,是使用简单的特征传播而不是非线性变换
- 提出了一种残差网络结构,该结构是专门为CF设计的,具有用户项交互建模功能,可以缓解稀疏用户项交互数据的图卷积聚合操作中的过度平滑问题
2. Introduction
通过在每层中增加残差连接,用户的独特性将会在底层中被保留,高层的GCN可以关注学习用户的剩余偏好(user’s residual preferences),这可以在每个用户的有限的历史中被捕获(这种思想来源于ResNet)
3. LR-GCCF
3.1 模型总体结构(Overall Structure of the Proposed Model)
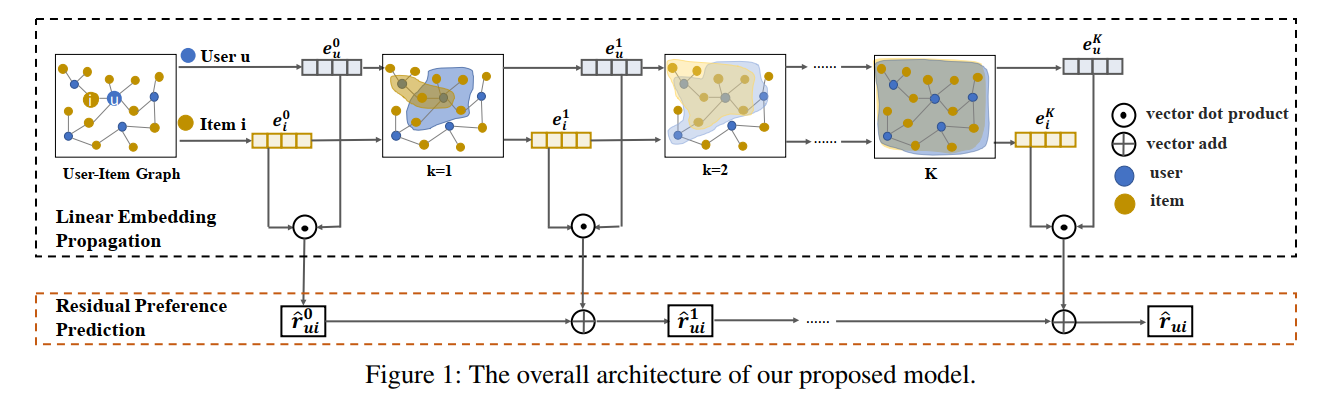
令用户-项目交互矩阵 R ∈ R M × N R\in R^{M\times N} R∈RM×N,其中M和N分别表示用户数量和项目数量,如果 u u u与 i i i交互,则 R u i R_{ui} Rui 为1,否则为0。然后得到用户-项图的邻接矩阵为 A ∈ R ( M × N ) × ( M × N ) A\in R^{(M\times N)\times(M\times N)} A∈R(M×N)×(M×N),不同于论文,我觉得应该由以下形式更为准确(如理解有误,欢迎指正),在《LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation》中也是如下的形式:
A = [ R 0 N × M 0 M × N R T ] \large A = \left[ \begin{array} { l l } { R } & { 0 ^ { N \times M } } \\ { 0 ^ { M \times N } } & { R ^ { T } } \end{array} \right] A=[R0M×N0N×MRT]
用户和物品的大图,其中类似于NGCF中的思想,将用户和物品单独抽象出来进行嵌入表示,创新的地方在于每一层的用户和物品嵌入单独拿出来做了一个向量点乘作为每一层嵌入的残差项,在层与层之间残差项通过向量加不断迭代。
3.2 线性嵌入传播(Linear Embedding Propagation)
-
E [ 1 : M ] E_{[1:M]} E[1:M] 代表用户嵌入矩阵, E [ M + 1 : M + N ] E_{[M+1:M+N]} E[M+1:M+N]代表物品的嵌入矩阵,将二者整合到一个大矩阵中 E E E作为嵌入输入,即: E 0 = E E_0=E E0=E
Notably, different from GCN based tasks with node featuresas fixed input data, the embedding matrix is unknown and needs to be trained in LR-GCCF
和把节点特征当成输入的基于GCN的任务不同,是通过LR-GCCF模型学习得到的嵌入向量表示
-
之后的传播过程,借鉴SGCN,采取线性嵌入传播
E k + 1 = S E k W k (8) \large E ^ { k + 1 } = S E ^ { k } W ^ { k } \tag{8} Ek+1=SEkWk(8)
其中 S = D ~ − 0.5 A ~ D ~ − 0.5 S = \widetilde{D}^{-0.5}\widetilde{A}\widetilde{D}^{-0.5} S=D −0.5A D −0.5代表了归一化并加上自环的邻接矩阵( A ~ \widetilde{A} A 代表矩阵 A A A加上自环)
对于每个用户和物品,传播的矩阵形式:
[ E k + 1 ] u = e k + 1 = [ 1 d u e u k + ∑ j e k u k d j × d e k ] W k (9) \large [ E ^ { k + 1 } ] _ { u } = e ^ { k + 1 } = [ \frac { 1 } { d u } e _ { u } ^ { k } + \sum _ { j e k u } ^ { k } d _ { j \times d } e ^ { k } ] W ^ { k } \tag{9} [Ek+1]u=ek+1=[du1euk+jeku∑kdj×dek]Wk(9)
[ E k + 1 ] i = e k + 1 = [ 1 d i e i k + ∑ u < k k 1 d i ⋅ e i k u i W k (10) \large [ E ^ { k + 1 } ] _ { i } = e ^ { k + 1 } = [ \frac { 1 } { d _ { i } } e _ { i } ^ { k } + \sum _ { u \lt k } ^ { k } \frac { 1 } { d i } \cdot e _ { i } ^ { k } u _ { i } W ^ { k } \tag{10} [Ek+1]i=ek+1=[di1eik+u<k∑kdi1⋅eikuiWk(10)
其中 d i ( d u ) d i ( d u ) di(du)代表在用户项目二分图中的item i i i (user u u u)的diagonal degree , R ∗ R_* R∗代表 * 在图 G \mathcal{G} G中的邻居节点
3.3 残差偏好预测(Residual Preference Prediction)
在经过k层的GCN之后,输出嵌入矩阵 E K E_K EK, e u K ( e i K ) e_u^K(e_i^K) euK(eiK)是捕获到K阶二部图相似性。很多推荐模型会把点积作为预测 r u i r_{ui} rui
r u i = < e u K , e i K > (11) r _ { u i } = \lt e _ {u} ^ {K} , e _ {i} ^ {K} \gt \tag{11} rui=<euK,eiK>(11)
作者通过实验说明很多基于GCN的变体随着层数的加深可能导致过平滑现象(特别是大于3层后),为缓解这一问题,提出了残差偏好学习(residual preference learning):
i u i k + 1 = i u i k + < e k + 1 , e i k + 1 > (12) \large i _ { u i } ^ { k + 1 } = i ^ { k } _ { u i } + \lt e ^ { k + 1 } , e _ { i } ^ { k + 1 } \gt \tag{12} iuik+1=iuik+<ek+1,eik+1>(12)
通过每一层的嵌入,(13)使得最后一层的模型获取更多的信息:
r ^ u i = r ^ u i K − 1 + < e u K , e i K > = r ^ u i K − 2 + < e u K − 1 , e i K − 1 > + < e u K , e i K > = r ^ u i 0 + < e u 1 , e i 1 > + … + < e u K , e i K > = < e u 0 ∥ e u 1 ∥ … ∥ e u K , e i 0 ∥ e i 1 ∥ … ∥ e i K > (13) \large \begin{aligned} \hat{r}_{u i} &=\hat{r}_{u i}^{K-1}+<\mathbf{e}_{u}^{K}, \mathbf{e}_{i}^{K}>\\ &=\hat{r}_{u i}^{K-2}+<\mathbf{e}_{u}^{K-1}, \mathbf{e}_{i}^{K-1}>+<\mathbf{e}_{u}^{K}, \mathbf{e}_{i}^{K}>\\ &=\hat{r}_{u i}^{0}+<\mathbf{e}_{u}^{1}, \mathbf{e}_{i}^{1}>+\ldots+<\mathbf{e}_{u}^{K}, \mathbf{e}_{i}^{K}>\\ &=<\mathbf{e}_{u}^{0}\left\|\mathbf{e}_{u}^{1}\right\| \ldots\left\|\mathbf{e}_{u}^{K}, \quad \mathbf{e}_{i}^{0}\right\| \mathbf{e}_{i}^{1}\|\ldots\| \mathbf{e}_{i}^{K}>\end{aligned} \tag{13} r^ui=r^uiK−1+<euK,eiK>=r^uiK−2+<euK−1,eiK−1>+<euK,eiK>=r^ui0+<eu1,ei1>+…+<euK,eiK>=<eu0∥∥∥eu1∥∥∥…∥∥∥euK,ei0∥∥∥ei1∥…∥eiK>(13)
3.4 模型学习(Model Learning)
把线性嵌入传播方程(Eq.(8))加入到残差预测函数的向量表示中(Eq.(14)),得到:
r ^ u i = < e u 0 ∥ e u 1 ∥ … ∥ e u K , e v 0 ∥ e v 1 ∥ … ∥ e v K > = < [ E 0 ] u ∥ … ∥ [ S K E 0 W 0 … W K ] u [ E 0 ] i ∥ … ∥ [ S K E 0 W 0 … W K ] i > = < [ E 0 ] u ∥ … ∥ [ S K E 0 Y K ] u , [ E 0 ] i ∥ … ∥ [ S K E 0 Y K ] i > (14) \begin{aligned} \hat{r}_{u i}=&<\mathbf{e}_{u}^{0}\left\|\mathbf{e}_{u}^{1}\right\| \ldots\left\|\mathbf{e}_{u}^{K}, \quad \mathbf{e}_{v}^{0}\right\| \mathbf{e}_{v}^{1}\|\ldots\| \mathbf{e}_{v}^{K}>\\=&<\left[\mathbf{E}^{0}\right]_{u}\|\ldots\|\left[\mathbf{S}^{K} \mathbf{E}^{0} \mathbf{W}^{0} \ldots \mathbf{W}^{K}\right]_{u} \\ &\left[\mathbf{E}^{0}\right]_{i}\|\ldots\|\left[\mathbf{S}^{K} \mathbf{E}^{0} \mathbf{W}^{0} \ldots \mathbf{W}^{K}\right]_{i}>\\=&<\left[\mathbf{E}^{0}\right]_{u}\|\ldots\|\left[\mathbf{S}^{K} \mathbf{E}^{0} \mathbf{Y}^{K}\right]_{u}, \quad\left[\mathbf{E}^{0}\right]_{i}\|\ldots\|\left[\mathbf{S}^{K} \mathbf{E}^{0} \mathbf{Y}^{K}\right]_{i}>\end{aligned} \tag{14} r^ui===<eu0∥∥eu1∥∥…∥∥euK,ev0∥∥ev1∥…∥evK><[E0]u∥…∥[SKE0W0…WK]u[E0]i∥…∥[SKE0W0…WK]i><[E0]u∥…∥[SKE0YK]u,[E0]i∥…∥[SKE0YK]i>(14)
其中
Y
K
\mathbf{Y^K}
YK代表
Y
K
=
W
0
W
1
.
.
.
W
K
\mathbf{Y^K=W^0W^1...W^K}
YK=W0W1...WK为线性模型,
S
K
\mathbf{S^K}
SK代表
K
K
K层的
S
\mathbf{S}
S
由于基于隐式反馈,所以采用BPR中基于成对排序的损失函数为
min Θ L ( R , R ^ ) = ∑ a = 1 M ∑ ( i , j ) ∈ D a − ln ( s ( r ^ a i − r ^ a j ) ) + λ ∥ Θ 1 ∥ 2 (15) \min _{\Theta} \mathcal{L}(\mathbf{R}, \hat{\mathbf{R}})=\sum_{a=1}^{M} \sum_{(i, j) \in D_{a}}-\ln \left(s\left(\hat{r}_{a i}-\hat{r}_{a j}\right)\right)+\lambda\left\|\Theta_{1}\right\|^{2} \tag{15} ΘminL(R,R^)=a=1∑M(i,j)∈Da∑−ln(s(r^ai−r^aj))+λ∥Θ1∥2(15)
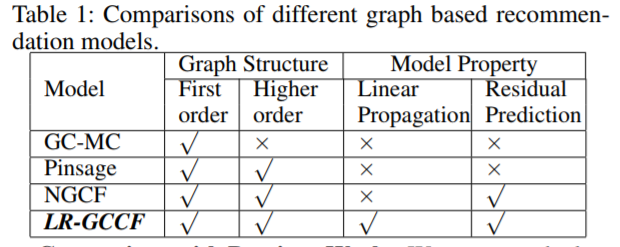
4.模型对比






















 2826
2826











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








