【EI复现】基于主从博弈的新型城镇配电系统产消者竞价策略【IEEE33节点】(Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147799066

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于主从博弈的新型城镇配电系统产消者竞价策略研究

一、研究背景与意义

二、主从博弈模型的理论基础

三、新型城镇配电系统的特点与挑战

四、产消者竞价策略的模型构建

五、典型应用与实证分析

六、未来研究方向

七、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章

💥1 概述

本文采用SFE模型对产消者竞价行为建模,确立了含多产消者的新型城镇配电系统日前现货市场交易机制,建立了含竞价博弈和优化调度的双层模型。上层模型追求产消者利润最大化,可确定多个产消者在配电网内的最优报价策略,下层模型考虑运行安全约束以及用户参与DR对系统进行最优经济调度﹐确定市场出清价格。最后﹐采用改进粒子群优化算法与(CPLEX求解器相结合的方法对该多主从博弈模型进行求解。

基于主从博弈的新型城镇配电系统产消者竞价策略研究

一、研究背景与意义

随着分布式能源（DG）的大规模接入和新型电力系统的建设，传统配电系统正逐步向主动配电系统（Active Distribution System, ADS）转型。新型城镇配电系统作为新型电力系统在中低压配电网的体现，具有能源供给清洁化、网架结构柔性化、用户负荷互动化等特点。产消者（Prosumer）作为既能生产又能消费能源的主体，在新型配电系统中扮演了关键角色。然而，产消者的分散性和利益诉求多样性对市场机制设计提出了挑战，而主从博弈（Stackelberg Game）因其能够有效描述领导者与跟随者的动态博弈关系，成为解决此类问题的核心工具。

二、主从博弈模型的理论基础

模型结构与分类
主从博弈是一种双层优化模型，上层领导者（如配电运营商）优先制定策略（如电价、服务套餐），下层跟随者（如产消者、微电网）根据上层策略调整自身行为（如用能计划、储能调用）。根据博弈者数量可分为：
- 一主一从：如配电运营商与单一产消者集群的博弈。
- 一主多从：如虚拟电厂运营商与多产消者的互动。
- 多主多从：适用于多微电网系统的协同优化。
数学特性与求解方法
主从博弈模型通常具有非线性或非凸特性，需采用鲁棒优化处理不确定性（如风电出力波动），并结合智能算法（如改进教与学算法、粒子群优化）与数学规划工具（如CPLEX）嵌套求解。例如，文献[33]通过改进粒子群算法与CPLEX联合求解双层竞价模型，实现了产消者报价策略与系统调度的协同优化。

三、新型城镇配电系统的特点与挑战

系统特征
- 能源结构：以分布式新能源为主体，结合储能、柔性负荷等多要素。
- 网架形态：交直流混联、多端多环的柔性互联网络，支持双向潮流。
- 用户角色：产消者占比提升，具备需求响应（DR）能力与市场议价权。
核心挑战
- 不确定性管理：分布式电源出力波动、用户响应行为随机性需通过鲁棒优化或分布鲁棒机会约束处理。
- 利益协调：需平衡配电运营商的经济性目标（如运行成本最小化）与产消者的收益最大化诉求。

四、产消者竞价策略的模型构建

双层优化框架
- 上层模型：配电运营商以系统运行成本最低或灵活性需求满足为目标，制定电价或市场规则。例如，通过动态定价引导产消者调整用电计划。
- 下层模型：产消者基于上层策略优化自身竞价行为，包括：

报价策略：通过供给函数均衡（SFE）模型确定最优报价曲线。
能量管理：考虑分布式发电、储能调度及负荷灵活性。

关键约束条件
- 物理约束：配电网潮流安全、电压稳定。
- 市场约束：电价上下限、交易量限制。
- 行为约束：产消者的响应意愿与风险偏好。

五、典型应用与实证分析

案例1：IEEE 33节点系统仿真
文献[26]构建了含多产消者的双层主从博弈模型，通过日前市场交易机制验证了策略有效性。结果显示：
- 经济性：系统总成本降低12%-15%，产消者收益提升10%以上。
- 稳定性：通过鲁棒优化将风电出力区间扩大20%，增强系统抗扰动能力。
案例2：农灌园区互动协调
文献[27]以148节点系统为测试场景，通过分时电价引导农灌园区优化灌溉用电。结果表明：
- 峰谷差削减：负荷峰均比下降18%。
- 双赢效益：配电运营商运行成本减少8%，园区用电成本降低12%。
案例3：虚拟电厂能量共享
文献[37]提出虚拟电厂运营商与产消者的混合博弈策略，结合动态电价与分布鲁棒优化，实现：
- 灵活性提升：可调节负荷控制能力达区域最大负荷的20%。
- 收益分配：产消者通过内部交易获利，运营商收益增长9%。

六、未来研究方向

模型扩展
- 纳入碳交易机制与条件风险值（CVaR），量化低碳目标与市场风险。
- 探索多时间尺度（日前-实时-日内）协同优化。
算法创新
- 结合深度学习与博弈论，预测产消者行为并动态调整策略。
- 开发完全去中心化的ADMM算法，保护隐私的同时提升计算效率。
政策与市场设计
- 设计适应P2P交易的监管框架，推动产消者社区自治。
- 完善灵活性资源（如储能）的市场化定价机制。

七、结论

基于主从博弈的产消者竞价策略通过动态定价、鲁棒优化与分布式算法，有效协调了新型城镇配电系统中多方主体的利益冲突，提升了系统经济性与灵活性。未来需进一步结合新型电力系统的发展需求，深化多市场耦合机制与智能化决策方法的研究，为“双碳”目标下的能源转型提供技术支撑。

📚2 运行结果

改进粒子群算法：

部分代码：

function [Gi,F,P_g,P_d,fi] = Up_fitnessfun(pop,index)
% clc
% clear
% pop = [60.03;75.03;69.31];
% index = 1;
%% 读取数据
parameters; % 读取相关参数
[P_d, fi, F, ~, ~, ~] = Down_fitnessfun(pop,index);
P_d = P_d/SB; % 转为标幺值
if index == 1
P_g = P_d + P_r(:,8) - P_l8'; % T=8时刻产销者出力
elseif index == 2
P_g = P_d + P_r(:,15) - P_l15'; % T=15时刻产销者出力
end
P_g = P_g*SB; % 转为实际值

Ci = a_D'.*(P_d.^2) + b_D'.*P_d + c_D';
Gi = fi.*P_g - s*P_g - Ci;
end

%% 1.粒子群算法迭代情况
disp(['运行时间为：',num2str(time0) , '秒'])
disp(['最优适应度值=',num2str(fitness_zbest)])

figure
plot(history_pso,'linewidth',1)
ylabel('最优适应度值')
xlabel('迭代次数')

%% 2.产销者竞价策略
[Gi,F,P_g,P_d,fi] = Up_fitnessfun(pop_zbest,index);
P_d = P_d*SB;
a_G = pop_zbest;
disp('********************产销者竞价策略********************')
for k =1:Nk
fprintf('产销者%d：\naG = %.2f Pg = %.2fMW Gi = %.2f美元 Pd = %.2fMW fi = %.2f美元\n',k,a_G(k),P_g(k),Gi(k),P_d(k),fi(k))
end

%% 3.支路网损
[~, ~, ~, P_loss, dP_cj, Uj] = Down_fitnessfun(pop_zbest,index);
P_loss = P_loss(1:32)*SB*1e3;
figure
plot(P_loss,'linewidth',1)
xlabel('支路编号')
ylabel('线路损耗/kW')

%% 4.节点电压
figure
plot(Uj,'linewidth',1)
xlabel('节点编号')
ylabel('节点电压幅值/pu')

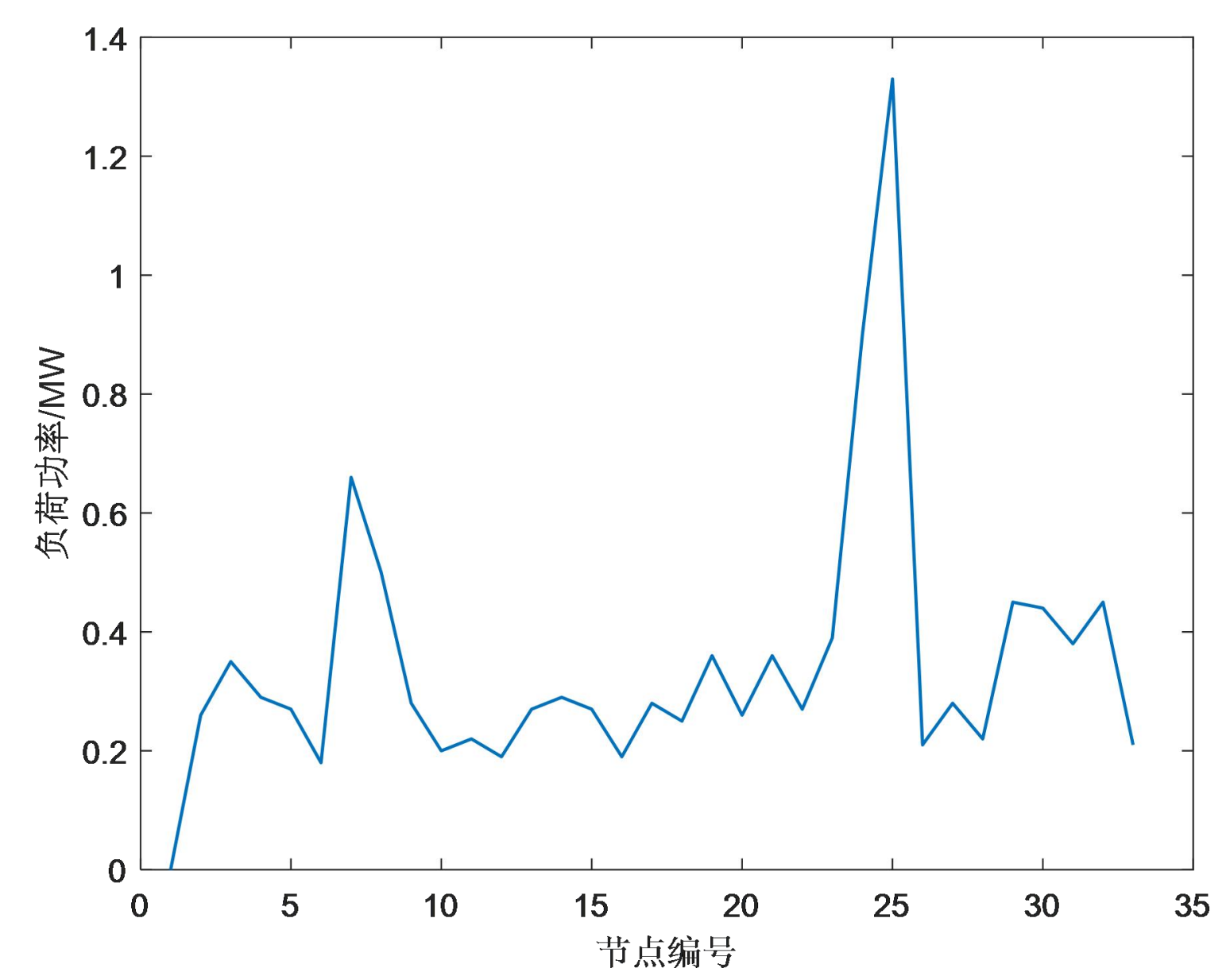
%% 5.负荷曲线
figure
if index == 1
plot(PL8*SB,'linewidth',1)
elseif index == 2
plot(PL15*SB,'linewidth',1)
end
xlabel('节点编号')
ylabel('负荷功率/MW')

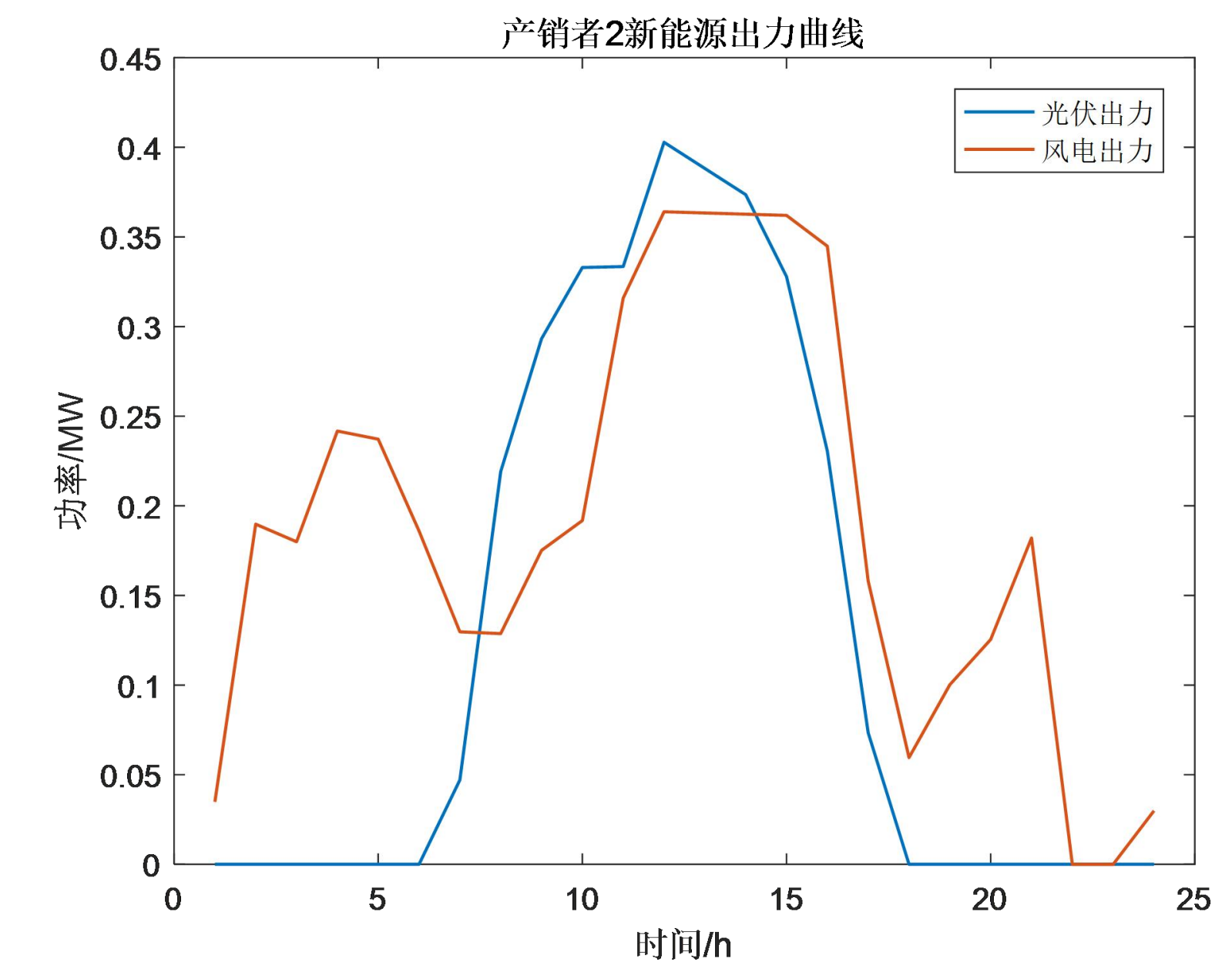
%% 6.产销者新能源出力
for k = 1:Nk
figure
plot(Ppv(k,:)*SB,'linewidth',1)
hold on
plot(Pwt(k,:)*SB,'linewidth',1)
xlabel('时间/h')
ylabel('功率/MW')
legend('光伏出力','风电出力')
title(['产销者',num2str(k),'新能源出力曲线'])
end