有限长度直导线的三维磁场计算：应用毕奥-萨法尔定律（Matlab代码实现）

最新推荐文章于 2025-05-11 17:56:51 发布

荔枝科研社

最新推荐文章于 2025-05-11 17:56:51 发布

阅读量669

点赞数 31

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147815756

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、毕奥-萨伐尔定律的数学表达式

二、有限长度直导线的磁场积分推导

三、数值计算方法与离散化处理

四、三维磁场矢量叠加原理

五、与安培环路定律的对比及适用性

六、应用案例与文献分析

七、总结与拓展

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

对于有限长度直导线的三维磁场计算，我们可以应用毕奥-萨法尔定律。毕奥-萨法尔定律描述了电流元产生的磁场，可以用来计算有限长度直导线产生的磁场。

首先，我们需要确定有限长度直导线的电流分布。假设有限长度直导线的电流分布为I(x)，其中x为直导线上的位置变量。

然后，我们可以使用毕奥-萨法尔定律来计算有限长度直导线在某一点产生的磁场。毕奥-萨法尔定律可以表示为：

\[ B(r) = \frac{\mu_0}{4\pi} \int \frac{I(x) \times (r-r')}{|r-r'|^3} dx \]

其中，B(r)表示在点r处的磁场强度，r'为直导线上的位置变量，μ0为真空磁导率。

通过对有限长度直导线上所有电流元的贡献进行积分，我们可以计算出有限长度直导线产生的磁场分布。

需要注意的是，在实际计算中，可能需要对有限长度直导线进行离散化处理，将其划分为若干小段来进行计算。此外，还需要考虑有限长度直导线的几何形状和电流分布对磁场的影响。

在这个过程中，每个小段的场可以通过安培环路定律来计算，该定律描述了通过电流所产生的磁场。通过将每个小段的贡献相加，我们可以得到整个导线在某一点的总磁场大小和方向。这种方法允许我们在三维空间中准确地建模复杂形状的导线，并预测在任何给定点的磁场强度和方向。一旦得到了这些数据，我们可以使用箭头图来可视化磁场的矢量流动。箭头的长度和方向表示磁场的强度和方向，从而使观察者能够直观地理解磁场的分布情况。这种可视化方法对于理解导线周围的磁场分布以及预测磁场对周围物体的影响具有重要意义。

一、毕奥-萨伐尔定律的数学表达式

毕奥-萨伐尔定律是计算电流元产生磁场的基础。其核心公式描述为：

其中：

dB为电流元 I dlIdl 在观察点产生的磁感应强度；
μ0=4π×10−7 T⋅m/AT⋅m/A 为真空磁导率；
dl为电流元矢量，方向与电流方向一致；
r^为从电流元指向观察点的单位矢量；
r为电流元到观察点的距离。
磁场方向由右手定则确定，垂直于 dldl 和 r^r^ 构成的平面。

二、有限长度直导线的磁场积分推导

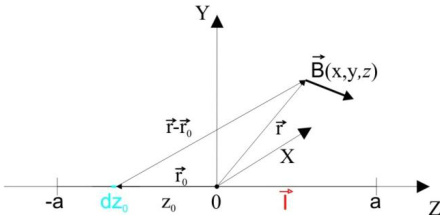
对于有限长度直导线，需对电流元的磁场贡献沿导线积分。设导线沿 zz 轴从 z1z1 到 z2z2，观察点坐标为 (x,y,z)(x,y,z)，具体步骤如下：

（注：直导线的磁场无轴向分量，仅存在于垂直平面内）。
积分求解：

通过变量替换（如 u=z′−z）可解析积分，结果与角度和距离相关。

三、数值计算方法与离散化处理

对于复杂几何或三维磁场分布，需采用数值积分方法：

导线离散化：将导线分为 N 小段，每段长度 Δl，电流元近似为 IΔl。
磁场叠加：计算每段电流元在观察点的磁场，矢量叠加总磁场：

四、三维磁场矢量叠加原理

磁场叠加需遵循矢量加法规则：

分量分解：将各电流元的磁场分解至 x,y,z 轴，如：
对称性简化：
- 直导线的磁场关于导线轴对称，可采用圆柱坐标系 (ρ,ϕ,z)，仅保留 Bϕ分量；
- 在导线中点垂面内，磁场仅有环向分量，且强度随 ρ−1衰减。
可视化示例：
- 在导线两侧，磁场线呈同心圆分布；
- 导线端点附近磁场方向复杂，存在径向分量（图2, ）。

五、与安培环路定律的对比及适用性

无限长导线：安培定律简化为 B=μ0I2πρ，与毕奥-萨伐尔积分结果一致。
有限长导线：
- 安培定律失效：因磁场旋度 ∇×B 不连续，无法满足静磁条件；
- 必须使用毕奥-萨伐尔定律：直接积分计算全空间磁场分布。
物理意义：有限长导线的电流两端电荷积累导致电场变化，需引入位移电流修正（安培-麦克斯韦方程），但磁场计算仍依赖毕奥-萨伐尔定律。

六、应用案例与文献分析

亥姆霍兹线圈：
- 由两平行同轴圆环电流组成，磁场均匀性通过叠加原理优化；
- 类似方法可推广至有限长直导线的阵列设计。
电磁兼容性分析：
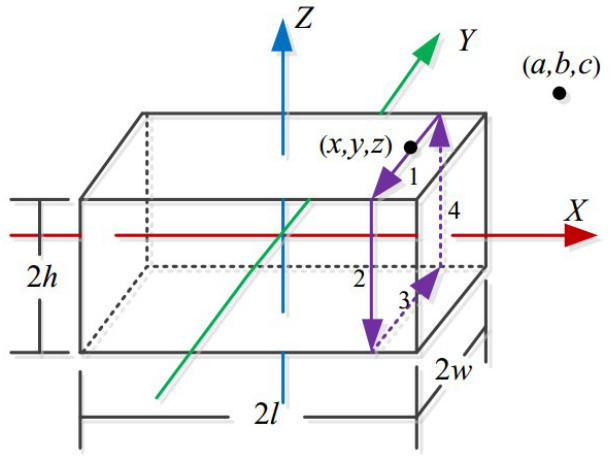
- 计算PCB走线或电力母线的磁场辐射（图6, ）；
- 离散化方法提升计算效率（对比点偶极子模型，误差约5%）。
医学成像与磁控机器人：
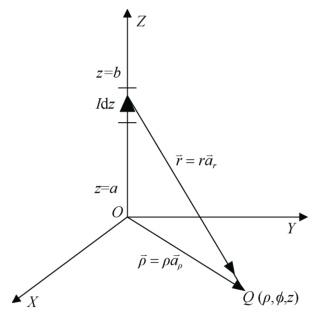
- RectMag3D系统利用矩形线圈和毕奥-萨伐尔定律实现三维磁操控（图3, ）。

七、总结与拓展

核心方法：离散化积分 + 矢量叠加是有限长导线磁场计算的标准流程；
进阶方向：
- 结合快速多极子算法（FMM）提升大规模计算效率；
- 时变电流下的磁场计算需引入推迟势（Jefimenko方程）。
实验验证：通过霍尔探头测量磁场分布，对比数值结果（如DH4501N实验仪）。

通过上述分析，毕奥-萨伐尔定律不仅是理论工具，更是工程实践中磁场建模的核心方法，其应用从基础物理教学延伸至现代电磁设备设计。

📚2 运行结果

一个有限的导线被分成许多小段，每个段的场被求和，以获得导线在3D空间中的总磁场。最后，显示箭头图以可视化矢量流动。

部分代码：

line([-5 5],[0 0], [0 0],'linewidth',3,'color','r');
axis([-5 5 -5 5 -5 5])
xlabel('X-axis','fontsize',14)
ylabel('Y-axis','fontsize',14)
zlabel('Z-axis','fontsize',14)
title('B-field of a current wire along X-axis','fontsize',14)
h=gca;
set(h,'FontSize',14)
fh = figure(1);
set(fh, 'color', 'white');

figure(2)

quiver(Y((Nx-1)/2,:,:),Z((Nx-1)/2,:,:),BY((Nx-1)/2,:,:),BZ((Nx-1)/2,:,:),2);
hold on
G1=plot(0,0,'.','markersize',6);
set(G1,'MarkerEdgeColor','r')
axis([ -5 5 -5 5])
xlabel('Y-axis','fontsize',14)
ylabel('Z-axis','fontsize',14)
title('B-field YZ plane','fontsize',14)
h=gca;
set(h,'FontSize',14)
h = get(gca, 'ylabel');
fh = figure(2);
set(fh, 'color', 'white');
%--------------------------------------------------------------------------