用于永磁同步电机驱动器的自适应SDRE非线性无传感器速度控制（Matlab&Simulink实现）-CSDN博客

本文链接：https://blog.csdn.net/weixin_46039719/article/details/148035329

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、引言

二、研究背景与意义

三、研究方法

四、研究结果与分析

五、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码&Simulink仿真实现

💥1 概述

本文方法基于状态依赖的里卡蒂方程（SDRE）控制技术及其梯度型神经网络的实时计算方法，允许在线控制PMSM。

为了实现用于永磁同步电机驱动器的自适应 SDRE（State-Dependent Riccati Equation）非线性无传感器速度控制，按照以下步骤进行。

1. 确定系统的动态模型：首先，获得永磁同步电机的动态模型。该模型通常由磁链方程、电流方程和机械方程等组成。根据电机的具体参数和特性，推导出系统的状态空间表达式。

2. 设计自适应 SDRE 控制器：基于系统的状态空间表达式，采用自适应 SDRE 控制策略进行设计。自适应 SDRE 控制是一种基于 Riccati 方程调节器的非线性控制方法，它通过自适应参数来优化控制器的性能。具体设计步骤包括：设置控制器结构、定义控制误差目标和性能指标、计算状态反馈增益矩阵和 Riccati 方程解。

3. 实现无传感器速度估计器：由于无传感器速度控制，需要通过估计器来获取电机转速的信息。可以采用滑模观测器或者其他速度估计器来实现，以获得无传感器的速度测量。

4. 连接控制器和估计器：将自适应 SDRE 控制器和无传感器速度估计器与电机的动态模型相连接。确保控制器能够接收估计到的速度信号，并提供相应的控制输出。

5. 仿真和调试：在 Simulink 环境中建立仿真模型，并进行仿真验证。通过逐步参数调整和性能评估，对控制系统进行调试和优化。

用于永磁同步电机驱动器的自适应SDRE非线性无传感器速度控制研究

一、引言

永磁同步电机（PMSM）因其高效率、高功率密度和良好的动态性能，在电动汽车、工业驱动和风力发电等领域得到了广泛应用。然而，传统的PMSM速度控制方法依赖于速度传感器来获取转速信息，这不仅增加了系统的复杂性和成本，还降低了系统的鲁棒性和可靠性。因此，研究无传感器的速度控制方法对于PMSM驱动器的发展具有重要意义。本文基于自适应系统动态逆控制（SDRE）技术，探讨了一种非线性无传感器速度控制方法，旨在减少对传感器的依赖并提高系统的性能。

二、研究背景与意义

传感器依赖性问题：传统PMSM速度控制方法中，速度传感器是关键部件，但其存在成本高、易故障、易受环境干扰等问题，影响系统的整体性能。
系统鲁棒性提升：无传感器速度控制方法能够克服传感器带来的限制，提高系统的鲁棒性和可靠性，降低维护成本。
自适应SDRE技术的优势：SDRE是一种非线性控制方法，能够适应系统的非线性特性，并且不需要精确的系统模型。基于SDRE的无传感器速度控制方法，结合自适应控制策略，能够实现高性能的速度控制。

三、研究方法

数学模型建立
- 建立PMSM的数学模型，包括电压方程、磁链方程和转矩方程等，为后续控制算法的设计提供基础。
自适应SDRE控制策略
- 采用SDRE控制策略，根据系统的实时状态动态调整控制参数，实现对PMSM驱动器的高性能速度控制。
- 利用梯度型神经网络的实时计算方法，实现控制参数的在线优化，提高系统的适应性和鲁棒性。
无传感器速度估计
- 结合电机的非线性特性和自适应控制策略，通过电机电流、电压等可测量信号，实时估计电机的转速信息。
- 利用观测器或滤波器等技术手段，提高速度估计的精度和稳定性。
仿真与实验验证
- 在Matlab/Simulink环境下搭建PMSM驱动器的仿真模型，对提出的控制算法进行仿真验证。
- 设计实验平台，对实际PMSM驱动器进行测试，验证控制算法的有效性和优越性。

四、研究结果与分析

仿真结果
- 仿真结果表明，基于自适应SDRE的非线性无传感器速度控制方法能够准确估计电机的转速信息，实现高精度的速度控制。
- 在不同负载和工况下，系统均表现出良好的动态响应和稳定性。
实验结果
- 实验结果进一步验证了仿真结果的正确性。在实际PMSM驱动器上，该控制方法能够有效实现无传感器速度控制，降低系统对传感器的依赖。
- 与传统控制方法相比，该方法在控制精度、鲁棒性和动态响应等方面均表现出明显的优势。

五、结论与展望

结论
- 本文基于自适应SDRE技术，提出了一种用于PMSM驱动器的非线性无传感器速度控制方法。通过仿真和实验验证，该方法能够准确估计电机转速信息，实现高性能的速度控制，并且具有较强的鲁棒性和适应性。
展望
- 未来研究可以进一步优化控制算法，提高速度估计的精度和稳定性。
- 探索更多先进的控制策略和技术手段，如深度学习、人工智能等，以进一步提升PMSM驱动器的性能和智能化水平。

通过本文的研究，为PMSM驱动器的无传感器速度控制提供了一种新的思路和方法，为工业应用和科研领域提供了更加可靠和高效的控制方案。

📚2 运行结果

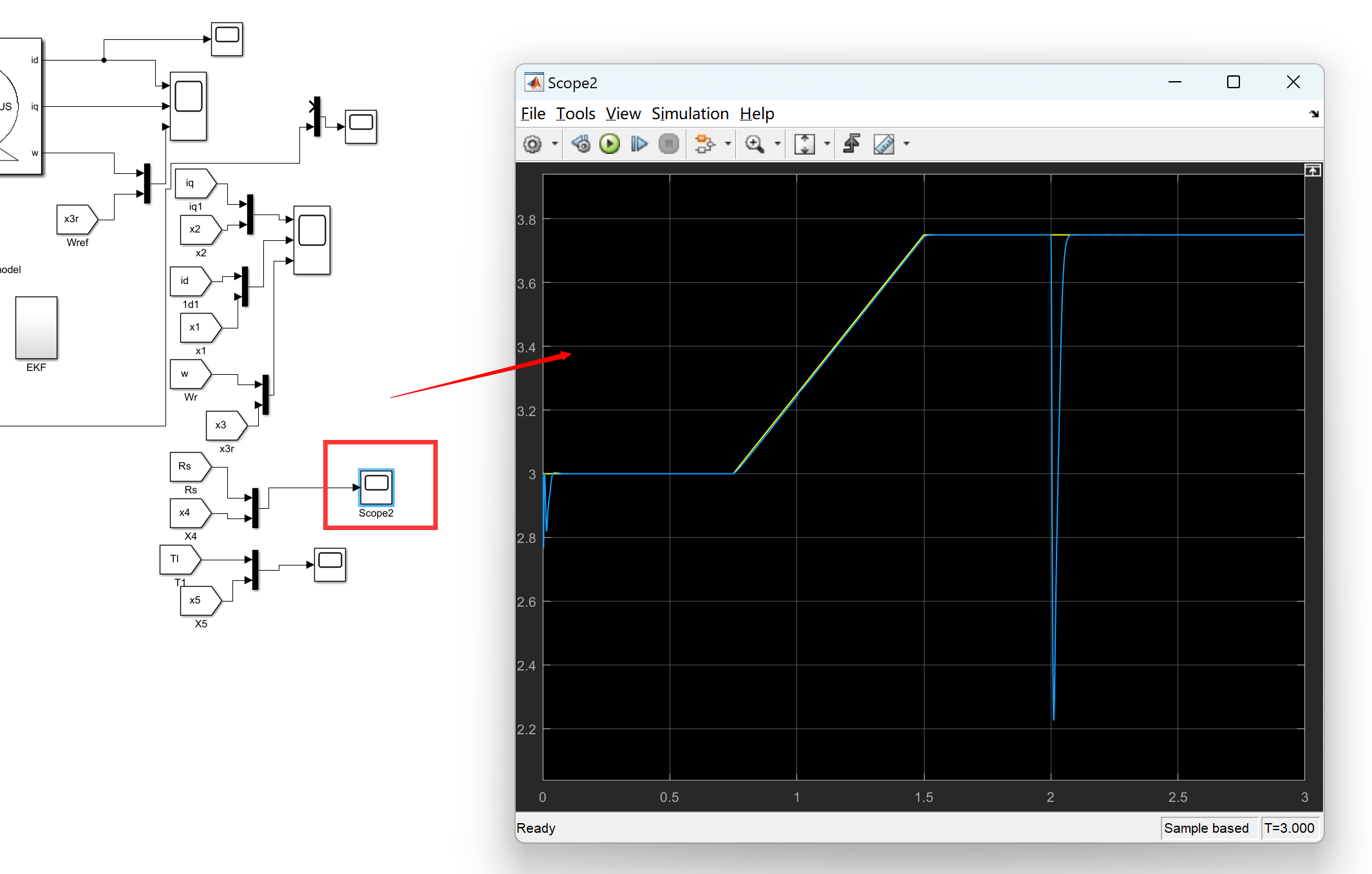
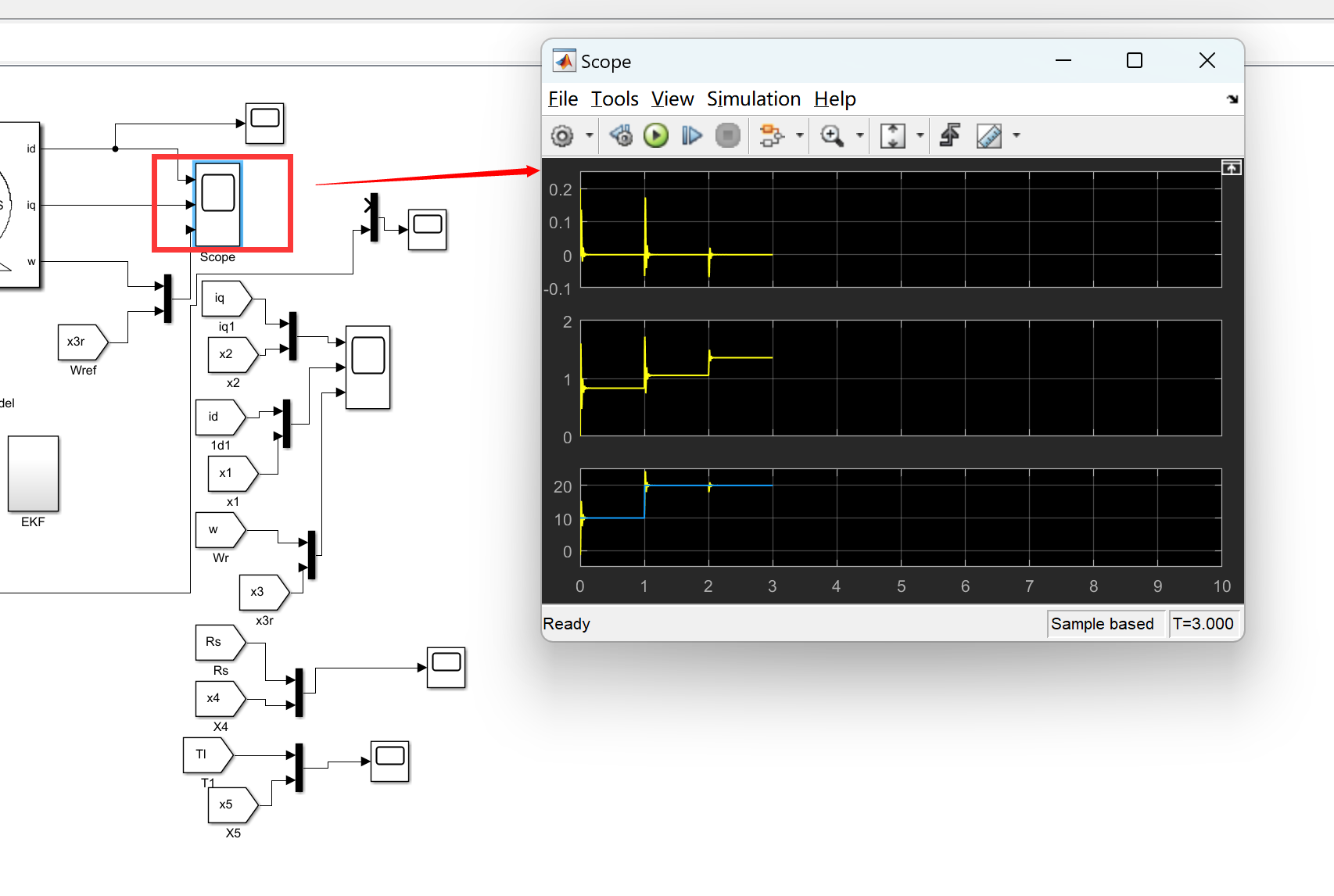
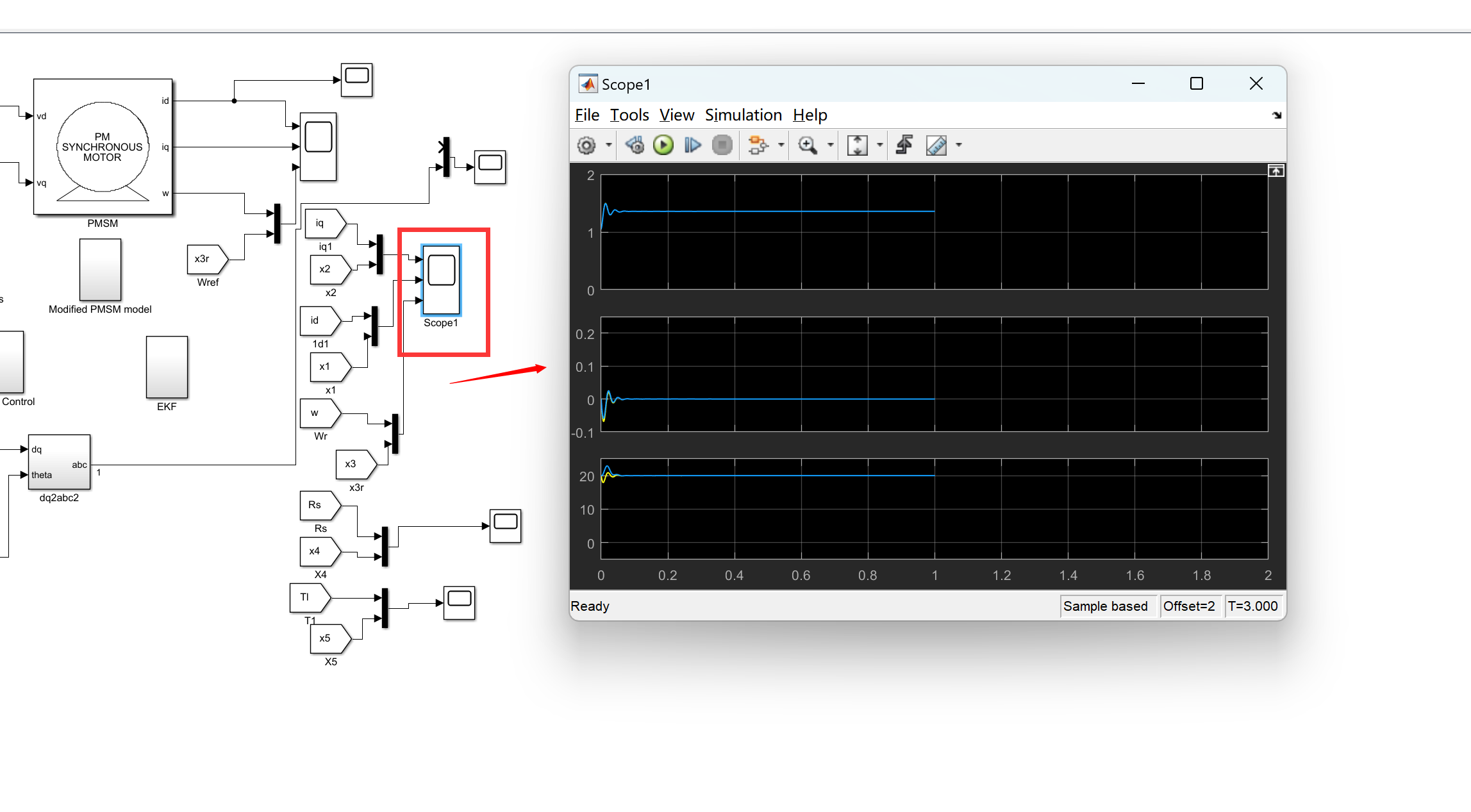matlab程序：

clc
clear all

Rs=0.625
Ld=0.036
Lq=0.051
phi=0.545
J=7.5e-4
F=0.036
P=2
% a1=R/Ld
a2=P*Lq/Ld
a3=P*Ld/Lq
% a4=R/Lq
a5=P*phi/Lq
a6=3/2*P*phi/J
a7=F/J
B=[1 0;0 1;0 0]

Qc=[1 0 0;0 1 0;0 0 1]
R=[1 0;0 10]
x2dot=0
x3dot=0
gama=0.1
% syms a1 a2 a3 a4 a5 a6 a7 x1 x2 x3 R
% f=[-a1*R*x1+a2*x2*x3; -a3*x1*x3-a4*R*x2-a5*x3; a6*x2-a7*x3-1/J*Tl;0]
% jacobian(f,[x1 x2 x3 R ])
% E=4300170000*[1e-6 0 0 0 ;0 1e-6 0 0 ;0 0 1e-6 0 ;0 0 0 1e-6 ]
Rk=0.09*[1 0;0 1]
E=4300180000*[1e-6 0 0 0 0 ;0 1e-6 0 0 0 ;0 0 1e-6 0 0 ;0 0 0 1e-2 0; 0 0 0 0 1e-5]