【9种优化算法比较】CGO、SCA、GWO、CSA、SSA、HHO、WOA、PSO、TSO智能优化算法比较（Matlab代码实现）

荔枝科研社

于 2025-05-19 10:34:52 发布

阅读量617

点赞数 22

文章标签：算法 matlab 数学建模

本文链接：https://blog.csdn.net/weixin_46039719/article/details/148057977

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、算法核心思想与数学模型对比

二、优缺点总结

三、典型应用场景

四、性能指标对比

五、异同点分析

六、总结

📚2 运行结果

2.1 F1

2.2 F2

2.3 F3

2.4 F7

2.5 部分代码

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

先看看效果，比比谁更好：

以下是对9种智能优化算法（CGO、SCA、GWO、CSA、SSA、HHO、WOA、PSO、TSO）的比较研究文档，涵盖核心思想、优缺点、应用场景、性能指标和异同点分析：

一、算法核心思想与数学模型对比

算法	核心思想	数学模型特点
CGO	基于混沌理论的分形自相似性，利用Sierpinski三角形生成新个体增强全局搜索	四种种子位置更新公式，结合混沌随机矩阵和最优解动态调整
SCA	通过正弦/余弦函数的周期性振荡平衡全局搜索与局部开发	位置更新公式中线性递减参数r1控制探索-开发转换
GWO	模仿灰狼社会等级（α/β/δ/ω）的狩猎策略	基于α、β、δ的位置加权更新个体位置
CSA	类搜索模型结合差分进化，调节簇类结构优化搜索机制	层次聚类构造类组织，融合DE的变异策略
SSA	模拟麻雀觅食与反捕食行为，分发现者、跟随者、警戒者角色	发现者随机探索，跟随者追踪最优，警戒者逃离危险
HHO	模仿哈里斯鹰的协同捕猎策略（软/硬包围、俯冲攻击）	动态逃逸能量参数控制四种狩猎模式切换
WOA	鲸鱼气泡网攻击行为的数学建模（包围、螺旋更新、随机搜索）	参数a控制搜索半径，螺旋方程模拟收缩包围
PSO	粒子群协作共享个体与群体最优经验	速度更新公式含惯性权重、个体/社会学习因子
TSO	模拟电路瞬态振荡行为，平衡探索与开发	热阻系数和衰减系数调节搜索步长

二、优缺点总结

算法	优点	缺点
CGO	全局搜索能力强，分形结构增强多样性	计算成本较高，参数调整复杂
SCA	结构简单、参数少，适用于高维问题	线性递减策略易导致前期收敛过快
GWO	收敛速度快，社会等级模型简单有效	高维问题易陷入局部最优
CSA	类结构动态调节，稳定性高	实现复杂度较高，依赖聚类质量
SSA	收敛快、鲁棒性强，适应多模态问题	种群多样性后期下降，需改进初始策略
HHO	多种捕猎策略灵活切换，局部搜索能力强	参数敏感，逃逸能量调节需优化
WOA	全局搜索性能优异，适用于非线性问题	局部开发不足，初始种群依赖性高
PSO	实现简单，快速收敛，易于并行化	易早熟收敛，后期搜索效率低
TSO	物理模型直观，平衡探索与开发	应用场景有限，需更多工程验证

三、典型应用场景

算法	应用领域	具体案例
CGO	路径规划、工程优化	复杂动态环境下的机器人路径生成
SCA	电力调度、参数优化	SVM核函数参数选择、微电网能量管理
GWO	能源系统、结构设计	风-光-储协同优化、航空发动机轮盘设计
CSA	高维优化、数据聚类	WSN覆盖优化、医学数据特征选择
SSA	机器学习、环境监测	土壤供肥量预测、水质评价
HHO	图像处理、故障诊断	医疗影像分割、风力发电机故障检测
WOA	医学影像、计算机视觉	图像分类、光伏模型参数提取
PSO	控制工程、神经网络	PID控制器调参、CNN-GRU网络优化
TSO	电力系统参数整定	分布式光伏-VSG功频参数优化

四、性能指标对比

指标	CGO	SCA	GWO	CSA	SSA	HHO	WOA	PSO	TSO
收敛速度	中	快	快	慢	快	中	中	快	中
全局搜索	强	较强	一般	较强	强	较强	强	一般	较强
鲁棒性	高	高	中	高	高	中	中	低	中
局部开发	一般	强	强	中	较强	强	较弱	强	中

数据来源：

五、异同点分析

设计思想：
- 仿生类：GWO（狼群）、SSA（麻雀）、HHO（鹰）、WOA（鲸鱼）均模拟生物行为；物理模型类：TSO（电路瞬态）、CGO（混沌分形）。
- 数学驱动类：SCA（三角函数）、PSO（群体协作）、CSA（类结构聚类）。
探索-开发平衡机制：
- 动态参数：SCA（r1线性递减）、HHO（逃逸能量）、WOA（参数a）。
- 多策略切换：CGO（四种种子更新）、HHO（四种捕猎模式）。
适用问题类型：
- 高维复杂问题：CGO、CSA、SSA表现更优。
- 实时性要求高：PSO、GWO、SCA因收敛快更适用。

六、总结

CGO和SSA在全局搜索和鲁棒性上表现突出，适合复杂优化问题；SCA和PSO因结构简单广泛用于工程参数调优；HHO和GWO在局部开发能力上有优势；TSO和CSA作为新兴算法，需更多应用验证。未来趋势包括混合算法（如CGGWO）和多策略改进，以平衡性能与计算成本。

📚2 运行结果

2.1 F1

2.2 F2

2.3 F3

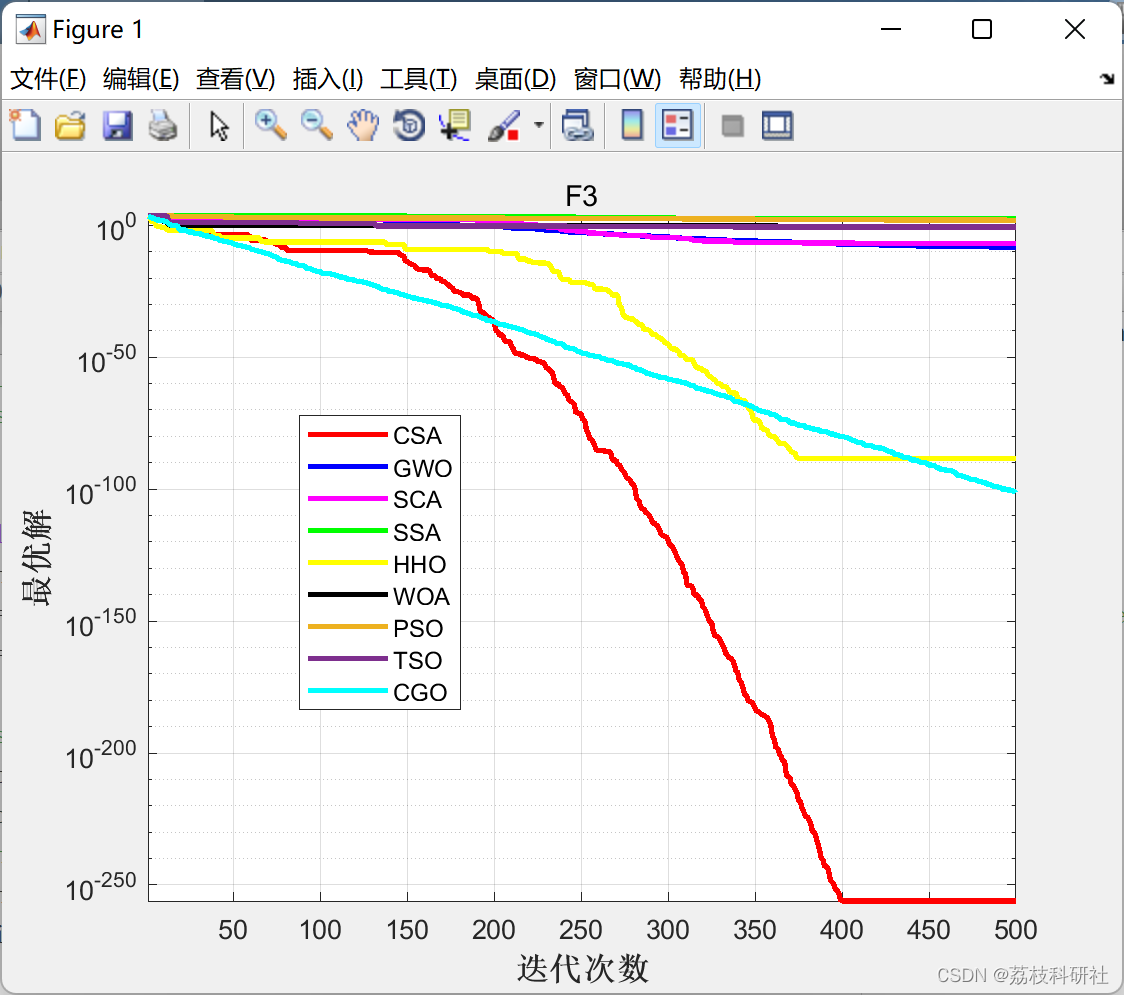
就不一一例举啦，直接到F7：

2.4 F7

2.5 部分代码

semilogy(curve8,'Color','b','LineWidth',2)%GWO
semilogy(curve2,'Color','m','LineWidth',2)%SCA
semilogy(curve3,'Color','g','LineWidth',2)%SSA
semilogy(curve4,'Color','y','LineWidth',2)%HHO
semilogy(curve5,'Color','k','LineWidth',2)%WOA
semilogy(curve6,'Color',[0.9290 0.6940 0.1250],'LineWidth',2)%PSO
semilogy(curve7,'Color',[0.4940 0.1840 0.5560],'LineWidth',2)%TSO
semilogy(curve9,'Color','c','LineWidth',2)%CGO
title(Function_name)
xlabel('迭代次数','fontsize',12,'FontWeight','bold');
ylabel('最优解','fontsize',12,'FontWeight','bold');
axis tight
grid on
box on
legend('CSA','GWO','SCA','SSA','HHO','WOA','PSO','TSO','CGO') %,'fontsize',12,'FontWeight','bold','FontName','Arial Narrow'

disp(["CSA"," SCA"," SSA"," HHO"," WOA"," PSO"," TSO"," GWO"," CGO"])
output=[X_c1 X_c2 X_c3 X_c4 X_c5 X_c6 X_c7 X_c8 X_c9]

以下是23个测试函数：

function [lb,ub,dim,fobj] = Get_Functions_details(F)
dim1=30;

switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=dim1;

case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=dim1;

case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=dim1;
case 'F33'
fobj = @F33;
lb=-10;
ub=10;
dim=dim1;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=dim1;

case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=dim1;

case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=dim1;

case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=dim1;

case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=dim1;
case 'F88'
fobj = @F88;
lb=-0.5;
ub=0.5;
dim=dim1;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=dim1;
case 'F100'
fobj = @F100;
lb=-5.12;
ub=5.12;
dim=dim1;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=dim1;

case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=dim1;

case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=dim1;

case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=dim1;

case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;

case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;

case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;

case 'F17'
fobj = @F17;
lb=-5;
ub=5;
dim=2;

case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;

case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;

case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;

case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;

case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;

case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end

end

% F1

function o = F1(x)
o=sum(x.^2); %sphere
end

% F2

function o = F2(x)
o=sum(abs(x))+prod(abs(x)); %shwefel 2.22
end

% F3

function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2; %Schwefel 1.2
end
end
function o = F33(x)
dim=size(x,2);

o=sum(([1:dim].*x).^2); %sum squares
end
% F4

function o = F4(x)
o=max(abs(x)); %Schwefel 2.21
end

% F5

function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2); %Rosenbrock
end

% F6

function o = F6(x)
o=sum(abs((x+.5)).^2); %step
end

% F7

function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand; %Quartic Noise
end

% F8

function o = F8(x)
dim=size(x,2);
o=sum(-x.*sin(sqrt(abs(x)))); %Schwefel 2.26 +418.9829*dim
end

% F9
function o = F88(x) %Weierstrass
dim=size(x,2);a=0.5;b=3;kmax=21;o=0;
for i=1:dim
for j=1:kmax
o=o+a*cos(2*pi*b*(x(1,i)+0.5));
end
end
for n=1:kmax
o=o-dim*a*cos(2*pi*b*0.5);
end

end

function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim; %Rastrigin
end

function o = F100(x) % Non continous Rastrigin
dim=size(x,2);y=zeros(1,dim);
for i=1:dim
if (x(1,i)>=0.5 || x(1,i)<=-0.5)
y(1,i)=round(2*x(1,i))/2.0;
else
y(1,i)=x(1,i);
end

end
o=sum(y.^2-10*cos(2*pi.*y))+10*dim;
end
% F10

function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1); %Ackley
end

% F11

function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1; %Griewank
end

% F12

function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4)); %Pendlized
end

% F13

function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4)); %Generalized Pendlized

end

% F14

function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];

for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end

% F15

function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end

% F16

function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end

% F17

function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end

% F18

function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2))); %Goldstein Price
end

% F19

function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F20

function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F21

function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F22

function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F23

function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end