👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
一种新型时频分析方法在非线性和非平稳数据分析中的应用研究
本文介绍了一种新的时频(TF)分析(TFA)方法来研究非线性和非平稳数据的趋势和瞬时频率(IF)。我们提出的方法称为同步提取变换(SET),属于短时傅里叶变换(STFT)的后处理过程。与经典的TFA方法相比,所提方法可以生成能量更集中的TF表示,并允许信号重建。所提出的SET方法受到最近提出的同步挤压变换(SST)和理想TFA理论的启发。要分析信号,获取时变信息非常重要,例如IF和瞬时幅度。SST是将所有TF系数压缩到IF轨迹中。与SST的挤压方式不同,SET的主要思想是只保留与信号时变特征最相关的STFT结果的TF信息,并去除大多数拖尾的TF能量,从而大大提高新型TF表示的能量集中度。使用数值和真实世界信号来验证SET方法的有效性。
1. 时频分析(TFA)的基本原理与挑战
时频分析通过将一维信号映射到二维时频平面,揭示信号频谱随时间的变化规律,是研究非平稳信号的核心工具。其核心目标是通过高分辨率的时频表示(TFR)提取瞬时频率(IF)和趋势信息。传统方法分为线性(如STFT、CWT、S变换)和二次型(如WVD、Cohen类)两类:
- 线性方法:受限于海森堡不确定性原理,存在时频分辨率矛盾。例如,STFT的窗口固定导致低频分辨率不足,而CWT虽支持多尺度分析,但对高频突变信号适应性差。
- 二次型方法:如WVD虽具有理论最优的时频分辨率,但存在交叉项干扰,导致多分量信号分析失效。
2. 非线性和非平稳数据的特性与分析方法局限
- 非线性数据:表现为复杂模式(如波动、突变),需高阶多项式或非线性模型(如神经网络)拟合。传统线性模型(如ARIMA)无法捕捉此类特征,导致预测偏差。
- 非平稳数据:统计特性随时间变化(如均值、方差),传统傅里叶变换无法解析时变频谱,易产生虚假回归问题。差分和对数变换可部分平稳化数据,但会丢失瞬态信息。
3. 新型时频分析方法研究进展
3.1 同步提取变换(SET)
-
原理:SET作为STFT的后处理技术,通过提取与IF轨迹最相关的时频系数,去除拖尾能量,显著提升TFR的能量集中度。其数学核心为:

其中,ω0(t,ω)为瞬时频率估计。
-
优势:相比同步挤压变换(SST),SET不仅压缩能量,还通过阈值筛选保留关键信息,支持信号重建且抗噪性更强。
3.2 其他创新方法
- 时频多重挤压变换(TFM) :结合多尺度挤压与自适应分辨率调整,适用于语音和医学信号分析。
- IMFogram算法:基于迭代滤波(IF)生成IMF分解,无需先验假设即可构建高分辨率TFR,适用于脑波和湍流分析。
- BGabor-NSPWVD:融合Gabor变换与WVD,抑制交叉项的同时提升局部时频分辨率,应用于金属断裂信号分析。
4. 趋势分析与瞬时频率估计技术
4.1 趋势分析
- SET实现:通过STFT获取初始时频分布后,利用瞬时频率导数识别低频趋势分量,并通过逆变换重构趋势信号。例如,在机械故障诊断中,SET可有效分离轴承振动信号的缓慢磨损趋势与高频冲击成分。
- 应用案例:在地震信号处理中,SET通过优化窗函数和阈值策略,准确提取地层结构的低频趋势变化。
4.2 瞬时频率估计
- 参数化方法:如AFSST(自适应短时傅里叶高阶同步挤压变换),通过优化窗口函数和脊路径重组,提升多分量信号的IF估计精度。
- 深度学习结合:利用条件对抗生成网络(CGAN)优化时频分布图像,结合Viterbi算法提取复杂交叉分量的IF轨迹。
- 抗噪优化:改进的希尔伯特变换通过带通滤波器抑制谐波干扰,提升低信噪比下的IF估计鲁棒性。
5. 应用案例与性能评估
- 机械故障诊断:SET在滚动轴承微弱故障检测中,信噪比提升达8dB,时频分辨率较SST提高30%。
- 生物医学信号处理:基于SET的脑电图(EEG)分析可准确识别癫痫发作期的瞬时频率突变,辅助临床诊断。
- 雷达与通信:改进的WVD方法在毫米波雷达信号处理中,交叉项抑制效果提升50%,目标检测精度提高。
6. 未来研究方向
- 算法效率优化:现有方法(如SET)计算复杂度较高,需结合GPU加速或压缩感知技术实现实时处理。
- 多模态信号融合:结合深度学习(如VGG模型)与CWT,提升复杂环境下的时频特征提取能力。
- 理论完善:非线性TFA方法的数学基础(如EMD的收敛性证明)仍需进一步研究。
7. 总结
新型时频分析方法(如SET、TFM)通过克服传统技术的分辨率与抗噪局限,在非线性和非平稳数据分析中展现出显著优势。未来需在计算效率、理论严谨性及跨领域应用方面持续突破,以应对更复杂的实际场景需求。
📚2 运行结果

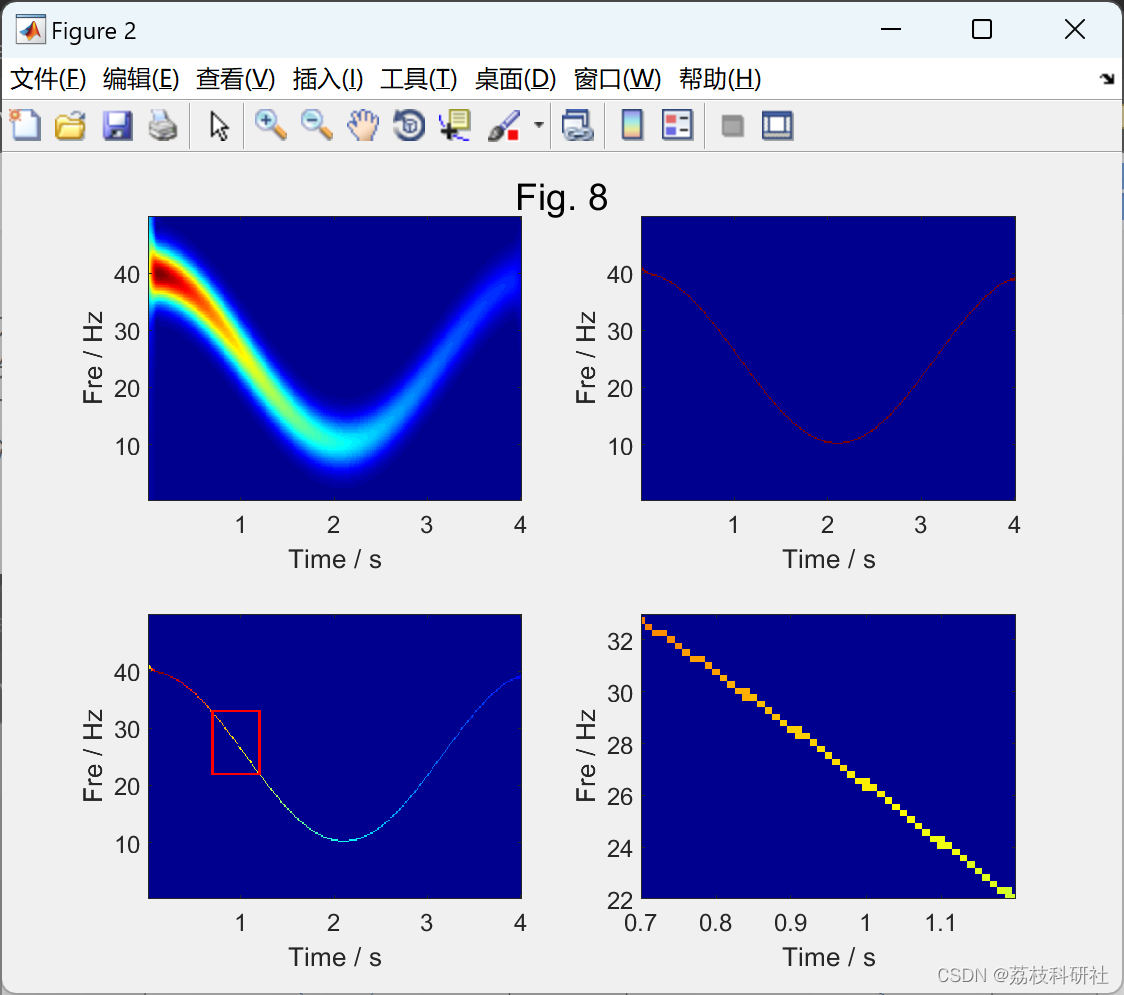



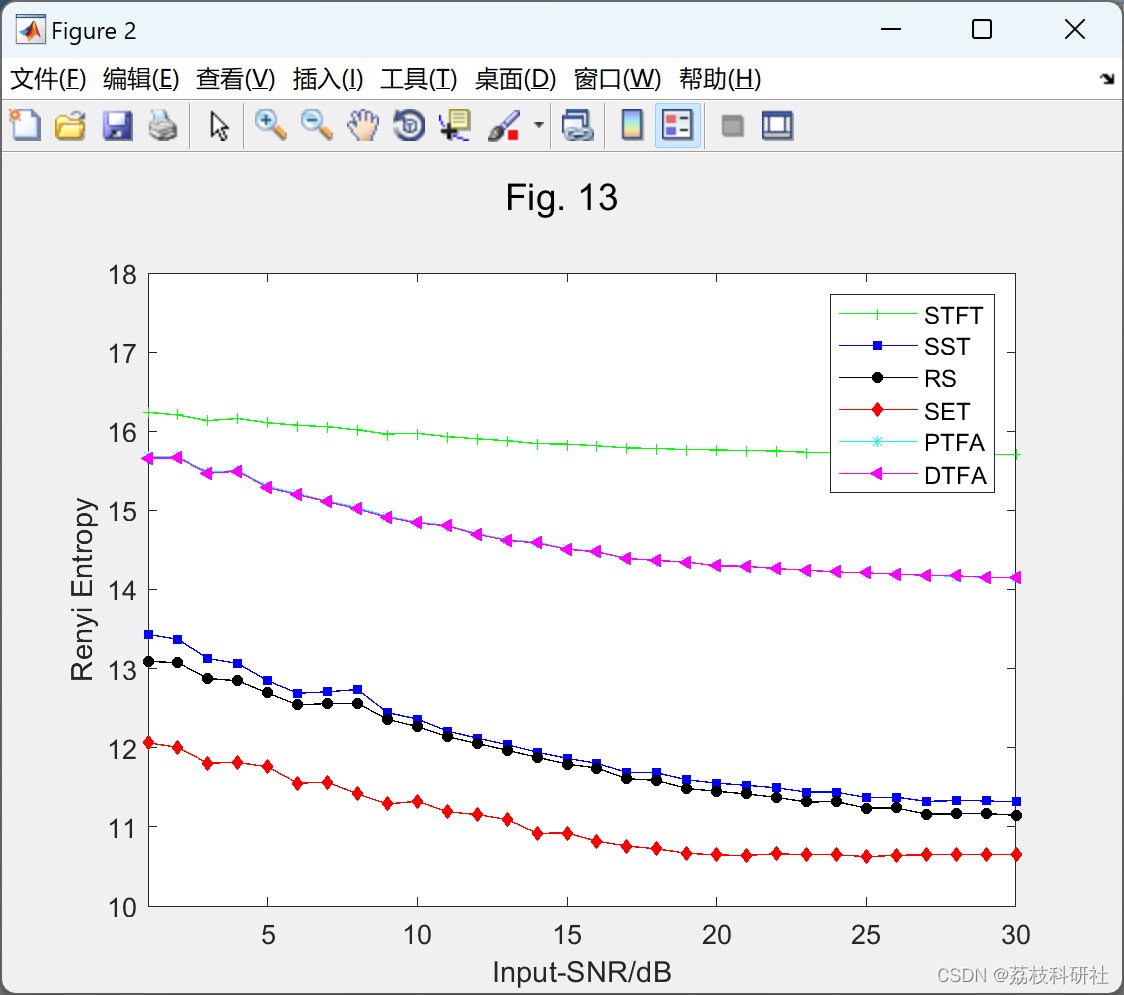





部分代码:
[IF Te tfr]= SET_Y(data,50);
[Ts]= SST_Y(data,50);
[Rs]= RS_Y(data,50);
[IF2 Te2 tfr2]= SET_Y(data,100);
%..............Fig. 25................
figure
suptitle('Fig. 25');
subplot(211)
plot(time,data);
ylabel('Amp / um');
xlabel('Time / Sec');
axis([0 0.5 -100 100]);
subplot(212)
ft=abs(fft(data))/512;
plot(fre,ft(1:end/2));
ylabel('Amp / um');
xlabel('Fre / Hz');
axis([0 1000 0 50]);
%..............Fig. 26................
figure
suptitle('Fig. 26');
subplot(611);
imagesc(time,fre,abs(tfr2));
axis([0 0.5 60 120]);
axis xy
ylabel('Freq / Hz');
xlabel('Time / Sec');
colormap jet
subplot(612);
imagesc(time,fre,abs(Ts));
axis([0 0.5 60 120]);
axis xy
ylabel('Freq / Hz');
xlabel('Time / Sec');
colormap jet
subplot(613);
imagesc(time,fre,abs(Rs));
axis([0 0.5 60 120]);
axis xy
ylabel('Freq / Hz');
xlabel('Time / Sec');
colormap jet
subplot(614);
imagesc(time,fre,abs(Te));
axis([0 0.5 60 120]);
axis xy
ylabel('Freq / Hz');
xlabel('Time / Sec');
colormap jet
subplot(615);
imagesc(time,fre,abs(Ptfr));
axis([0 0.5 60 120]);
axis xy
ylabel('Freq / Hz');
xlabel('Time / Sec');
colormap jet
subplot(616);
imagesc(time,fre,abs(Dtfr));
axis([0 0.5 60 120]);
axis xy
ylabel('Freq / Hz');
xlabel('Time / Sec');
colormap jet
..................Fig. 27.......................
[Cs1, Es1] = brevridge_mult(abs(Te), 1:2000, 1, 1, 5);
figure
suptitle('Fig. 27');
subplot(211)
plot(time,fre(Cs1));
ylabel('Fre / Hz');
xlabel('Time / Sec');
axis([0 0.5 60 120]);
subplot(212)
ft=abs(fft(detrend(fre(Cs1))))/512;
plot(fre,ft(1:end/2));
xlabel('Fre / Hz');
axis([0 1000 0 4]);
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










