1、图卷积神经网络(GCN)定义
图卷积神经网络(Graph Convolutional Networks,GCN)是一种专门用于处理图形数据的神经网络架构。图形数据指的是由节点V(vertices)和边E(edges)组成的图形结构,常见于社交网络、分子结构、交通网络等领域。GCN 的核心在于能够直接在图结构上运行,捕捉节点之间的复杂关系和结构特征。
2、图卷积神经网络的发展历程
- 早期探索阶段(约2009年前后):
- 这个时期的研究主要集中在如何将传统的神经网络方法应用到图数据上。早期的图神经网络(GNN)模型往往计算成本高,且难以扩展到大型图。
- 谱方法的引入(约2013-2016年):
- 研究者开始探索基于图的谱理论来定义图卷积。这一方法基于图的拉普拉斯矩阵,通过谱分解来理解图卷积。
- 代表性的工作包括Bruna等人在2013年的论文,他们提出了基于谱理论的图卷积网络。
- 空间方法的发展(约2016年至今):
- 2016年左右,研究者开始转向空间方法,这种方法直接在图的节点上应用卷积,而不是通过谱分解。
- Kipf和Welling在2016年提出了一种简化的图卷积网络模型(GCN),大大降低了计算复杂性,并在多个任务上表现出色,成为了图卷积网络研究的里程碑。
- 最新发展:
- 近年来,图神经网络的研究迅速发展,涌现出多种变体和改进,如图注意力网络(GAT)、图变换网络(GTN)等。
- 研究者也在探索将图卷积网络应用于更广泛的领域,如推荐系统、药物发现、自然语言处理等。
GCN 的发展代表了深度学习领域对非欧几里得数据处理能力的显著提升,同时也展示了深度学习在多样化数据类型上的广泛适用性。随着算法和计算能力的不断进步,GCN 及其相关变体在未来可能会有更多的创新和应用。
3、从CNN说起
tag:这里出一篇卷积神经网络
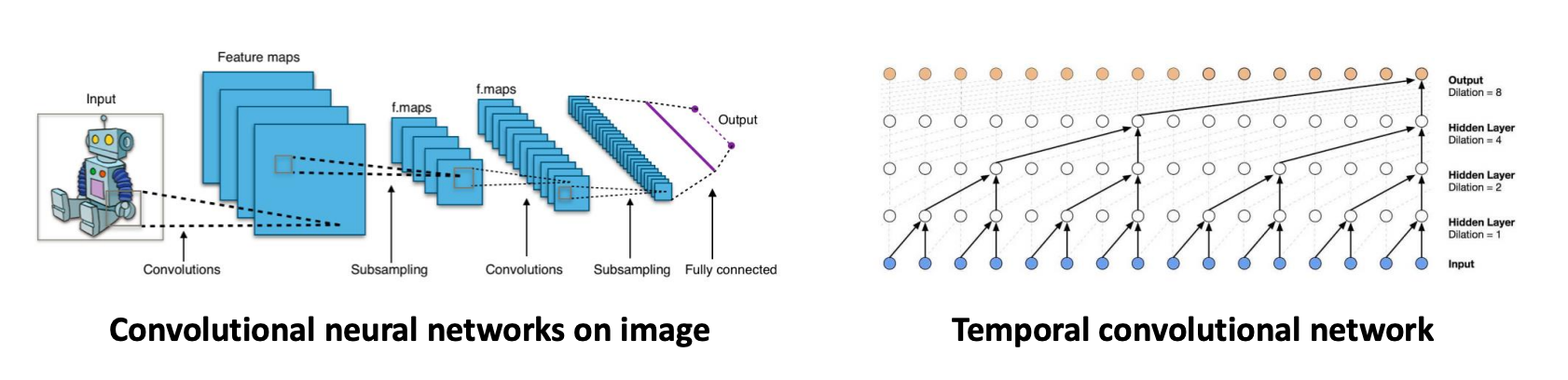
这张图说明了卷积神经网络(CNN)和它们在处理欧几里得数据(如图像、文本、音频和视频)方面的应用。CNN在图像分类、对象检测和机器翻译等领域应用广泛。
值得一提的是,CNN在处理欧几里得数据方面是非常成功的!
左边的部分展示了CNN在图像上的应用,描述了一个典型的CNN架构,包括卷积层、子采样层(也称为池化层)、再次卷积和子采样,最后是全连接层,这是进行分类或其他任务的输出层。
右边的部分介绍了时间卷积网络(Temporal Convolutional Network,TCN),这是一种处理时间序列数据的网络架构。它显示了不同层的扩张卷积(dilated convolutions),这种卷积可以捕获时间序列数据的多尺度信息。
CNN的能力在于其学习局部静态结构的能力,通过局部化的卷积滤波器,并将它们组合起来形成多尺度的层次结构模式。
M. M. Bronstein, J. Bruna, Y. LeCun, A. Szlam, P. Vandergheynst在2017年发表的“Geometric Deep Learning: Going beyond Euclidean data”。这篇论文讨论了如何将深度学习扩展到传统的欧几里得数据类型之外,特别是到图数据,这直接与图卷积神经网络相关。
论文地址:Geometric Deep Learning: Going beyond Euclidean data
4、CNN的关键特性和它们在处理非欧几里得数据时面临的挑战

- 局部化卷积滤波器的平移不变性:
- CNN中卷积滤波器的一个重要特性:平移不变性(或称为位移不变性),这意味着网络能够识别出图像中的特征,无论这些特征出现在图像的哪个位置。
- 上图中一只猫的图像在不同位置时,CNN能够识别到相同的特征,显示出对平移的不变性。
- X形状模板匹配:
- 右侧的图示显示了一个简单的模板匹配的例子,展示了如何通过滤波器来识别特定的模式(pattern),在这个例子中是一个“X”形状。
- CNN使用滤波器来识别和匹配特定的图案,这是图像处理中的一个基本操作。
- 非欧几里得领域的挑战:
- 一个有趣的问题:如何将卷积的概念推广到非欧几里得域,例如图(graph)数据?
- 图数据的不规则结构给定义图数据上的卷积带来了挑战,因为图中的节点并没有像像素那样的规则排列,每个节点可能有不同数量的邻居,这使得不能直接应用传统的卷积操作。
5、From CNN to graph CNN
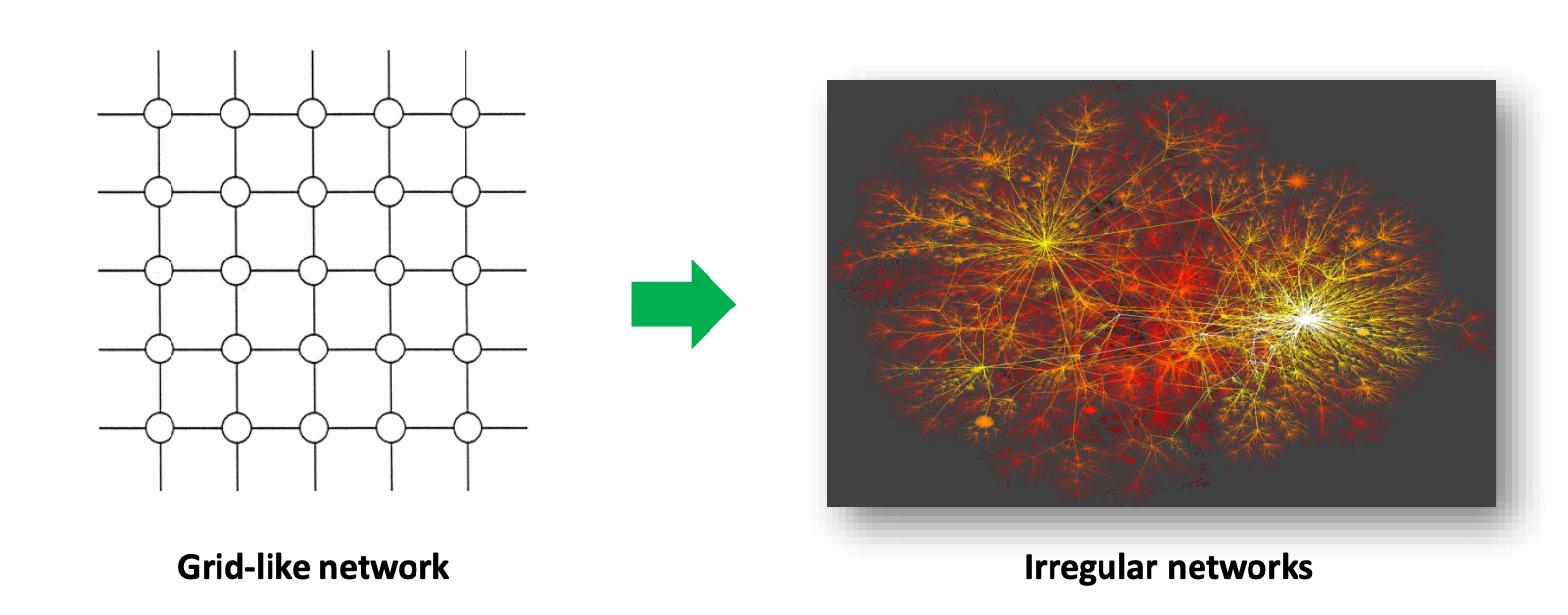
那么如何实现从传统卷积神经网络(CNN)到图卷积神经网络(Graph CNN)的转变呢?
左侧的图表显示了一个规则的网格状网络,这种结构是欧几里得数据的一个例子,像图像数据就是在这样的结构上处理的。在这种网络上,卷积操作是很好定义的,因为每个节点(比如像素)都有一个固定数量的邻居,这使得应用标准的卷积滤波器成为可能。
右侧的图像展示了一个不规则的网络,这种网络结构更贴近于现实世界中观察到的网络,如社交网络、蛋白质相互作用网络或其他类型的图。在这种不规则的网络中,每个节点可能有不同数量的邻居,这使得不能直接应用传统的卷积操作。
如何将CNN从处理规则的欧几里得数据(如图像)扩展到处理不规则的非欧几里得数据(如图数据)。这是深度学习领域的一个研究热点,因为它要求开发新的数学和计算工具来处理这些复杂的数据结构。
在开始图卷积之前,请先阅读下面这个通俗的例子,千万注意不要被下述公式、定理的具体细节绕进去。时不时回头来看一看这个例子,有助于“防沉迷”。
例子:
图卷积就像是一个“社交达人”,它在社交网络上了解每个人(节点)及其朋友圈(邻居)。在了解每个人的基础上,这位“社交达人”通过收集他们朋友圈中的信息(例如兴趣爱好、活动等),来形成对每个人更全面的认识。这就相当于在网络中进行了一次信息的汇总或“卷积”。
如果我们把每个人看作一个节点,每个人之间的关系看作是边,那么整个社交网络就可以被视作一个图。图卷积的目的,就是要从这个图中提取出有用的信息。
在数学上,这个过程可以通过一系列的转换和计算来实现,其中包括:
- 将每个人的信息(特征)与其朋友的信息结合起来。
- 通过某种方式来平衡自己的信息和朋友的信息的重要性。
- 将这种结合信息的方式应用于网络中的每一个人,从而得到一个全新的、更丰富的信息表示。
这样,通过图卷积,我们就能够更好地理解社交网络中每个人的角色和地位,或者在其他类型的图中理解每个节点的功能。
例子看完了,请开始阅读。
6、连续和离散情况下的卷积定义
卷积运算实际上就是两个函数 f f f和 g g g的数学操作,产生第三个函数 h h h。卷积在不同的上下文中有不同的定义:
- 连续情况:
- 卷积定义为两个函数乘积的积分,其中一个函数反转并移位。
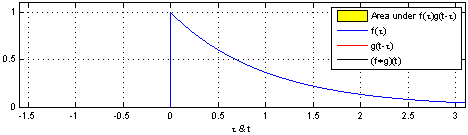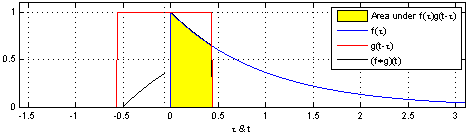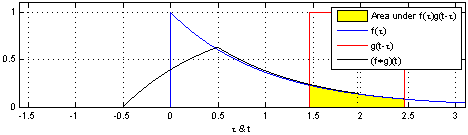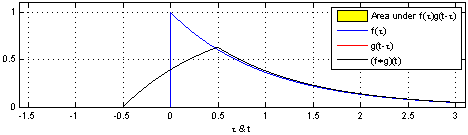
- 公式表示为: h ( t ) = ( f ∗ g ) ( t ) = ∫ f ( t − τ ) g ( τ ) d τ h(t) = (f * g)(t) = \int f(t - \tau)g(\tau) d\tau h(t)=(f∗g)(t)=∫f(t−τ)g(τ)dτ。
- 该图显示了连续卷积的一个例子,其中包括两个函数 f ( t ) f(t) f(t)和 g ( t − τ ) g(t-\tau) g(t−τ),以及它们的乘积 f ( t ) g ( t − τ ) f(t)g(t-\tau) f(t)g(t−τ)。
- 离散情况:
- 在离散情况下,卷积是两个函数乘积的总和,这在数字信号处理和图像处理中非常常见。
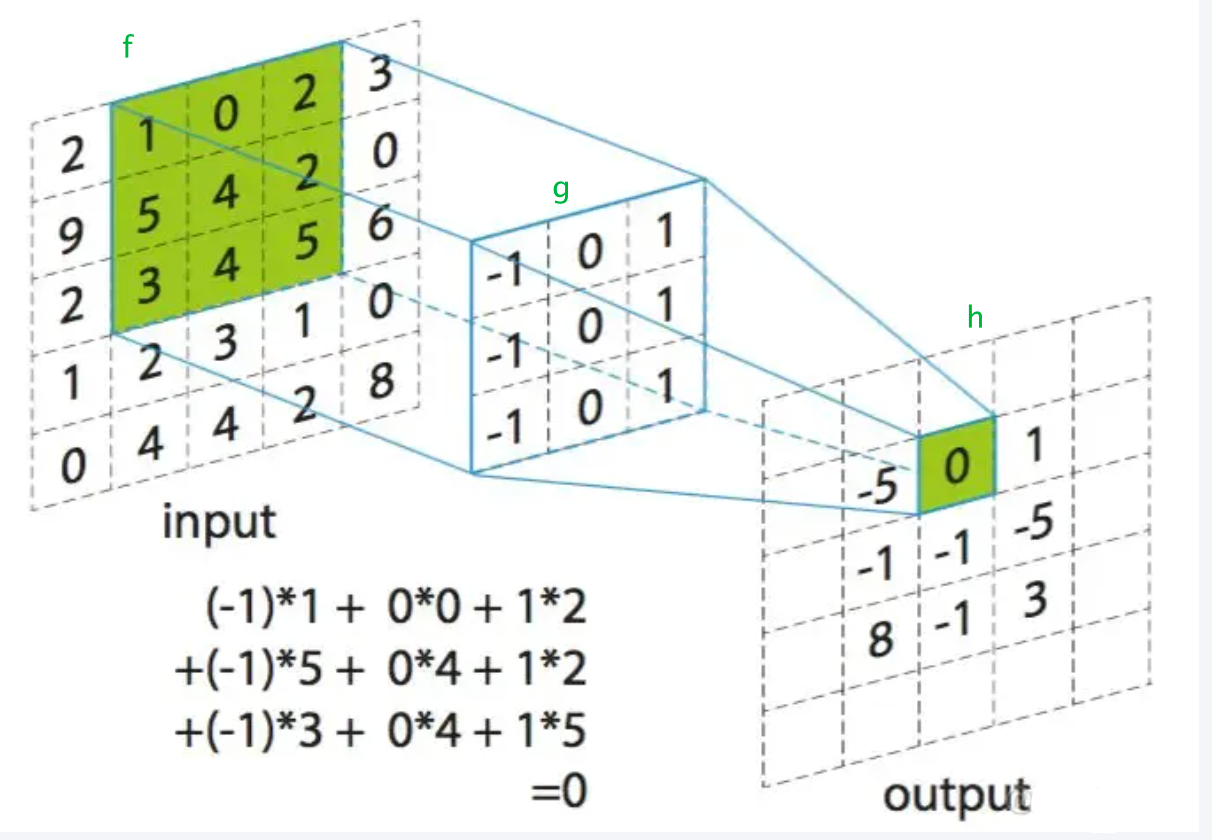
- 公式表示为: h ( x , y ) = ( f ∗ g ) ( x , y ) = ∑ m , n f ( x − m , y − n ) g ( m , n ) h(x, y) = (f * g)(x, y) = \sum_{m,n} f(x - m, y - n)g(m, n) h(x,y)=(f∗g)(x,y)=∑m,nf(x−m,y−n)g(m,n)。
- 用于卷积的两个函数 f f f和 g g g用矩阵表示。 f f f是一个较大的矩阵, g g g是一个较小的核(或滤波器),卷积操作涉及在 f f f上滑动 g g g并计算局部乘积的总和,得到输出 h h h。
7、谱方法和空间方法
- 谱方法:
- 该方法在谱域内定义卷积,即利用图傅立叶变换和卷积定理来实现。
- 主要挑战是在谱域定义的卷积滤波器在顶点域(即直接在图的节点上)不是局部化的。这意味着,谱域的滤波器可能难以捕捉图中节点的局部特征。
- 空间方法:
- 该方法在顶点域内定义卷积,通常被定义为目标顶点邻域内所有顶点的加权平均函数。
- 主要挑战是不同节点的邻域大小可能有显著差异,如在具有幂律度分布的图中,一些节点可能有很多邻居,而另一些节点则很少,这导致了卷积的不一致性和计算上的复杂性。
在图数据上定义和实现卷积是一个具有挑战性的问题,因为图数据的不规则性和复杂性。这两种方法尝试从不同角度解决这个问题,谱方法关注于图的全局频率属性,而空间方法更侧重于图的局部结构。
7.1 谱方法
7.1.1 谱方法中如何使用图拉普拉斯矩阵来定义图卷积
- 图的基本组成:
- 它定义了一个图
G
G
G为三元组
(
V
,
E
,
W
)
(V, E, W)
(V,E,W),其中:
- V V V是节点集合, n = ∣ V ∣ n = |V| n=∣V∣表示图中节点的数量。
- E E E是边集合。
- W W W是一个 n × n n \times n n×n的权重邻接矩阵,表示节点之间的连接强度。
- 每个节点与 d d d维特征相关联, X ∈ R n × d X \in \mathbb{R}^{n \times d} X∈Rn×d是节点的特征矩阵,其中 X X X的每一列代表一个在节点上定义的信号。
- 图拉普拉斯矩阵:
- 图拉普拉斯矩阵 L L L定义为 L = D − W L = D - W L=D−W,其中 D D D是度矩阵,一个对角矩阵,对角线上的元素 D i i D_{ii} Dii是节点 i i i的度(即节点 i i i连接的边的权重之和)。
- 归一化图拉普拉斯矩阵进一步定义为 L = I − D − 1 2 W D − 1 2 L = I - D^{-\frac{1}{2}}WD^{-\frac{1}{2}} L=I−D−21WD−21,其中 I I I是单位矩阵。
参考文章:
图卷积神经网络之-图拉普拉斯矩阵的解释
谱方法利用图拉普拉斯矩阵的特性来定义图上的傅立叶变换,进而定义卷积。这个方法考虑了图的全局结构,但这种定义在顶点域不是局部化的,这是实现有效图卷积操作的挑战之一。通过谱方法,可以在图数据上应用深度学习模型,例如图卷积网络(GCN)。
7.1.2 图傅立叶变换
图傅立叶变换,它是在图上处理信号的一种方法,类似于在传统欧几里得空间中的傅立叶变换。关键点如下:
- 傅立叶基:
图的傅立叶基是由图拉普拉斯矩阵 L L L 的一组正交归一化特征向量 { u l } l = 1 n \{u_l\}_{l=1}^n {ul}l=1n 组成的,这些特征向量按照与之对应的非负特征值 { λ l } l = 1 n \{\lambda_l\}_{l=1}^n {λl}l=1n 排序。
- 图拉普拉斯矩阵的对角化:
图拉普拉斯矩阵 L L L 可以被对角化为 L = U Λ U T L = U\Lambda U^T L=UΛUT,其中 U U U 是包含 L L L 的特征向量作为列的矩阵, Λ \Lambda Λ 是对角矩阵,其对角线上的元素是 L L L 的特征值。
- 图傅立叶变换:
图傅立叶变换是将图上的信号 x x x 转换到频域。这是通过将信号与每个特征向量相乘并累加来完成的,数学上表示为 x ^ = U T x \hat{x} = U^T x x^=UTx。
- 图傅立叶逆变换:
图傅立叶逆变换是图傅立叶变换的逆操作,用于将频域信号 x ^ \hat{x} x^ 转换回其在图上的空间表示。这是通过将频域信号与特征向量矩阵相乘来完成的,数学上表示为 x = U x ^ x = U \hat{x} x=Ux^。
图傅立叶变换是图信号处理领域的一个基础工具,它允许我们在图的频域中分析信号,并执行像滤波这样的操作。这在图卷积神经网络中是非常重要的,因为它允许网络学习图上的信号的频域特性。
参考文章:图卷积神经网络之-图傅立叶变换的解释
上述过程是知识铺垫,从现在开始真正进入图卷积!
7.1.3 在谱域内定义图卷积
如何在谱域内定义图卷积?图卷积的数学表达式和计算步骤是什么呢?
- 卷积定理:
- 卷积定理指出,两个信号的卷积的傅立叶变换等于它们傅立叶变换的点对点乘积(即哈达玛积)。
- 图卷积的定义:
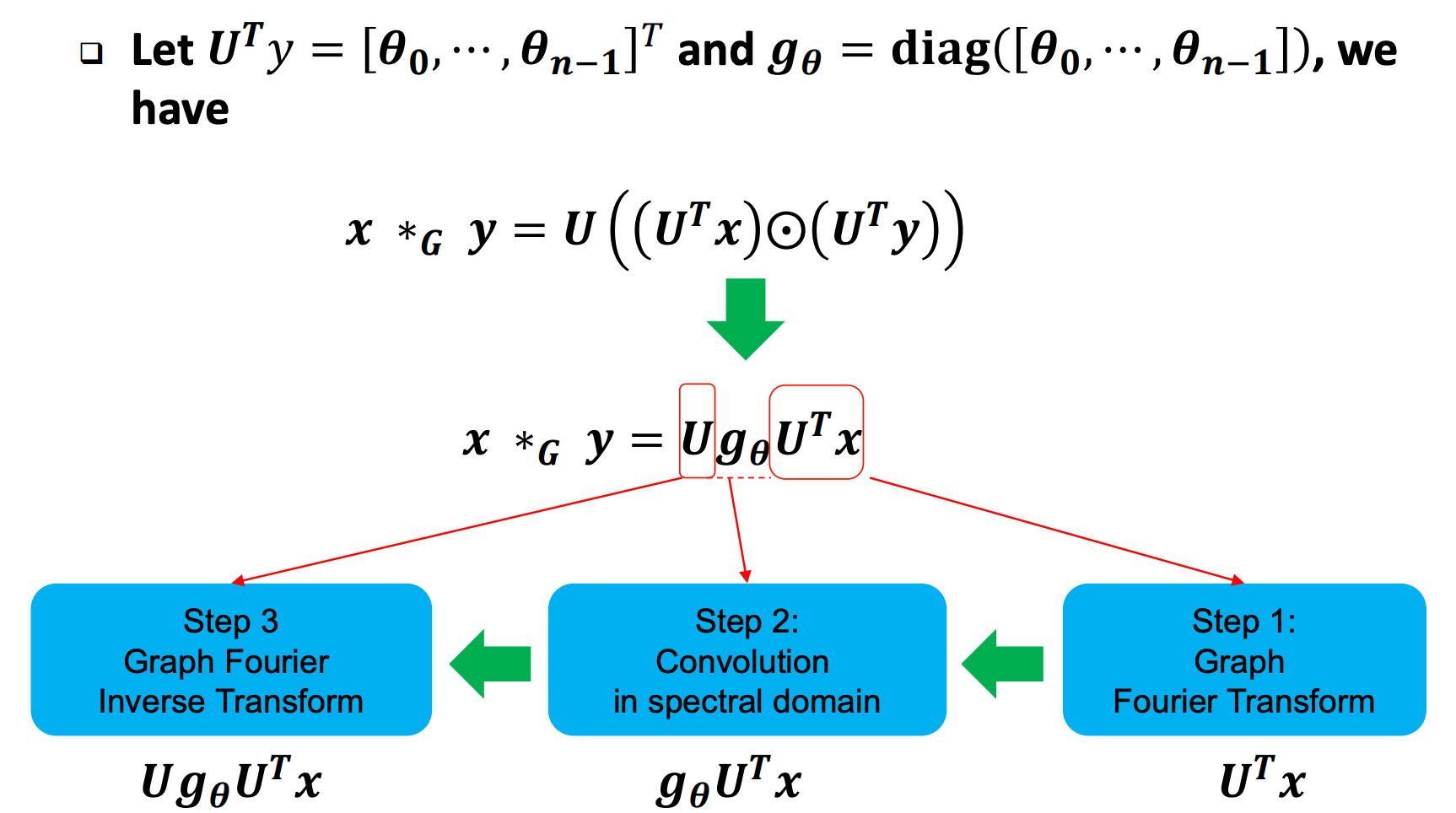
- 在图卷积的背景下,如果我们有一个输入信号 x x x 和另一个信号 y y y 作为滤波器,那么图卷积 x ∗ g y x *_{g} y x∗gy 可以写成 U ( ( U T x ) ⊙ ( U T y ) ) U((U^T x) \odot (U^T y)) U((UTx)⊙(UTy)),其中 ⊙ \odot ⊙ 表示元素乘积(哈达玛积), U U U 是图拉普拉斯矩阵的特征向量矩阵, U T y U^T y UTy 是滤波器在谱域的表示。
- 图卷积的步骤:
- 首先,我们计算输入信号 x x x 的图傅立叶变换 U T x U^T x UTx。
- 然后,我们计算谱域的滤波器 U T y U^T y UTy,其中 y y y 是空间域的滤波器信号。
- 接下来,我们执行两个信号的点对点乘积 ( U T x ) ⊙ ( U T y ) (U^T x) \odot (U^T y) (UTx)⊙(UTy)。
- 最后,我们应用图傅立叶逆变换 U U U 到结果上,得到最终的卷积结果。
幻灯片下方的图示说明了这个过程,其中 U T x U^T x UTx 是信号 x x x 在谱域的表示, g θ g_{\theta} gθ 是对角矩阵,其对角线上的元素是滤波器 y y y 的图傅立叶变换。图中的步骤1表示计算 U T x U^T x UTx,步骤2表示计算卷积 g θ ⊙ U T x g_{\theta} \odot U^T x gθ⊙UTx,步骤3表示应用逆变换 U g θ U T x U g_{\theta} U^T x UgθUTx 来得到卷积后的信号在图的空间域中的表示。
这种方法允许我们在图上执行卷积操作,这对于像图卷积网络这样的图深度学习模型来说是基础。通过这种方式,我们可以在图的节点上有效地应用和学习滤波器。
总结:
图卷积是一种在图结构数据上定义的卷积操作。与传统的卷积神经网络在规则的网格数据(如图像)上应用卷积核不同,图卷积旨在处理图数据,其中数据点(即图的节点)可以具有不同数量的相邻点并且结构不规则。图卷积的目标是能够捕获节点的特征以及它们之间的关系。
在数学上,图卷积可以通过多种方式定义,但其中一种流行的定义是利用图的谱理论,也就是通过图拉普拉斯矩阵的特征分解来定义。
假设我们有一个图 G G G,其图拉普拉斯矩阵为 L L L。在谱域中,我们可以通过以下步骤进行图卷积:
-
特征分解:
- 计算图拉普拉斯矩阵 L L L 的特征值和特征向量,得到 L = U Λ U T L = U\Lambda U^T L=UΛUT,其中 U U U 是特征向量组成的矩阵, Λ \Lambda Λ 是对角线上是特征值的对角矩阵。
-
图傅立叶变换:
- 对于图上的信号 x x x,其图傅立叶变换是 x ^ = U T x \hat{x} = U^T x x^=UTx。
-
卷积定理:
- 图卷积的一个关键概念是卷积定理,它指出两个信号的卷积等价于它们的傅立叶变换的点乘积的傅立叶逆变换。
-
图卷积:
- 给定图上的两个信号 x x x 和 y y y,图卷积 x ∗ g y x *_{g} y x∗gy 定义为 U ( ( U T x ) ⊙ ( U T y ) ) U((U^T x) \odot (U^T y)) U((UTx)⊙(UTy)),其中 ⊙ \odot ⊙ 表示元素乘积。如果 y y y 作为滤波器,则 U T y U^T y UTy 可以视为滤波器在谱域中的表示。
-
图卷积的实际计算:
- 实际上,直接计算 U T y U^T y UTy 可能非常昂贵,特别是对于大图。因此,通常会使用参数化的方法,例如定义一个参数化滤波器 g θ g_{\theta} gθ,这样我们就可以通过简化的形式 U g θ U T x U g_{\theta} U^T x UgθUTx 来计算图卷积,其中 g θ g_{\theta} gθ 是对角矩阵。
7.2 谱方法的缺点及改进
7.2.1谱图卷积神经网络的一些主要缺点
-
需要拉普拉斯矩阵的特征分解:
- 谱图CNN的一个关键步骤是计算图拉普拉斯矩阵的特征向量,这些特征向量在卷积操作中被直接使用。特征分解是一个计算密集的过程,特别是对于大型图。
-
高计算成本:
- 与图的傅立叶基 U U U 的乘法运算具有 O ( n 2 ) O(n^2) O(n2) 的时间复杂度,其中 n n n 是图中节点的数量。这意味着对于大图,这个操作可能非常耗时。
-
在顶点域不是局部化的:
- 在顶点域中,谱方法定义的卷积滤波器不是局部化的,这意味着它们不能捕捉到图中节点的局部邻域结构。这限制了模型捕捉局部模式的能力,并可能影响其在某些任务上的表现。
7.2.2 改进的谱图神经网络
ChebyNet,这是一种改进的谱图卷积神经网络,它通过多项式近似来参数化卷积滤波器,以解决传统谱图CNN所面临的一些挑战。
-
滤波器参数化:
- g θ g_{\theta} gθ 表示图卷积的滤波器,它是以对角矩阵的形式表示的,对角线上的元素是 [ θ 0 , … , θ n − 1 ] [\theta_0, \ldots, \theta_{n-1}] [θ0,…,θn−1]。
- 这个滤波器被参数化为一个多项式函数 g β ( Λ ) g_{\beta}(\Lambda) gβ(Λ),它是拉普拉斯矩阵的特征值 Λ \Lambda Λ 的函数。这里, Λ \Lambda Λ 是一个对角矩阵,对角线上的元素是特征值 [ λ 1 , λ 2 , … , λ n ] [\lambda_1, \lambda_2, \ldots, \lambda_n] [λ1,λ2,…,λn]。
-
多项式近似:
- g β ( Λ ) g_{\beta}(\Lambda) gβ(Λ) 被定义为一个 K K K 阶多项式,其中 β k \beta_k βk 是多项式的系数, Λ k \Lambda^k Λk 表示 Λ \Lambda Λ 矩阵的 k k k 次幂。
- 这个多项式近似允许滤波器仅依赖于 K K K 个系数,而不是 n n n 个(其中 n n n 是图中节点的数量),这显著减少了模型的自由参数数量。
-
ChebyNet卷积:
- 图卷积操作 x ∗ g y x *_{g} y x∗gy 在ChebyNet中被表示为 U g β ( Λ ) U T x U g_{\beta}(\Lambda) U^T x Ugβ(Λ)UTx,这里 U U U 是特征向量矩阵。
- 这可以进一步简化为 ∑ k = 0 K − 1 β k L k x \sum_{k=0}^{K-1} \beta_k L^k x ∑k=0K−1βkLkx,其中 L L L 是图拉普拉斯矩阵,而 L k x L^k x Lkx 表示将拉普拉斯矩阵 L L L 应用于信号 x x x k k k 次。
这种方法的优势在于它避免了直接对拉普拉斯矩阵进行特征分解,从而降低了计算成本。同时,由于多项式的递归性质,它可以高效地计算,并且滤波器在顶点域中具有局部性,这意味着滤波器可以捕捉节点及其近邻的局部特征。
论文地址:Convolutional Neural Networks on Graphs
with Fast Localized Spectral Filtering
参考:























 7194
7194

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










