论文阅读：Vehicle-Motion-Constraint-Based Visual-Inertial-Odometer Fusion With OnlineExtrinsicCalibration

前言

最近关注外参标定相关的研究，Vehicle-Motion-Constraint-Based Visual-Inertial-Odometer Fusion With Online Extrinsic Calibration发表在2023年的IEEE SENSORS JOURNAL上，是摄像头、惯性测量单元 和车轮里程计的多传感器融合定位工作，对于外参在线标定这个问题有着比较全面的研究，尤其是关于外参标定可观测性这块是我最近的研究兴趣，这篇文章有着不错的解决思路，因此对这篇文章的内容做一个介绍，希望能和大家一起讨论思考。

一、问题背景

GNSS在城市山谷、隧道、地下车库等 GNSS 退化环境中无法正常工作。相机、惯性测量单元（IMU）和里程表（也称为车轮编码器）的融合被认为是一种低成本且易于构建的地面车辆解决方案。在这样的融合框架中，参数的良好初始化非常重要，因为系统是非线性的并且对初始值敏感。此外，高性能定位依赖于传感器之间精确的外部参数。否则，将会引入额外的错误并且整体性能将会下降。

本文使用基于优化的方法，由于优化方法对初始值敏感，因此在进入优化过程之前需要进行良好的初始化。考虑到校准板的使用复杂且耗时，在线校准方法被开发来估计系统运行时的外参，该方法不需要校准板，并且已在学术界流行。里程表测量的预积分会比 IMU 引入更多的误差，特别是在车辆以一系列频繁变化的速度（例如启动和停止）行驶的情况下，因此引入车辆运动约束，通常称为非完整约束（NHC）和杠杆臂补偿。

二、理论流程

1、NHC和杠杆臂补偿

NHC可以被建模为，，但是真实估计值并不是完全为0，引入高斯噪声有：

此外，NHC还意味着车身框架原点处的速度始终与车身前进速度（本文中的车轮速度）一致。对于差速转向车辆，车架原点位于车身中心，而阿克曼转向车辆车架原点位于后轮中点。此外，未放置在车身框架原点的其他传感器（例如 IMU）的速度会受到 EP 平移的影响，这被称为杠杆臂效应。杠杆臂补偿表示IMU框架和里程表框架之间的坐标变换，如下图所示。考虑到里程表输出正是车辆的前进速度，因此我们将里程表框架视为车身框架本身。基于NHC和杠杆臂效应补偿，我们可以推导出IMU框架和里程表框架之间的速度关系

2、鲁棒初始化

我们提出了一种视觉-惯性-里程计联合初始化方法来估计初始参数，包括单目视觉尺度、重力、IMU 偏差、速度以及 俯仰和偏航外参分量。由于与里程计测量的融合，可以很好地提高单目视觉尺度恢复和其他参数的初始估计。考虑到地面车辆在道路上停车和行驶的两种典型场景，我们提出了一种分步初始化方法，充分利用上述场景中的静态和动态条件，以提高鲁棒性和有效性。

（1）静态初始化：重力、陀螺仪零偏、Pith轴外参

利用车辆停车时的静态状态来估计重力矢量以及从 IMU 坐标系到世界坐标系的旋转矩阵，我们收集停车状态下的加速度计数据，并将其平均值作为IMU坐标系中的初始重力矢量，记为gb init。世界坐标系中的重力矢量定义为 gw = [0, 0, G]T ，其中 G 是局部重力的大小。根据 Rodrigues 旋转公式[29]，Rw b 可以通过 gb init 和 gw = [0, 0, G]T 计算出来，因此，我们有

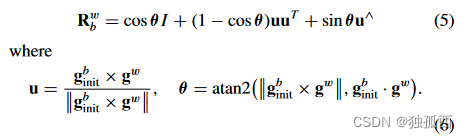
然后，IMU坐标系中的实际重力矢量gb可以计算为

此外，本文假设车辆一般停在近似平坦的表面上，因此 Rw b 的横滚和俯仰分量可以被视为 IMU 里程表 EP 的同一部分。因此，Rb o 可以写为

此外，由于陀螺仪的输出在静态下应为零，因此我们首先通过获取其平均值 ̄ ω 来估计 bω 和重力

然后，我们使用估计的 bω 在后续过程中对 IMU 测量进行预积分。与 VINS-Mono 的陀螺仪偏置初始化相比，我们的方法更适合车辆，因为当车辆直线起步时旋转运动并不常见，但在 VINS-Mono 中需要进行鲁棒估计。

（2）动态初始化：视觉尺度、IMU速度、Yaw轴外参

当车辆开始行驶时，我们进行动态初始化以获得视觉尺度和初始偏航分量外参。我们在本文中不估计加速偏差，因为在初始化期间通常没有足够的动机。首先，我们在滑动窗口 W 中收集多个视觉帧以限制计算成本，并使用初始 IMU 偏差进行预积分，如 [30]。我们假设 IMU 偏差在初始化过程中是恒定的。同时，初始的大规模相机位姿（̄ pcv k ,qcv k,k ∈ W）通过仅视觉结构恢复为[9]剂量。然后，我们执行视觉惯性里程计对齐以恢复初始视觉比例、IMU 速度和方向的偏航分量。

首先，视觉测量通过初始相机位姿和视觉尺度参数与 IMU 预积分对齐。考虑滑动窗口中的两个连续帧bk和bk+1，我们有以下位置与积分和速度预积分表达式

然后，我们将里程表测量值与 IMU 测量值对齐。等式（2）表示里程计测量值和 IMU 测量值之间的关系。考虑到 (8)，(2) 可以写为 

值得注意的是，我们在这里不估计平移 pb o ，因为初始化过程通常需要很短的时间，并且没有很大的动机来获得良好的平移估计。因此，我们在初始化过程中修复翻译 pb o = [0, 0, 0]。这种初始化过程中的估计变量定义为

将式(12)中的第k帧和第k+1帧代入式(10)，可得到视觉惯性里程计对准残差

由于我们需要估计旋转矩阵Row，因此我们根据上述残差制定非线性最小二乘问题

可以看出，旋转矩阵Row仅代表方向的偏航分量。因此，我们需要定义一个变量更新规则，以确保流形中只有偏航分量可以被优化。与[10]类似，我们有

另外，为了保证优化过程中视觉尺度s始终为正，我们利用了指数函数的属性，因此更新规则定义为

估计器收敛后，IMU-里程计外在旋转矩阵Rb o 可以通过式（8）用Rw b 和最优Row 计算得到。然后，它将成为非线性优化过程中的初始值。另外，IMU速度vbk bk 也可以通过式(12)恢复。总体而言，由于轮速在短时间内是准确的，因此与VINS-Mono相比，该方法不仅可以增强初始化性能，而且可以通过减少估计变量来提高鲁棒性。

3、非线性优化

由于 IMU 固定在车辆上，因此可以认为两个坐标系下的方向变化是一致的。需要说明的是，Rb o 的侧倾分量是不可观测的，因为一轮编码器里程表可以只提供车辆的前进速度：

因此，在非线性优化中只能估计Rb o 的俯仰和偏航分量。此外，很明显，从车辆坐标系到 IMU 坐标系的平移的 z 轴 po b 也是不可观测的，因为地面车辆通常没有垂直运动。为了消除不可观测性的影响，我们估计po b 而不是pb o。其与 pb o 的关系可写为

与[6]类似，我们制定了一个MAP估计问题来实现视觉、惯性和里程计融合，如图5所示。同时，全状态向量定义为

然后，我们最小化由马哈拉诺比斯距离加权的测量残差来解决MAP估计问题为车辆运动约束残差，由IMU预积分残差δαbk bk+1 、δβbk bk+1 、δγ bk bk+1 、δba 、δbω 和里程表杆臂补偿残差δvodo 组成。 IMU 预积分残差详细推导自[6]，而里程表残差可推导自(2)[32]。由于里程表杠杆臂补偿残差与 IMU 测量相关，因此我们将它们的残差一起构建。 gw 表示世界坐标系中的重力矢量。 1tk表示第k帧和第k+1帧之间的时间间隔。 ˆ αbk bk+1 、 ˆ β bk bk+1 和 ˆ γ bk bk+1 分别是相对于位置、速度和旋转的 IMU 预积分。 Rb o 是 qb o 的旋转矩阵。 ˆ vo bk+1 和 ˆ ωbk+1 分别表示第 k 个关键帧处车辆速度的实际值和陀螺仪的原始输出。 rp 和 rC(ˆ zcj l , X ) 分别是边缘化先验残差和视觉重投影残差。

我们还推导了所提出的 IMU 里程表残差的误差传播协方差。由于里程表测量残差没有采用预积分的形式，因此单独构建其噪声协方差矩阵，因此IMU-里程表残差的噪声协方差矩阵定义为

其中Pimu是IMU预积分残差的噪声协方差矩阵，与[6]中所示相同，而里程表残差Podo的噪声协方差矩阵可以写为

考虑到大角度转弯时NHC不能完全满足，意味着y轴NHC噪声协方差σ 2 y 会趋于增大。因此，我们选择根据车辆的运动状态自适应调整σ 2 y 。文献[33]指出y轴NHC噪声的大小同时受到前进速度和转弯运动的影响。受此启发，我们在转弯时动态改变 σy，但将其设置为与 x 轴 NHC 噪声 σx = 0.1 相同，如下所示：

另外，我们设置一个阈值σth = σx来约束σy的最小值，以避免停车时出现零值

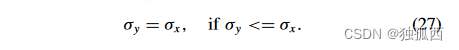
基于我们提出的 IMU 里程计残差，可以使用 δvodo 的雅可比相对于 Rb o 和 po b 轻松在线校准 EP

‘如上所述，po b 的 z 轴分量以及 pb o 的滚动分量是不可观测的。因此，我们可以在非线性优化过程中修复它们以保持稳定性。为了确保仅估计 EP 的俯仰、偏航、x 和 y 分量，我们分别定义 Rb o 和 po b 的变量更新规则，如下所示：

4、基于可观测性识别的在线外参标定

众所周知，外参标定不仅关系到系统的稳定性，还关系到参数的可观性。在本节中，我们通过考虑停车和转弯两种车辆运动状态来研究外参标定的可观测性。然后，我们根据可观测性判断和上述运动检测来校准EP，以确保稳定性和准确性。

（1）可观测性判断

根据地面车辆转弯和停车的运动特性，提出了可观测性判断的两个定理。

定理1：当车辆在直线道路上行驶时，只能观测到Rb o (2 DoF)的俯仰和偏航分量。考虑式(23)中里程表杆臂补偿残差δvodo，忽略噪声影响，令δvodo = 0，有

当车辆在直线道路上行驶时，陀螺仪的输出可以视为其偏置，因此，

可以看出，(32) 只包含旋转 Rb o 而不是平移 pb o，这意味着在直路上只能观察到旋转。此外，(19)表明旋转矩阵的滚动分量也是不可观测的。因此，在车辆进入第一个弯道之前，我们启用俯仰和偏航校准，但禁用平移校准。

定理2：当车辆转弯时，po b 的x和y分量以及Rb o 的俯仰和偏航分量是可观测的。由于转弯时不能满足式（31），因此可以同时激发旋转和平移误差，如式（23）所示。受益于优化框架的边缘化，转弯后平移仍然可观察到。因此，我们在车辆进入第一个弯道时同时启用外旋转和平移校准，并在整个过程中保持启用状态。值得注意的是，转动检查不仅对于估计的稳定性很重要，而且对于参数的收敛也很重要。

定理3：停车时所有外参都是不可观测的。当车辆停车或处于静止状态时，IMU和里程表的输出都接近于零，这意味着外参的方向和平移都是不可观测的。因此，我们修复它们是为了估计器的稳定性以及另一个参数（例如 IMU 偏差）的准确估计。

（2）运动状态检测

根据上述分析可知，车辆运动状态极大地决定了估计参数的可观性。因此，正确的车辆运动状态检测对于外参标定至关重要。本文主要研究转弯状态和停车状态的检测方法。为了清楚起见，我们将当前车辆运动状态表示为S，转弯状态表示为Sturn，直行状态表示为Sline，停车状态表示为Spark，行驶状态表示为Sdrive，其中包括转弯状态和直行状态状态。

a）转动状态检测：由于外部校准将额外的变量引入估计器（如（23）），系统的稳定性变得具有挑战性。一些早期的相关工作如[19]指出，只有当加速度计偏差收敛时，视觉惯性里程计系统才会受到良好的约束，这要求车辆行驶通过第一个弯道。为了确保标定 EP 时的系统稳定性，我们在本文中提出了一种有效且鲁棒的转动状态检测方法，该方法同时利用角速度和相对旋转，如算法 1 所示。首先，我们设置一个滑动大小为 Nturn 的窗口 Wturn 来收集角速度 ω。然后，我们计算滑动窗口中的平均值 ̄ ω 。给定阈值 ωth，当 ̄ ω > ωth 时，车辆可视为转弯。此外，我们的实验表明，只有当车辆以大角度转弯时，加速度计偏差才开始收敛。因此，利用相对旋转角度来辅助检测。一旦通过角速度条件检测到转动，我们将相对旋转的偏航角的变化累积为1ψ。给定阈值ψth，当1ψ>ψth时，可以认为车辆发生了大角度转弯。需要说明的是，只有̄ω满足条件才是累加的相对旋转角度，才能保证车辆始终处于转弯状态。当1ψ满足条件后，即可认为转向状态检测成功。

对于上面提到的阈值参数ωth和ψth，我们通过经验和实验来确定它们的值。在我们提出的算法中，使用角速度的目的是确定车辆开始转向的时间，而转向角度的变化表示转向的幅度，这与加速度计偏差的收敛密切相关。因此，为了提高检测的灵敏度，我们在实验中将ωth设置为较小的值0.05 rad/s。为了确定ψth的值，我们在满足角速度条件后，从Kaist数据集序列urban26中统计三个轴上的1ψ和加速度计偏差的数据，如图6（a）所示。可以看出，当转角达到35°左右时，偏差开始收敛。因此，我们将ψth设置为35°，这样可以保证检测转弯时加速度计偏差的收敛。评估其普遍性选择阈值后，我们还收集了现实世界地面机器人的实验数据，如图 6（b）所示。 Kaist数据集数据代表高速场景，而地面机器人数据说明了参数在低速场景下的有效性。不难看出，选取的阈值仍然是合理有效的。

b）停车状态检测：值得注意的是，由于不同车辆平台的车轮速度差异很大，因此我们仅利用IMU进行停车状态检测。此外，所提出的初始化方法要求车辆在起步时有明显的加速度变化才能进行良好的估计，使用IMU进行停车状态检测更合适，因为它可以直接获取加速度数据。如算法2所示，我们使用加速度计数据和滑动窗口来检测停车状态。为了在静态初始化中正确检测停车状态，我们设置一个时间为2T的滑动窗口，并将其分为两个子窗口w1，w2，w1 ∈ (T, 2T ), w2 ∈ (0, T )。然后，我们可以通过将两个子窗口aw1和aw2的加速度计测量值a的标准差与阈值stdth进行比较来检测停车状态或启动运动，具体来说，如果aw1大于stdth而aw2小于stdth，则我们假设车辆在w1处开始移动，但在w2处保持静止，那么我们可以使用w2的数据来初始化系统。否则，如果 aw1 小于 stdth，则意味着车辆仍然静止，我们滑动窗口直到检测到启动状态。反之，只有aw1和aw2都小于阈值stdth，才能认为车辆已经停止。类似地，我们通过从两个子窗口收集加速度及其标准差的数据来确定stdth的值，如图7（a）所示。可以看出，从第2秒开始加速度变化明显，这意味着车辆从停车开始。 aw1 同时也变化很大，而 aw2 仍然接近于零。根据我们的算法，可以知道起始运动被成功检测到。更具体地说，aw1 的变体在此期间具有最大值 0.35。基于上述，我们将stdth设置为0.2，以保证检测的灵敏度。另外，根据加速度的变化，车辆在第36秒左右停车，此时aw1和aw2均低于阈值stdth。此外，我们评估了地面机器人数据中选定的阈值以说明普适性，如图 7（b）所示。这表明我们的方法在低速和高速场景下都能有效检测停车状态。

三、实验方案

在本节中，我们在不同场景中进行实验来评估我们的方法。首先，我们进行仿真实验来评估所提出的在线外部校准方法的性能，因为所需的运动环境和EP可以由我们自己提供，这有利于我们的实验。然后，我们使用自动驾驶公共数据集评估初始化和定位的性能。如上所述，我们在实验中仅融合车轮编码器的前进速度。我们的实现基于 VINS-Fusion，所有实验均在具有 Intel i9-12900H CPU 和 16G RAM 的笔记本电脑上进行。

1、仿真实验

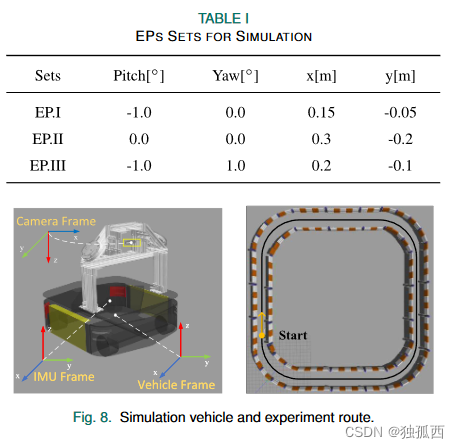
我们参考BetaGo[36]的工作，通过Gazebo仿真构建了仿真环境和仿真车辆模型。模拟车辆及实验路线如图8所示。车辆配备D435i相机模型（全局快门和30 Hz）、消费级IMU（100 Hz）和可反馈轮速的差速底盘在 100 赫兹。底盘的中心作为baselink的原点。实验路线有4条直线和4个90°拐角。车辆以1.5 m/s的线速度和0.5 rad/s的角速度向前移动。为了获得良好的收敛效果，实验路线绕了很多圈。我们设置了三组不同的 EP 进行模拟实验，如表 1 所示。由于滚动和平移和 z 轴平移是不可观测的，因此我们仅在方向上设置俯仰和偏航，在平移中设置 x 和 y。在仿真实验中，我们设置NHC噪声权重系数knhc = 0.1。

我们进行了实验来评估外部校准在初始化和后端优化方面的性能，其中分别讨论了初始估计 EP 的必要性和校准精度。

1）初始化时的外参标定：如上所述，EP的初始估计不仅影响融合方法的稳定性，而且影响外参标定的性能，特别是对于方向的偏航分量。在本节中，我们进行实验来评估不同偏航初始值对轨迹的影响。选择EP集EP.II完成实验，俯仰角和偏航角均为0°。首先，我们设置四种方案进行比较：1）初始化EP； 2）固定初始偏航角为30°； 3）固定初始偏航角为60°； 4) 固定初始偏航角为90°。由于方案2）至4）与给定的groundtruth相比设置了不同的偏航值，因此我们使用[9]中的方法来完成初始化。系统初始化后，我们在后端优化中启用在线外参标定，以修正偏航初始值的误差。然后，我们比较了四种方案产生的轨迹，如图9所示。可以看出，轨迹起点处存在较大差异。随着偏航初始值的增加，起始点附近的轨迹偏差从vio-2增大到vio-3，即使导致轨迹vio-4发散。然而，由于初始化时对偏航的有效估计，我们提出的初始化方法（vio-1）产生的轨迹在开始部分比其他方法更平滑。总之，良好的 EP 方向初始值是必要的，误差值会严重影响轨迹，甚至导致发散。我们还收集了上述四种方案在 10 次运行中的数值初始化结果，以定量地说明我们的方法，如图 10 所示。可以看出，方案 1）中的偏航估计可以在 0° 左右，误差范围为约2°，而方案4）的结果也显示出类似的现象。此外，方案 2) 和 3) 中的偏航估计显示出约 4° 的误差范围，但仍然可以在真实值附近。事实上，我们的实验表明偏航初始化误差范围在15°以内是可以接受的。总的来说，上述结果表明我们的初始化方法对于不同类型参数的外在校准是有效且稳健的。

  

2）非线性优化中的外部校准：我们使用所提出的可观测性感知方法在线估计非线性优化中的EP。结果如图 11-13。在这三个图中，方向参数是从车辆开始时估计的，而平移参数在开始时固定为零，并在满足转弯条件时开始估计。同时，可以看出所有估计参数都可以收敛到真实值。此外，所有三个 EP 组的几乎平移校准误差约为 0.02 m。对于旋转标定，EP.I 和 EP.III 的标定误差较小，约为 0.05°，而 EP.II 的标定误差较大，为 0.1°。这是因为EP.II的俯仰角和偏航角均为零，外在旋转校准的动力不足。总体而言，实验结果表明，我们的具有可观测性判断的校准方法可以在不同类型的 EP 中实现准确且一致的估计。这也证明了所提出的方法是有效且鲁棒的。
 

2、公开数据集实验

Kaist 数据集用于完成本节中的实验。该数据集捕获大都市地区、复杂建筑、住宅区和其他城市环境的特征。传感器配置包括立体相机（全局快门和 10 Hz）、消费级 IMU（100 Hz）、车轮编码器（每轮 4096 个脉冲和 100 Hz）以及其他各种位置传感器。 groundtruth是基于融合车轮编码器的SLAM算法生成的，FOG、VRS-GPS 和激光雷达测量。此外，值得注意的是，数据集中包含大量停车和出发地点，这可以对所提出的方法进行强有力的评估。在公共数据集实验中，我们设置NHC噪声权重系数knhc = 1.0。

1）初始视觉尺度恢复：为了评估初始化的性能，我们将我们的方法与 VINS 的初始化方法和开源视觉惯性轮编码器融合方法 VIW-Fusion [20] 进行比较。考虑到我们的方法静态初始化的要求，我们在Kaist数据集的urban26、urban28和urban30序列中选择了六个具有停车状态的地点，如图14所示，完成实验并同时执行其他两种方法观点。我们将滑动窗口的大小设置为 15，并保持 VINS 的其他公共参数相同。由于在不同起点估计的视觉尺度并不完全相同，为了做出合理的评估，我们将恢复的轨迹与地面实况进行比较。我们定义具有恢复尺度的视觉姿势的平移为trec，对应的groundtruth为tgt，那么尺度恢复误差可以定义为

比较结果如表二所示。可以看出，三种方法在urban26-1和urban28-3上都效果很好，误差在3%以内，因为这两个地方都有良好的视觉条件来估计视觉姿态，如图14所示。然而，我们的方法在其他四个地方表现更好，因为更多的车辆出现在摄像机前面，这导致启动时的视觉测量结果更差。特别是在urban28-1中，我们的方法只有2.73%的误差，而VIW-Fusion的误差更大，达到24.11%，甚至VINS初始化失败。总体而言，我们方法的所有实验点的初始化误差都保持在 3% 以内，这表明所提出的初始化方法更加稳健和有效。

2）定位精度比较：最后，我们用Kaist数据集的urban26序列的一部分（约3.6公里，覆盖了城市地区的大部分场景）定量评估了我们的融合方法在自动驾驶场景中的轨迹精度。为了评估在线外标定下的轨迹精度，我们设置了三种方法模式，分别对应于固定 EP、直接标定 EP 和通过可观测性分析标定 EP。此外，我们的方法与视觉惯性融合方法VINS-Fusion和VIW-Fusion进行了比较，这两种方法都提供在线校准EP的功能。考虑到车辆通常在平坦路面上行驶的假设，我们只评估水平位置误差，并使用绝对位姿误差（APE）来评估轨迹的全局一致性轨迹如图 15 所示，每种算法的均方根误差为 VINS-Fusion（单声道）79.764 m，带校准的 VIW-Fusion 45.684 m，不带校准的 VIWFusion 37.239 m，建议使用校准 1) 16.225 m，建议带校准 2) 12.637 m，建议不带校准 10.637 m。可以明显看出，我们的方法无论是在线外参校准还是固定 EP，都比 VINS-Fusion 和 VIWFusion 表现更好。此外，固定 EP 是我们最好的方法，因为准确的 EP 可以减少外部校准的大部分误差。对于在线校准，由于合理的校准环境，我们的可观测性分析方法比其他方法表现更好。综上所述，我们的方法在自动驾驶场景下的位置精度方面都表现良好，特别是在没有IMU-里程计EP先验知识的情况下，我们的方法可以在线校准EP，同时达到相当的精度。

3、真实世界实验

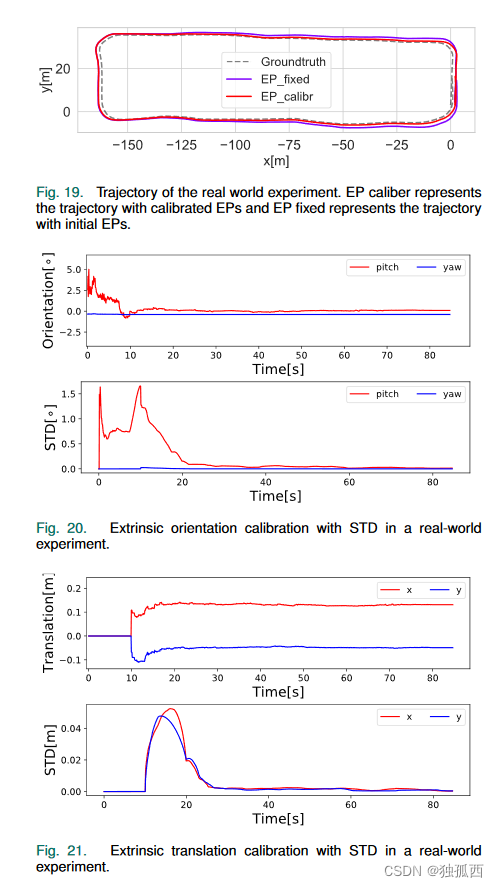
我们使用地面机器人进行现实世界的实验。硬件和框架如图16所示。地面机器人配备差速底盘和内置IMU（100 Hz）的D455立体相机（30 Hz）。轮速可以从底盘获得。相机-IMU（Rb c ，pb c ）的 EP 已预先使用 Kalibr 工具进行校准，并且我们通过所提出的方法在线校准 IMU-里程计 EP。这里，我们设置与公共数据集实验相同的NHC噪声权重系数knhc。为了证明我们方法的一致性，我们首先使用 90 米长的校准实验路线来校准 IMU 里程表 EP，如图 17 所示。然后，我们在另一个位置进行有和没有校准 EP 的位置精度实验。 408米长的路线如图18所示。具体来说，我们设置外在旋转的单位矩阵和外在平移的零向量作为初始参数。最后，我们比较上述两组EP生成的位置精度来评估我们的方法。在位置精度实验中，使用具有闭环的LIO-SAM [37]轨迹作为groundtruth。此外，我们使用绝对轨迹误差（ATE）来评估位置精度。位置结果如图19所示。可以清楚地看到，在线外参校准的轨迹比固定EP的轨迹更接近地面实况。在我们的实际实验中，前者的位置误差为 1.86 m (RMSE)，导致定位误差为 0.46%，而后者的位置误差为 1.19 m (RMSE)，导致定位误差为 0.29%。此外，无花果。图20和21显示了外在校准的收敛结果。由于 IMU 和车辆的坐标不同，导致方向相差 90°，为了清楚起见，我们将其转换为标准坐标以收集结果。为了证明收敛性能，我们还评估了 10 秒长滑动窗口中校准结果的标准偏差。结果表明，俯仰角收敛于约0.1°，标准差约为0.05°；偏航角收敛于约-0.1°，标准差约为0.005°。 x 轴平移收敛于约 0.12 m，而 y 轴平移收敛于 -0.05 m。两者具有相同的标准差，约为 0.002 m。可以看出，偏航分量比俯仰分量具有更好的收敛性。这是因为俯仰分量的动机要少得多，导致其可观测性比偏航差。总体而言，所有参数都设法在非常低的误差范围内收敛。总之，比较结果有力地证明了所提出的方法对于在线IMU里程表外在标定是有效且高效的。

四、创新总结

关注车辆运动约束，通常称为非完整约束（NHC）和杠杆臂补偿，并在基于过滤的框架中广泛应用于 IMU/里程计系统 [27] 和 GNSS/IMU 系统 [28]。NHC是指在不打滑或颠簸的情况下车辆的横向和垂直速度可以视为为零，而NHC的正确使用需要对IMU和车身之间的杠杆臂进行补偿[28]。值得注意的是，车辆运动约束设法建立基于速度的测量模型，这意味着它可以直接限制速度估计误差，而不需要积分到位移中。受此启发，与使用预积分不同，在本文中，利用车辆运动约束和里程计的速度测量来构建基于优化的视觉惯性里程计框架，该框架简洁有效。基于提出的框架，还研究了鲁棒初始化和在线 IMU 里程表校准以提高性能。主要贡献如下。

1）提出了一种基于车辆运动约束的具有鲁棒初始化的紧耦合视觉惯性里程计框架。该框架直接耦合里程计速度，不需要预先积分里程计测量结果，可以提高速度频繁变化场景下的性能。

2）基于所提出的框架设计了从粗到精的IMU里程表外在标定方法。它使我们能够在无需事先了解初始化过程的情况下获得初始 IMU 里程表 EP，并在后端优化中对其进行在线精细校准。该校准方法明确，不需要在预积分框架中进行线性化，从而获得更好的性能。

3）提出了一种可观测性感知的在线外在校准过程。它使我们能够通过车辆运动可观测性判断来确定IMU里程表外标定的有利条件，从而提高参数的收敛性和系统的鲁棒性。

在本文中，提出了一种基于车辆运动约束实现的地面车辆视觉惯性里程计框架。所提出的框架允许明确地在线校准 IMU 里程表 EP。还开发了一种可观测性感知方法来增强系统稳定性和在线外参校准的性能。此外，还开发了鲁棒的初始化算法以获得系统和EP的良好值。该方法的关键在于，它直接融合原始里程表速度测量值，而不是将它们预先积分到位移中。这不仅有利于精度，而且有利于在线外参校准。来自模拟、公共数据集和现实世界的各种实验表明，方法是有效的、稳健的，并且可以达到与其他最先进的方法相同的水平。方法的局限性在于，在长期定位中，陀螺仪的航向漂移仍然不能忽略。未来将通过结合陀螺仪和多轮编码器的航向测量来研究这方面。

对于可观测性的检测，是先分析哪几种运动状态会导致不可观测性，然后检测运动状态，设计算法来检测，本文的算法挺朴素的，基本就是阈值检测。