目录
〇、写在前面
- 往期文章传送门:
拉氏变换
控制系统的数学模型
时域分析法
根轨迹的绘制
根轨迹法分析系统性能 - 本文定位:复习
一、频率特性
1.1 线性系统的频率特性
仍然考虑RC电路为例:

由控制系统的数学模型所讲内容可知,系统的输入输出关系为: T d u O d t + u O = u i T\frac{du_O}{dt}+u_O=u_i TdtduO+uO=ui于是传递函数表示为: G ( s ) = 1 T s + 1 G(s)=\frac{1}{Ts+1} G(s)=Ts+11先前我们讨论了输入为阶跃信号、斜坡信号等输入时的响应。现在,如果我们将电路接入交流电,使得输入 u i = A s i n ( ω t ) u_i=Asin(\omega t) ui=Asin(ωt),并使 u O u_O uO 的初始值为 u O 0 u_{O_0} uO0,则 U O ( s ) = 1 T s + 1 [ U i ( s ) + T u O 0 ] = 1 T s + 1 [ A ω s 2 + ω 2 + T u O 0 ] U_O(s)=\frac{1}{Ts+1}[U_i(s)+Tu_{O_0}]=\frac{1}{Ts+1}[\frac{A\omega}{s^2+\omega^2}+Tu_{O_0}] UO(s)=Ts+11[Ui(s)+TuO0]=Ts+11[s2+ω2Aω+TuO0]反拉氏变换得: u o ( t ) = ( u O 0 + A ω T 1 + T 2 ω 2 ) e − t T + A 1 + T 2 ω 2 s i n ( ω t − a r c t a n ω T ) u_o(t)=(u_{O_0}+\frac{A\omega T}{1+T^2\omega^2})\text e^{-\frac{t}{T}}+\frac{A}{\sqrt{1+T^2\omega^2}}sin(\omega t-arctan\omega T) uo(t)=(uO0+1+T2ω2AωT)e−Tt+1+T2ω2Asin(ωt−arctanωT)所以: lim t → ∞ u o = A 1 + T 2 ω 2 s i n ( ω t − a r c t a n ω T ) \lim_{t \to \infty}u_{o}=\frac{A}{\sqrt{1+T^2\omega^2}}sin(\omega t-arctan\omega T) t→∞limuo=1+T2ω2Asin(ωt−arctanωT)可以看出,稳态输出幅值为: A ( ω ) = A 1 + T 2 ω 2 A(\omega)=\frac{A}{\sqrt{1+T^2\omega^2}} A(ω)=1+T2ω2A稳态输出相位为: ϕ ( ω ) = − a r c t a n ω T \phi(\omega)=-arctan\omega T ϕ(ω)=−arctanωT其中,负号表示滞后。
从这两个式子可以看出,输出响应的幅值和相位是频率
ω
\omega
ω 的函数。
由此可以引出频率特性定义:
输出信号与输入信号的傅氏变换之比成为频率特性,其中,输出与输入同频谐波分量幅值与输入幅值之比成为幅频特性,输出与输入同频谐波分量与输入信号相位差
ϕ
(
ω
)
\phi(\omega)
ϕ(ω) 叫相频特性,并且规定,当
ϕ
(
ω
)
<
0
\phi(\omega)<0
ϕ(ω)<0 时,称之为输出滞后,否则称之为输出超前。用公式表述为:
A
(
ω
)
=
∣
X
c
(
j
ω
)
X
r
(
j
ω
)
∣
=
R
e
2
+
I
m
2
A(\omega)=\lvert\frac{X_c(j\omega)}{X_r(j\omega)}\rvert=\sqrt{Re^2+Im^2}
A(ω)=∣Xr(jω)Xc(jω)∣=Re2+Im2
ϕ
(
ω
)
=
∠
X
c
(
j
ω
)
X
r
(
j
ω
)
=
a
r
c
t
a
n
I
m
R
e
\phi(\omega) = \angle\frac{X_c(j\omega)}{X_r(j\omega)}=arctan\frac{Im}{Re}
ϕ(ω)=∠Xr(jω)Xc(jω)=arctanReIm
1.2 不同算法之间的联系
微分方程—拉氏变换—>传递函数—反拉氏变换—>微分方程—傅氏变换—>频率特性
传递函数—令s=jw—>频率特性—辨识—>传递函数
二、奈氏图
2.1 绘制开环幅相曲线
例:已知:
G
(
s
)
H
(
s
)
=
10
s
(
s
+
1
)
(
10
s
+
5
)
G(s)H(s)=\frac{10}{s(s+1)(10s+5)}
G(s)H(s)=s(s+1)(10s+5)10绘制其奈氏图。
解:【这个绘制奈氏图,胡寿松课本上写的方法是将其分解为若干典型环节,然后判定每个环节的幅相情况,从而判断整体情况。这里我写了一种直接判定的方法,无需分解各个环节,过程长一些,但不需要记忆各个环节,而且每个式子表示的意义也很明显。】
首先写在前面,复习一个复变函数里的知识点,两个复数相乘得到结果的模等于两个复数模的成积,该结果的幅角等于两个幅角的和;两个复数相除的结果的模等于两个复数模相除,结果的幅角等于两个复数幅角的差。
化为尾一标准型,然后令
s
=
j
ω
s=j\omega
s=jω,得:
G
(
j
ω
)
H
(
j
ω
)
=
2
j
ω
(
j
ω
+
1
)
(
2
j
ω
+
1
)
G(j\omega)H(j\omega)=\frac{2}{j\omega(j\omega+1)(2j\omega+1)}
G(jω)H(jω)=jω(jω+1)(2jω+1)2
当
ω
=
0
\omega=0
ω=0 时(这个0不是0+,而是真正的0),
∣
G
(
0
)
H
(
0
)
∣
=
∞
|G(0)H(0)|=\infty
∣G(0)H(0)∣=∞
∠
G
(
0
)
H
(
0
)
=
0
−
0
−
0
−
0
=
0
\angle G(0)H(0)=0-0-0-0=0
∠G(0)H(0)=0−0−0−0=0关于这个相角为什么这样写,你看,分子是2吧,2在复平面上的点是(2,0),所以角度是0,分母上第一个因式是jw,当w=0的时候,对应在复平面上坐标是(0,0),也就是原点,所以角度是0,第二个因式(jw+1)当w=0的时候,对应在复平面上坐标是(1,0),所以角度是0,第三个因式(2jw+1)当w=0时,对应复平面上点是(1,0),所以角度是0。这三个都在分母上,所以是0-0-0-0=0。
当
ω
=
0
+
\omega=0^+
ω=0+ 时,
∣
G
(
0
+
)
H
(
0
+
)
∣
=
lim
ω
→
0
+
2
ω
1
+
ω
2
1
+
4
ω
2
=
∞
|G(0^+)H(0^+)|=\lim_{\omega\to0^+}{\frac{2}{\omega\sqrt{1+\omega^2}\sqrt{1+4\omega^2}}}=\infty
∣G(0+)H(0+)∣=ω→0+limω1+ω21+4ω22=∞
∠
G
(
0
+
)
H
(
0
+
)
=
lim
ω
→
0
+
(
0
−
π
2
−
a
r
c
t
a
n
ω
−
a
r
c
t
a
n
2
ω
)
=
0
−
π
2
=
−
π
2
\angle G(0^+)H(0^+)=\lim_{\omega\to0^+}{(0-\frac{\pi}{2}-arctan\omega-arctan2\omega)}=0-\frac{\pi}{2}=-\frac{\pi}{2}
∠G(0+)H(0+)=ω→0+lim(0−2π−arctanω−arctan2ω)=0−2π=−2π当
ω
=
∞
\omega=\infty
ω=∞ 时,
∣
G
(
∞
)
H
(
∞
)
∣
=
lim
ω
→
∞
2
ω
1
+
ω
2
1
+
4
ω
2
=
0
|G(\infty)H(\infty)|=\lim_{\omega\to\infty}{\frac{2}{\omega\sqrt{1+\omega^2}\sqrt{1+4\omega^2}}}=0
∣G(∞)H(∞)∣=ω→∞limω1+ω21+4ω22=0
∠
G
(
∞
)
H
(
∞
)
=
lim
ω
→
∞
(
0
−
π
2
−
a
r
c
t
a
n
ω
−
a
r
c
t
a
n
2
ω
)
=
−
3
π
2
\angle G(\infty)H(\infty)=\lim_{\omega\to\infty}{(0-\frac{\pi}{2}-arctan\omega-arctan2\omega)}=-\frac{3\pi}{2}
∠G(∞)H(∞)=ω→∞lim(0−2π−arctanω−arctan2ω)=−23π
对传递函数,令
s
=
j
ω
s=j\omega
s=jω 得:
G
(
j
ω
)
H
(
j
ω
)
=
2
j
ω
(
1
−
j
ω
)
(
1
−
2
j
ω
)
−
ω
2
(
1
+
ω
2
)
(
1
+
4
ω
2
)
=
2
(
j
ω
+
3
ω
2
−
2
j
ω
3
)
−
ω
2
(
1
+
ω
2
)
(
1
+
4
ω
2
)
=
2
(
3
ω
2
+
ω
(
1
−
2
ω
2
)
j
)
−
ω
2
(
1
+
ω
2
)
(
1
+
4
ω
2
)
G(j\omega)H(j\omega)=\frac{2j\omega(1-j\omega)(1-2j\omega)}{-\omega^2(1+\omega^2)(1+4\omega^2)}=\frac{2(j\omega+3\omega^2-2j\omega^3)}{-\omega^2(1+\omega^2)(1+4\omega^2)}=\frac{2(3\omega^2+\omega(1-2\omega^2)j)}{-\omega^2(1+\omega^2)(1+4\omega^2)}
G(jω)H(jω)=−ω2(1+ω2)(1+4ω2)2jω(1−jω)(1−2jω)=−ω2(1+ω2)(1+4ω2)2(jω+3ω2−2jω3)=−ω2(1+ω2)(1+4ω2)2(3ω2+ω(1−2ω2)j)令
I
m
[
G
(
j
ω
)
(
j
ω
)
]
=
0
Im[G(j\omega)(j\omega)]=0
Im[G(jω)(jω)]=0 得:
ω
x
=
2
rad/s
\omega_x=\sqrt2\text{ rad/s}
ωx=2 rad/s 因此,在
ω
>
0
\omega>0
ω>0 范围内,穿过一次实轴。
可以看出,
ω
=
0
+
\omega=0^+
ω=0+ 时,
R
e
[
G
(
j
ω
)
(
j
ω
)
]
<
0
Re[G(j\omega)(j\omega)]<0
Re[G(jω)(jω)]<0,因此奈氏图草图可以画为:
(注:这是草图,能表示出相角变化,
ω
x
\omega_x
ωx, 走向等重要信息即可,不要求与原图一模一样)

有些书上草图也这样画:

用matlab写入以下程序,可以用计算机得到精准曲线:
sys = zpk([],[0 -1 -0.5],1)
nyquist(sys)

2.2 奈氏图利用
如:奈氏判据(见第四节)
2.3 关于绘制奈氏图的再探索
2.3.1 与实轴的焦点判断方法
已知 G ( s ) H ( s ) G(s)H(s) G(s)H(s),令 s = j ω s=j\omega s=jω,得到 G ( j ω ) H ( ω ) G(j\omega)H(\omega) G(jω)H(ω),然后分子分母同乘以分母的共轭,得到分母实数化的 G ( j ω ) H ( j ω ) G(j\omega)H(j\omega) G(jω)H(jω)。然后令虚部为 0 0 0,即 I m [ G ( j ω ) H ( j ω ) ] = 0 Im[G(j\omega)H(j\omega)]=0 Im[G(jω)H(jω)]=0,求解得到 ω x \omega_x ωx,然后回代,求 G ( j ω x ) H ( j ω x ) = R e [ G ( j ω x ) H ( j ω x ) ] G(j\omega_x)H(j\omega_x)=Re[G(j\omega_x)H(j\omega_x)] G(jωx)H(jωx)=Re[G(jωx)H(jωx)]即可。
相关例子已经在 2.1 节叙述,参照 2.1 节中求解 ω x = 2 r a d / s \omega_x=\sqrt 2 {\space\rm rad/s} ωx=2 rad/s 的过程。
2.3.2 起始象限的判断
例:
G
(
s
)
H
(
s
)
=
10
(
s
+
0.2
)
s
2
(
s
+
0.1
)
G(s)H(s)=\frac{10(s+0.2)}{s^2(s+0.1)}
G(s)H(s)=s2(s+0.1)10(s+0.2)绘制其开环幅频特性曲线。
解:按照 2.1 节中的解题步骤,可以求得:
G
(
j
ω
)
H
(
j
ω
)
=
10
(
j
ω
+
0.2
)
(
j
ω
)
2
(
j
ω
+
0.1
)
=
−
10
(
0.02
+
ω
2
−
0.1
j
ω
)
ω
2
(
0.01
+
ω
2
)
G(j\omega)H(j\omega)=\frac{10(j\omega+0.2)}{(j\omega)^2(j\omega+0.1)}=-\frac{10(0.02+\omega^2-0.1j\omega)}{\omega^2(0.01+\omega^2)}
G(jω)H(jω)=(jω)2(jω+0.1)10(jω+0.2)=−ω2(0.01+ω2)10(0.02+ω2−0.1jω)
ω
=
0
\omega=0
ω=0 时,
∣
G
(
0
)
H
(
0
)
∣
=
∞
|G(0)H(0)|=\infty
∣G(0)H(0)∣=∞,
∠
G
(
0
)
H
(
0
)
=
0
\angle G(0)H(0)=0
∠G(0)H(0)=0
ω
=
0
+
\omega=0^+
ω=0+ 时,
∣
G
(
0
+
)
H
(
0
+
)
∣
=
∞
|G(0^+)H(0^+)|=\infty
∣G(0+)H(0+)∣=∞,
∠
G
(
0
+
)
H
(
0
+
)
=
−
π
\angle G(0^+)H(0^+)=-\pi
∠G(0+)H(0+)=−π
ω
=
∞
\omega=\infty
ω=∞ 时,
∣
G
(
∞
)
H
(
∞
)
∣
=
0
|G(\infty)H(\infty)|=0
∣G(∞)H(∞)∣=0,
∠
G
(
∞
)
H
(
∞
)
=
−
π
\angle G(\infty)H(\infty)=-\pi
∠G(∞)H(∞)=−π
而
I
m
[
G
(
j
ω
)
H
(
j
ω
)
]
=
0.1
ω
(
0.01
+
ω
2
)
>
0
Im[G(j\omega)H(j\omega)]=\frac{0.1}{\omega(0.01+\omega^2)}>0
Im[G(jω)H(jω)]=ω(0.01+ω2)0.1>0,因此没有与实轴的交点。
那么问题来了,奈氏图应该画成下面哪种情况呢?

上图中的判定本质上是求当
ω
→
0
+
\omega\to0^+
ω→0+ 时,
I
m
[
G
(
j
0
+
)
H
(
j
0
+
)
]
Im[G(j0^+)H(j0^+)]
Im[G(j0+)H(j0+)] 的取值。于是:
lim
ω
→
0
+
I
m
[
G
(
j
ω
)
H
(
j
ω
)
]
=
lim
ω
→
0
+
0.1
ω
(
0.01
+
ω
2
)
=
+
∞
\lim_{\omega\to 0^+}{Im[G(j\omega)H(j\omega)]}=\lim_{\omega\to0^+}{\frac{0.1}{\omega(0.01+\omega^2)}}=+\infty
ω→0+limIm[G(jω)H(jω)]=ω→0+limω(0.01+ω2)0.1=+∞所以该奈氏图应当画成上图中左图的模样。
三、伯德图
3.1 开环对数频率特性曲线
伯德图是开环对数频率特性曲线,横坐标是频率的对数值,因此是十倍频等间距。实际的开环对数频率特性曲线是光滑弯曲的,我们画伯德图的时候是用直线作为渐近线去代替。
典型环节包括三部分:
(1)
K
s
ν
\frac{K}{s^\nu}
sνK 或
−
K
s
ν
-\frac{K}{s^\nu}
−sνK
(
K
>
0
)
(K>0)
(K>0)
(2)一阶环节:包括惯性环节、一阶微分环节,其交接频率
ω
=
1
T
\omega=\frac{1}{T}
ω=T1
(3)二阶环节:包括振荡环节、二阶微分环节,其交接频率
ω
=
ω
n
\omega=\omega_n
ω=ωn
3.2 绘制
- 对传递函数进行了典型环节分解,并化为尾一标准型。
- 确定各个环节交接频率和系统型别(积分环节个数,也即在原点处的极点的个数)。
- 低频段:
(1)低频段直线斜率: − 20 ν dB/dec -20\nu \text{ dB/dec} −20ν dB/dec
(2)低频段(或延长线)过定点: ( 1 , 20 lg K ) (1,20\lg{K}) (1,20lgK) - 的越过低频段后,每到一次交接频率,直线斜率变化一次,变化规则如下:
| 典型环节 | 交接频率 | 斜率变化 |
|---|---|---|
| 1 1 ± T s \frac{1}{1\pm Ts} 1±Ts1 | 1 T \frac{1}{T} T1 | -20dB/dec |
| 1 ± T s 1\pm Ts 1±Ts | 1 T \frac{1}{T} T1 | 20dB/dec |
| s 2 ω n 2 ± 2 ζ s ω n + 1 \frac{s^2}{\omega_n^2\pm2\zeta\frac{s}{\omega_n}+1} ωn2±2ζωns+1s2 | ω n \omega_n ωn | -40dB/dec |
| ω n 2 ± 2 ζ s ω n + 1 \omega_n^2\pm2\zeta\frac{s}{\omega_n}+1 ωn2±2ζωns+1 | ω n \omega_n ωn | 40dB/dec |
- 相频特性一般通过描点,然后用平滑的曲线连接的方法来描绘。
3.3 举例
已知单位负反馈系统开环传递函数: G ( s ) = 100 ( 0.1 s + 1 ) s ( 0.2 s + 1 ) ( 0.01 s + 1 ) G(s)=\frac{100(0.1s+1)}{s(0.2s+1)(0.01s+1)} G(s)=s(0.2s+1)(0.01s+1)100(0.1s+1)绘制伯德图。
解:可以看出,系统已经进行了典型环节分解,并化为了尾一标准型。
这个系统是一型系统,所以低频段斜率是 -20dB/dec。
系统增益
K
=
100
K=100
K=100,所以低频段(或延长线)过
(
1
,
20
lg
100
)
=
(
1
,
40
)
(1,20\lg100)=(1,40)
(1,20lg100)=(1,40)
交接频率 ω 1 = 1 0.2 = 5 rad/s, ω 2 = 1 0.1 = 10 rad/s, ω 3 = 1 0.01 = 100 rad/s \omega_1=\frac{1}{0.2}=5\text{ rad/s},\omega_2=\frac{1}{0.1}=10\text{ rad/s},\omega_3=\frac{1}{0.01}=100\text{ rad/s} ω1=0.21=5 rad/s,ω2=0.11=10 rad/s,ω3=0.011=100 rad/s。所以在 ω 1 \omega_1 ω1 处,对应 1 0.2 s + 1 \frac{1}{0.2s+1} 0.2s+11 斜率降低 20dB/dec;在 ω 2 \omega_2 ω2 处,对应 0.1 s + 1 0.1s+1 0.1s+1,斜率升高 20dB/dec;在 ω 3 \omega_3 ω3 处,对应 1 0.01 s + 1 \frac{1}{0.01s+1} 0.01s+11 ,斜率降低 20dB/dec
所以画出对数频率特性曲线如下:

我们用matlab试一下:
sys = zpk([-10],[0,-5,-100],100)
bode(sys)
得到结果:

3.4 谐振现象
谐振是当频率满足一定条件时,系统表现出来的一种特殊现象。比如在RLC电路中,并联谐振时,感性和容性相抵,输出信号幅值达到最大值。
对于二阶系统,谐振满足:
峰值:
M
r
=
1
2
ζ
1
−
ζ
2
(
ζ
≤
0.707
)
M_r=\frac{1}{2\zeta\sqrt{1-\zeta^2}}(\zeta\leq0.707)
Mr=2ζ1−ζ21(ζ≤0.707)
谐振频率:
ω
r
=
ω
n
1
−
2
ζ
2
\omega_r=\omega_n\sqrt{1-2\zeta^2}
ωr=ωn1−2ζ2
带宽频率:
ω
b
=
ω
n
1
−
2
ζ
2
+
2
−
4
ζ
2
+
4
ζ
4
\omega_b=\omega_n\sqrt{1-2\zeta^2+\sqrt{2-4\zeta^2+4\zeta^4}}
ωb=ωn1−2ζ2+2−4ζ2+4ζ4
截止频率:
ω
c
=
ω
n
1
+
4
ζ
4
−
2
ζ
2
\omega_c=\omega_n\sqrt{\sqrt{1+4\zeta^4}-2\zeta^2}
ωc=ωn1+4ζ4−2ζ2
相角裕度:
γ
=
arctan
2
ζ
1
+
4
ζ
4
−
2
ζ
2
\gamma=\arctan\frac{2\zeta}{\sqrt{\sqrt{1+4\zeta^4}-2\zeta^2}}
γ=arctan1+4ζ4−2ζ22ζ
超调量:
σ
%
=
e
−
π
ζ
1
−
ζ
2
×
100
%
\sigma\%=\text{e}^{-\pi\zeta\sqrt{1-\zeta^2}}\times100\%
σ%=e−πζ1−ζ2×100%
调节时间:
t
s
=
3.5
ζ
ω
n
(
Δ
=
0.05
)
t_s=\frac{3.5}{\zeta\omega_n}(\Delta=0.05)
ts=ζωn3.5(Δ=0.05)
伯德图上,如果系统在转折处出现类似这样的转折点:

说明在二阶环节处发生谐振,该点满足:
±
20
lg
2
ζ
1
−
ζ
2
=
真值
−
渐近线值
\pm20\lg{2\zeta\sqrt{1-\zeta^2}}=真值-渐近线值
±20lg2ζ1−ζ2=真值−渐近线值
如果出现:
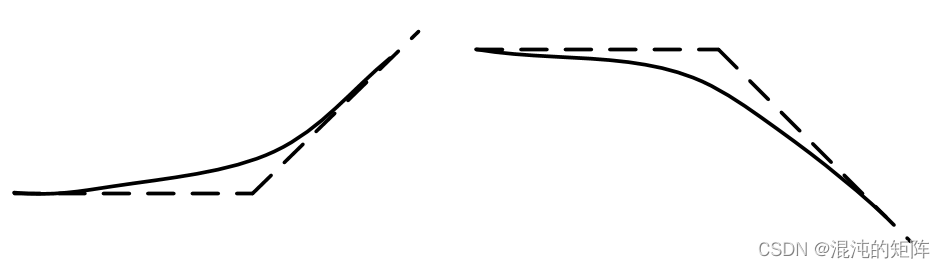
说明在一阶环节处滤波,满足:
±
20
lg
ζ
=
真值
−
渐近线值
\pm20\lg\zeta=真值-渐近线值
±20lgζ=真值−渐近线值
3.5 伯德图辨识
本质上就是画伯德图的思路反过来,从伯德图中读出转折频率,系统型别,开环增益,典型环节等信息。
- 型别:通过低频段斜率读出,低频段斜率为 − 20 ν -20\nu −20ν
- 开环增益:低频段通过(或其延长线通过) ( 1 , 20 lg K ) (1,20\lg K) (1,20lgK)
- 典型环节:通过斜率增减20还是40来判断是几阶环节
- 转折频率:通过读出转折点处的频率值,进而算出一阶环节的时间常数 T T T 或者二阶环节的固有频率 ω n \omega_n ωn
- 转折频率有时候要结合几何关系,主要是三角形的关系,比如斜边斜率、相似、勾股定理等,注意频率要取对数。
如有以下系统:

可以看出,低频段斜率为0,因此是0型系统,系统有一个一阶微分环节,四个一阶惯性环节,在一阶微分环节处,转折频率是0.1rad/s,因此时间常数是10s。低频段延长线过
(
1
,
30
)
(1,30)
(1,30),所以
20
lg
K
=
30
20\lg K=30
20lgK=30解得:
K
=
31.6
K=31.6
K=31.6
系统传递函数可以设为:
W
(
s
)
=
31.6
(
10
s
+
1
)
(
s
ω
1
+
1
)
(
s
ω
2
+
1
)
(
s
ω
3
+
1
)
(
s
ω
4
+
1
)
W(s)=\frac{31.6(10s+1)}{(\frac{s}{\omega_1}+1)(\frac{s}{\omega_2}+1)(\frac{s}{\omega_3}+1)(\frac{s}{\omega_4}+1)}
W(s)=(ω1s+1)(ω2s+1)(ω3s+1)(ω4s+1)31.6(10s+1)
然后:
{
20
=
40
−
30
lg
ω
1
−
lg
0.1
−
20
=
20
−
40
lg
ω
3
−
lg
ω
2
−
40
=
5
−
20
lg
ω
4
−
lg
ω
3
\left\{ \begin{array}{c} 20=\frac{40-30}{\lg\omega_1-\lg0.1} \\ \\ -20=\frac{20-40}{\lg\omega_3-\lg\omega_2} \\ \\ -40=\frac{5-20}{\lg\omega_4-\lg\omega_3} \\ \end{array} \right.
⎩
⎨
⎧20=lgω1−lg0.140−30−20=lgω3−lgω220−40−40=lgω4−lgω35−20
解得:
{
ω
1
=
0.316
rad/s
ω
2
=
3.48
rad/s
ω
3
=
34.8
rad/s
ω
4
=
82.6
rad/s
\left\{ \begin{array}{c} \omega_1=0.316\space \text{rad/s} \\ \\ \omega_2=3.48\space \text{rad/s} \\ \\ \omega_3=34.8\space \text{rad/s} \\ \\ \omega_4=82.6\space \text{rad/s} \\ \end{array} \right.
⎩
⎨
⎧ω1=0.316 rad/sω2=3.48 rad/sω3=34.8 rad/sω4=82.6 rad/s
∴
W
(
s
)
=
31.6
(
10
s
+
1
)
(
s
0.316
+
1
)
(
s
3.48
+
1
)
(
s
34.8
+
1
)
(
s
82.6
+
1
)
\therefore W(s)=\frac{31.6(10s+1)}{(\frac{s}{0.316}+1)(\frac{s}{3.48}+1)(\frac{s}{34.8}+1)(\frac{s}{82.6}+1)}
∴W(s)=(0.316s+1)(3.48s+1)(34.8s+1)(82.6s+1)31.6(10s+1)
四、奈氏判据
4.1 奈氏判据
- 判据: Z = P − R = P − 2 N = P − 2 ( N + − N − ) Z=P-R=P-2N=P-2(N_+-N_-) Z=P−R=P−2N=P−2(N+−N−)
- 稳定条件: Z = 0 ⇔ P = 2 ( N + − N − ) Z=0\Leftrightarrow P=2(N_+-N_-) Z=0⇔P=2(N+−N−)
- P P P:开环传递函数具有正实部的极点数
- R R R:奈奎斯特图中,半闭合曲线 Γ G H \Gamma_{GH} ΓGH(2.1中实线) 包围原点的圈数。
- N N N:奈氏图中半闭合曲线 Γ G H \Gamma_{GH} ΓGH 穿越 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点左侧实轴的次数。
- N + N_+ N+: ( − 1 , j 0 ) (-1,j0) (−1,j0) 点左侧,正穿越次数,即半闭合曲线从上往下穿过实轴的次数。
- N − N_- N−: ( − 1 , j 0 ) (-1,j0) (−1,j0) 点左侧,负穿越次数,即半闭合曲线从下往上穿过实轴的次数。
4.2 正穿越和负穿越

上图展示的几个情况中:
(1)图1:交点在
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 点左侧,顺时针运行,所以负穿越1次,
N
−
=
1
,
N
+
=
0
N_-=1,N_+=0
N−=1,N+=0
(2)图2:交点在
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 点右侧,从下到上顺时针运行,所以没有在
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 左侧的交点,因此正负穿越次数都记 0
(3)图3:三个交点,两个在
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 左侧,一个在右侧,从左向右运行,所以正负穿越各一次,
N
−
=
N
+
=
1
N_-=N_+=1
N−=N+=1
(4)图4:两个交点,都在
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 左侧,顺时针运行,但一个交点停止于实轴,所以负穿越次数为1,正穿越次数为0.5,即
N
−
=
1
,
N
+
=
0.5
N_-=1,N_+=0.5
N−=1,N+=0.5
五、稳定裕度
5.1 相角裕度
5.1.1 定义
设 ω c \omega_c ωc 为系统的截止频率,则 A ( ω c ) = ∣ G ( j ω c ) H ( j ω c ) ∣ = 1 A(\omega_c)=|G(j\omega_c)H(j\omega_c)|=1 A(ωc)=∣G(jωc)H(jωc)∣=1,定义相角裕度: γ = π + ∠ G ( j ω c ) H ( j ω c ) \gamma=\pi+\angle G(j\omega_c)H(j\omega_c) γ=π+∠G(jωc)H(jωc)
5.1.2 相角裕度的频率特性意义
相角裕度的含义是:对于闭环稳定系统,如果开环相频特性再滞后 γ \gamma γ,则系统将处于临界稳定。
5.1.3 计算相角裕度
- 令 ∣ G ( j ω c ) H ( ω c ) ∣ = 1 |G(j\omega_c)H(\omega_c)|=1 ∣G(jωc)H(ωc)∣=1 求截止频率 ω c \omega_c ωc
- γ = π + ∠ G ( j ω c ) H ( j ω c ) \gamma=\pi+\angle G(j\omega_c)H(j\omega_c) γ=π+∠G(jωc)H(jωc)
5.2 幅值裕度
5.2.1 定义
设
ω
x
\omega_x
ωx 为系统穿越频率,则幅值裕度定义为:
h
=
1
/
∣
G
(
j
ω
x
)
H
(
j
ω
x
)
∣
h=1/|G(j\omega_x)H(j\omega_x)|
h=1/∣G(jωx)H(jωx)∣
对数坐标下,也定义为:
h
(
dB
)
=
−
20
lg
∣
G
(
j
ω
x
)
H
(
j
ω
x
)
∣
h(\text {dB})=-20\lg|G(j\omega_x)H(j\omega_x)|
h(dB)=−20lg∣G(jωx)H(jωx)∣
5.2.2 幅值裕度的频率特性意义
幅值裕度的含义是:对于闭环稳定系统,如果开环幅频特性再增大 h h h 倍,则系统将处于临界稳定。
用一张图说明幅值裕度和相角裕度的意义。

5.2.3 计算幅值裕度
- 令 ∠ G ( j ω c ) H ( ω c ) = ( 2 k + 1 ) π \angle G(j\omega_c)H(\omega_c)=(2k+1)\pi ∠G(jωc)H(ωc)=(2k+1)π 求穿越频率 ω x \omega_x ωx
- h = 1 / ∣ G ( j ω x ) H ( j ω x ) ∣ h=1/|G(j\omega_x)H(j\omega_x)| h=1/∣G(jωx)H(jωx)∣

























 326
326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








