[ToolsChains CPP] Osqp库的基础&&示例&&MPCdemo

最新推荐文章于 2024-05-23 16:42:37 发布
最新推荐文章于 2024-05-23 16:42:37 发布
阅读量1.8k 收藏 19
点赞数 21
分类专栏： 工具链 cpp python 使用笔记 Autonomous Driving Algorithm 文章标签： 自动驾驶 c++ linux ubuntu 学习 最小二乘法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_46479223/article/details/135070489
版权

写在前面

本文参考官方教程，重复经典示例，然后自行搭建一个MPC控制器，并且接入我的闭环仿真器。

outline

  • osqp （c语言处理稀疏矩阵的表现形式太难受了 - 建议不用python matlab的话 入门即放弃，）
  • osqp eigen （于是学习使用了osqp-eigen版）
  • MPC 算法构建

安装

参考https://osqp.org/docs/get_started/sources.html进行安装，

关于安装的路径，如果是源代码安装的可以直接看编译文件cmake或者比编译时候的显示找到路径，如果是命令行安装的可以使用命令行来查找。
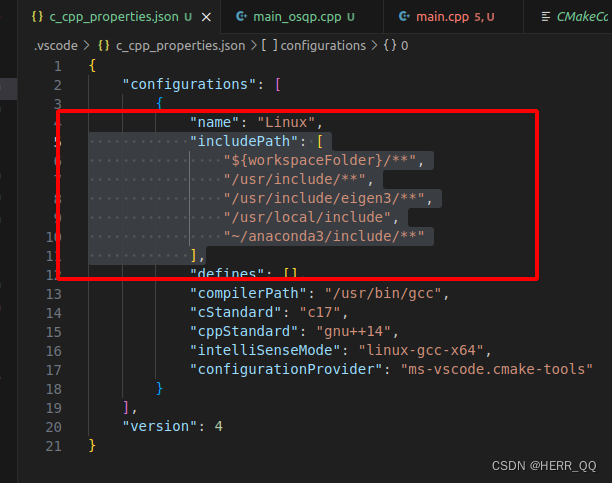在这里插入图片描述我用来源码编译然后install安装、命令行安装、conda安装的方式。基本以上路径可以覆盖。

观察系统安装路径，安装的目标在include中嵌套了一层文件夹，所以带上了路径#include “osqp/osqp.h”
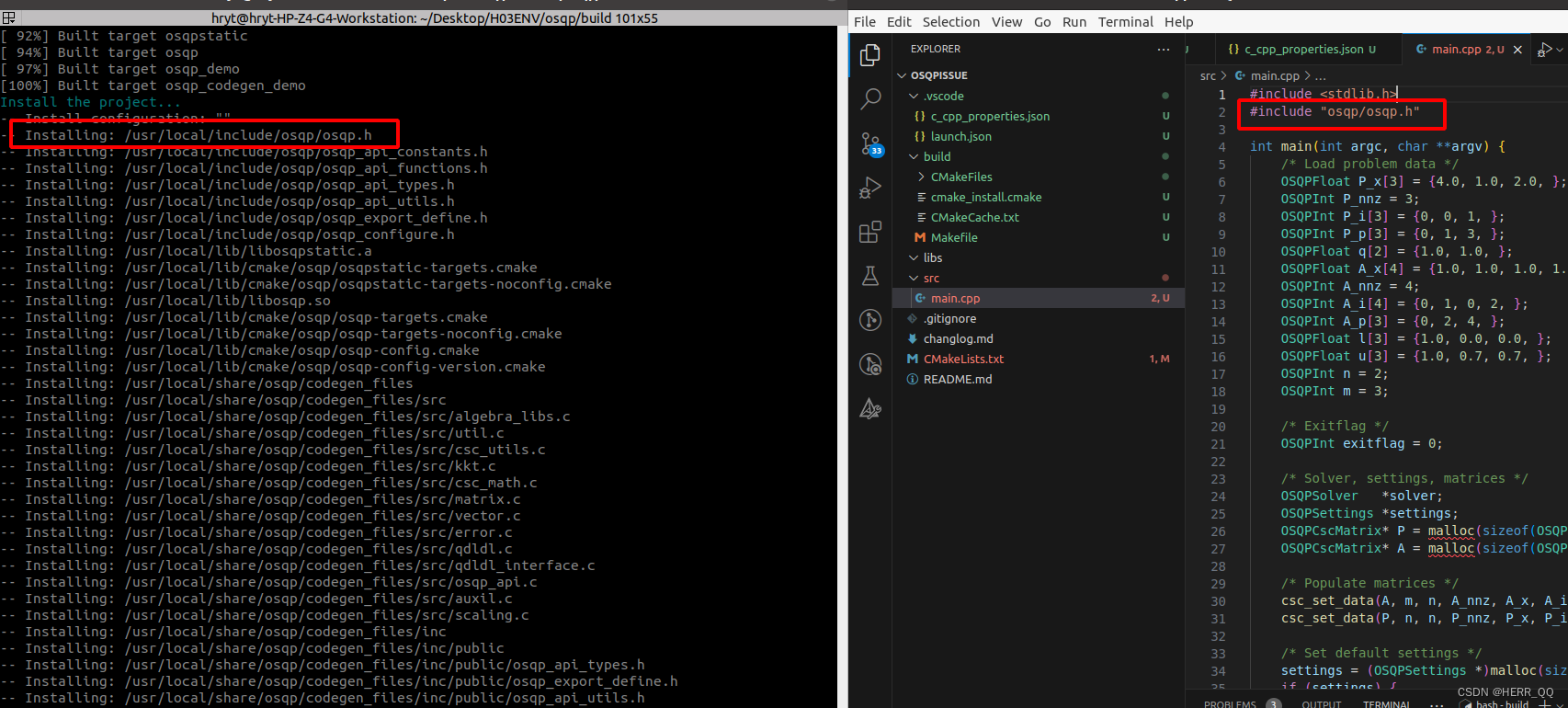
在这里插入图片描述

官网案例实现（CPP）：

https://osqp.org/docs/examples/index.html

  • 源代码是基于c ，由于我的cmakelist设置等问题，我把部分c语言的东西换成立cpp来实现的
  • c语言处理稀疏矩阵的表现形式太难受了，于是我只实现了最简单的例子，而后使用了osqp-eigen版
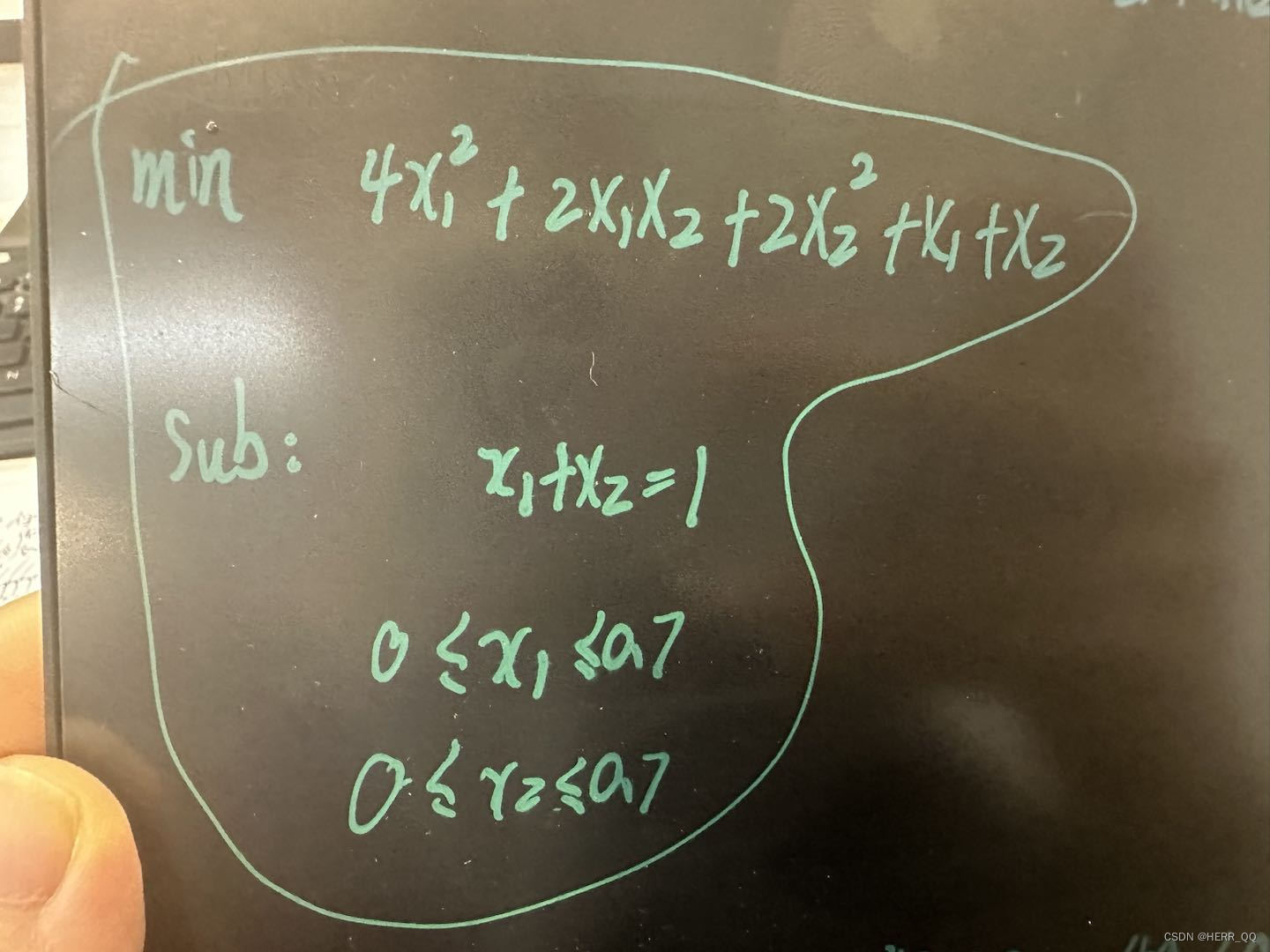
    在这里插入图片描述

osqp代码如下：

#include <stdlib.h>
#include "osqp/osqp.h"
#include <string>

int main(int argc, char **argv) {
    /* Load problem data */
    OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };
    OSQPInt P_nnz = 3;
    OSQPInt P_i[3] = {0, 0, 1, };
    OSQPInt P_p[3] = {0, 1, 3, };
    OSQPFloat q[2] = {1.0, 1.0, };
    OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };
    OSQPInt A_nnz = 4;
    OSQPInt A_i[4] = {0, 1, 0, 2, };
    OSQPInt A_p[3] = {0, 2, 4, };
    OSQPFloat l[3] = {1.0, 0.0, 0.0, };
    OSQPFloat u[3] = {1.0, 0.7, 0.7, };
    OSQPInt n = 2;
    OSQPInt m = 3;



    // P_x[3]： 这是矩阵 P 的非零元素的数组。在这个例子中，P 是一个 2x2 的对称矩阵，由于是对称的，只需要存储上三角或下三角的元素。这里 {4.0, 1.0, 2.0} 表示的是上三角的元素。

    // P_nnz： 这是矩阵 P 的非零元素的数量。在这个例子中，P_nnz 等于 3。

    // P_i[3]： 这是矩阵 P 的非零元素的行索引数组。对应于 P_x 中的每个非零元素，P_i 存储其行索引。在这里，{0, 0, 1} 表示 {4.0, 1.0, 2.0} 对应的行索引。

    // P_p[3]： 这是矩阵 P 的列指针数组。它指示每一列的起始位置在 P_x 和 P_i 数组中的索引。在这个例子中，{0, 1, 3} 表示第一列从索引 0 开始，第二列从索引 1 开始，第三列从索引 3 开始。qkf：也就是还原行与列

    // q[2]： 这是目标函数的线性项。在这个例子中，目标函数是一个二次函数，q 中存储的是线性项的系数。

    // A_x[4]： 这是约束矩阵 A 的非零元素的数组。在这个例子中，A_x 存储了矩阵 A 的所有非零元素，即 {1.0, 1.0, 1.0, 1.0}。

    // A_nnz： 这是矩阵 A 的非零元素的数量。在这个例子中，A_nnz 等于 4。

    // A_i[4]： 这是矩阵 A 的非零元素的行索引数组。对应于 A_x 中的每个非零元素，A_i 存储其行索引。在这里，{0, 1, 0, 2} 表示 {1.0, 1.0, 1.0, 1.0} 对应的行索引。

    // A_p[3]： 这是矩阵 A 的列指针数组，指示每一列的起始位置在 A_x 和 A_i 数组中的索引。

    // l[3]： 这是约束的下界。在这个例子中，l 存储了每个约束的下界，即 {1.0, 0.0, 0.0}。

    // u[3]： 这是约束的上界。在这个例子中，u 存储了每个约束的上界，即 {1.0, 0.7, 0.7}。

    // n： 问题的变量数，也就是优化问题中的变量维度。在这个例子中，n 等于 2。

    // m： 问题的约束数。在这个例子中，m 等于 3。


    /* Exitflag */
    OSQPInt exitflag = 0;

    /* Solver, settings, matrices */
    OSQPSolver   *solver;
    OSQPSettings *settings;
    OSQPCscMatrix* P = static_cast<OSQPCscMatrix*>(std::malloc(sizeof(OSQPCscMatrix)));
    OSQPCscMatrix* A = static_cast<OSQPCscMatrix*>(std::malloc(sizeof(OSQPCscMatrix)));

    /* Populate matrices */
    csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);
    csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);

    /* Set default settings */
    settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));
    if (settings) {
        osqp_set_default_settings(settings);
        settings->alpha = 1.0; /* Change alpha parameter */
    }

    /* Setup solver */
    exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);

    /* Solve problem */
    if (!exitflag) exitflag = osqp_solve(solver);

    /* Cleanup */
    osqp_cleanup(solver);
    if (A) std::free(A);
    if (P) std::free(P);
    if (settings) free(settings);

    return (int)exitflag;
};

运行结果
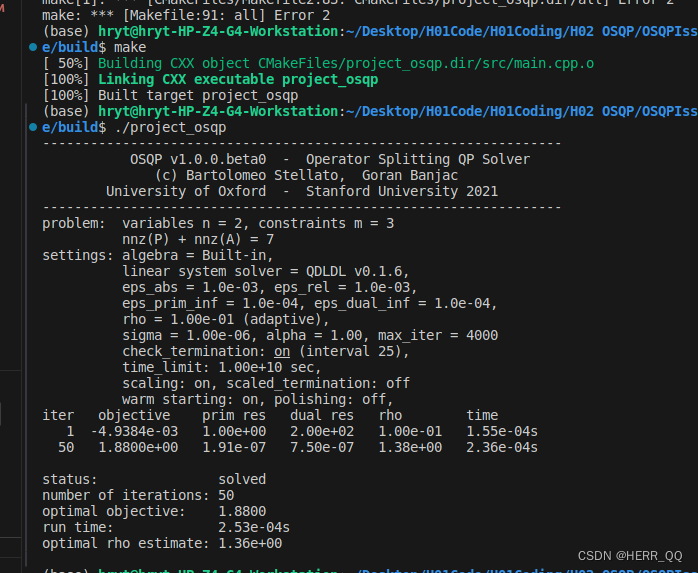在这里插入图片描述关于输出结果的解释我询问了gpt：

GPT A：
这是OSQP求解一个凸二次规划问题的输出结果。以下是对输出的解读：
问题规模和结构

变量数目：n = 2
约束数目：m = 3
非零元素数目：nnz(P) + nnz(A) = 7

OSQP设置

代数法：Built-in
线性系统求解器：QDLDL v0.1.6
终止准则：
    相对绝对误差：eps_abs = 1.0e-03
    相对相对误差：eps_rel = 1.0e-03
    主变量无穷范数误差：eps_prim_inf = 1.0e-04
    对偶变量无穷范数误差：eps_dual_inf = 1.0e-04
内点方法参数：
    rho (亲和力参数)：1.00e-01（自适应）
    sigma：1.00e-06
    alpha：1.00
    最大迭代次数：max_iter = 4000
    终止检查：每25次迭代检查一次
    时间限制：1.00e+10秒（相当于没有时间限制）
    缩放：开启
    缩放终止检查：关闭
其他设置：
    热启动：开启
    精炼：关闭

求解过程

第一次迭代：
    目标函数值：-4.9384e-03
    主变量（原始变量）相对误差：1.00e+00
    对偶变量相对误差：2.00e+02
    亲和力参数：1.00e-01（自适应）
    时间：1.55e-04秒

第50次迭代：
    目标函数值：1.8800e+00
    主变量相对误差：1.91e-07
    对偶变量相对误差：7.50e-07
    亲和力参数：1.38e+00
    时间：2.36e-04秒

最终结果

状态：已解决
迭代次数：50
最优目标值：1.8800
运行时间：2.53e-04秒
最优亲和力参数估计：1.36e+00

我继续追问：

Q：osqp不是应该求解最小值吗，为什么目标函数值还变大了

GPT A：
你提出的疑问是非常合理的。在一般情况下，确实期望优化算法（尤其是求解凸优化问题的算法）的目标函数值随着迭代逐渐减小，因为算法的目标是找到一个能够使目标函数值最小化的解。

然而，有时在实际应用中，目标函数值的变化可能受到问题本身的特性、算法的内部细节或者算法参数的影响。在你提供的输出中，可能是由于算法初始化的原因，首次迭代的目标函数值为负值，而之后的迭代过程中逐渐增加并最终趋于正值。

有几个可能的原因：

算法初始化： 初始点的选择可能导致了首次迭代的目标函数值为负。这通常不影响最终的优化结果，因为目标是在迭代中找到更好的解。

数值精度： 在计算中，特别是在数值优化中，数值精度的影响可能导致目标函数值的轻微波动。这些波动通常在优化过程中逐渐减小。

亲和力参数的调整： 亲和力参数（rho）的自适应调整可能导致目标函数值的变化。这是因为亲和力参数的调整可能会影响算法在原始问题和对偶问题之间的权衡。

虽然首次迭代的目标函数值为负可能看起来有点奇怪，但关键是最终算法是否收敛到了满足准确性要求的解。在你提供的输出中，算法的最终状态是 “已解决”，迭代次数也是有限的，最终目标函数值是正的，这可能表示算法在问题上取得了满意的结果。

osqp eigen

官网教学：https://robotology.github.io/osqp-eigen/
案例教学：https://blog.csdn.net/shoufei403/article/details/108672152
案例教学2：https://zhuanlan.zhihu.com/p/376122376

推荐用conda方式安装
在这里插入图片描述

示例代码

以下代码是根据链接教程中我补全的代码，教程中仅为片段

#include <stdlib.h>
#include "osqp/osqp.h"
#include "OsqpEigen/OsqpEigen.h"
#include <Eigen/Dense>
#include <iostream>

int main(int argc, char **argv) {
    Eigen::SparseMatrix<double> hessian;
    Eigen::VectorXd gradient;
    Eigen::SparseMatrix<double> linearMatrix;
    Eigen::VectorXd lowerBound;
    Eigen::VectorXd upperBound;

    short int num_var=2,num_contrains=3;
    hessian.resize(num_var,num_var);
    hessian.insert(0,0) = 1;
    hessian.insert(1,0) = -1;
    hessian.insert(0,1) = -1;
    hessian.insert(1,1) = 2;
    std::cout << "hessian:" << std::endl << hessian << std::endl;
    gradient.resize(2);
    gradient << -2, -6;
    std::cout << "gradient:" << std::endl << gradient << std::endl;
    linearMatrix.resize(3,2);
    linearMatrix.insert(0,0) = 1;
    linearMatrix.insert(0,1) = 1;
    linearMatrix.insert(1,0) = -1;
    linearMatrix.insert(1,1) = 2;
    linearMatrix.insert(2,0) = 2;
    linearMatrix.insert(2,1) = 1;
    std::cout << "linearMatrix:" << std::endl << linearMatrix << std::endl;

    lowerBound.resize(3);
    lowerBound << -OsqpEigen::INFTY, -OsqpEigen::INFTY, -OsqpEigen::INFTY;
    std::cout << "lowerBound:" << std::endl << lowerBound << std::endl;

    upperBound.resize(3);
    upperBound << 2, 2, 3;
    std::cout << "upperBound:" << std::endl << upperBound << std::endl;

    OsqpEigen::Solver solver;

    solver.settings()->setWarmStart(true);

    solver.data()->setNumberOfVariables(num_var); //设置A矩阵的列数，即n
    solver.data()->setNumberOfConstraints(num_contrains); //设置A矩阵的行数，即m
    if(!solver.data()->setHessianMatrix(hessian)) return 1;//设置P矩阵
    if(!solver.data()->setGradient(gradient)) return 1; //设置q or f矩阵。当没有时设置为全0向量
    if(!solver.data()->setLinearConstraintsMatrix(linearMatrix)) return 1;//设置线性约束的A矩阵
    if(!solver.data()->setLowerBound(lowerBound)) return 1;//设置下边界
    if(!solver.data()->setUpperBound(upperBound)) return 1;//设置上边界

    if (!solver.initSolver()) return 1;

    if (!solver.solve()) return 1;

    auto QPSolution=solver.getSolution();
    std::cout <<"size of QP solution： " << QPSolution.size()<<std::endl;
    std::cout << "Solution for x[0]: " << QPSolution(0) << std::endl;
    std::cout << "Solution for x[1]: " << QPSolution(1) << std::endl;




};

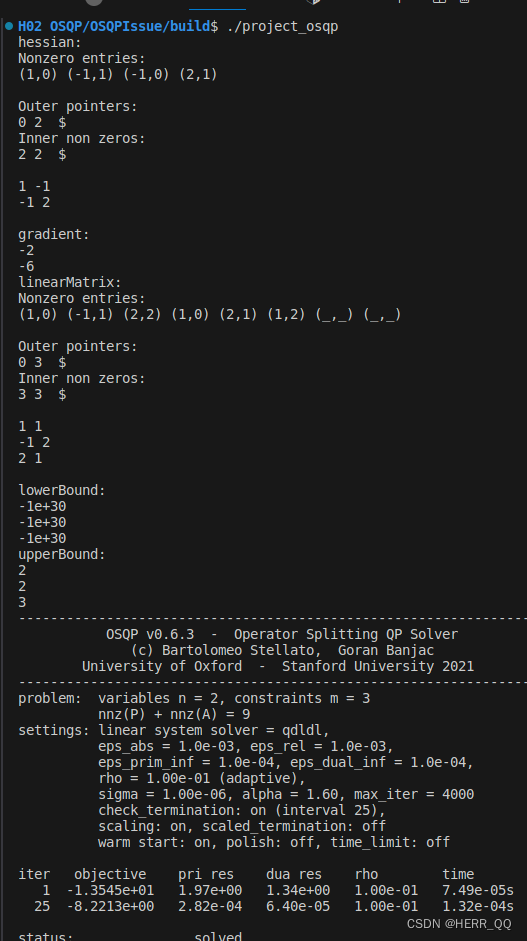
在这里插入图片描述

以下为答案
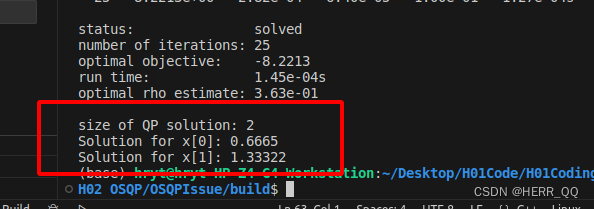
在这里插入图片描述
关于例子中的其他两种问题：等式、边界、甚至比如不等式约束，在这个框架下改变很小，不再详细写出。

MPC 算法构建 下一次更新

HERR_QQ
关注
  • 21
    点赞
  • 踩
  • 19
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
【规划】Apollo QSQP接口详解
zyntj1992的博客
08-21 3424
Apollo OSQP接口详解 Created by Lemon Date: 17/6/2021 参考资料： https://zhuanlan.zhihu.com/p/325645742 1. OSQP简介 OSQP是一个凸二次规划问题的求解器，其解决的问题形如： KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ &minimize \qqu… 其中xxx是需要优化的变量，且
pyMPC:基于OSQP求解器的模型预测控制（MPC）Python库
05-04
pyMPC Python中的线性约束模型预测控制（MPC）： 在哪里 要求 pyMPC需要以下软件包： 麻木 科学的 matplotlib 安装 获取pyMPC项目的本地副本。 例如，运行 git clone https://github.com/forgi86/pyMPC.git 在终端中使用git克隆项目。 或者，从此下载压缩的pyMPC项目并将其解压缩到本地文件夹中 通过运行安装pyMPC pip install -e . 在pyMPC项目根文件夹中（文件setup.py所在的位置）。 支持平台 我们在以下平台上成功测试了pyMPC： 具有x86-64 CPU的PC上的Windows 10 具有x86-64 CPU的PC上的Ubuntu 18.04 LTS Raspbian PI 3 rev B上的Raspbian Buster 有关Raspberry PI平台的详
【OSQP】MPC代码学习与部署
qq_44768318的博客
07-27 861
u的最大值最小值约束一个osqp实例需要参数PqAlu分别对应目标函数中的二次型矩阵线性矩阵，关于决策变量的线性约束Alu。
#include ＜osqp.h＞ osqp.h文件不存在
最新发布
qq_37087723的博客
05-23 102
解决方法，将osqp目录复制到/usr/local/include目录下。
C++中求解二次规划问题（OSQP）的一个使用实例
chaser30的博客
04-19 3263
库的安装（eigen/OSQP/OSQP-eigen）及其他实例可以参考这个链接。，其中常数项对二次型求解没有影响，可以直接忽略。由于二次规划问题求解器默认的求解形式为。以下面的一个优化问题求解为例。Cmakelist文件如下。
OSQP文档学习
BigDavid123的博客
02-19 1643
osqp求解器官方文档学习
二次规划（QP）与OSQP求解器
牛仔很忙
04-18 1万+
优化在很多领域都发挥着重要应用，其中自动驾驶的运动规划可以看做一个优化问题，根据实际情况进行合理简化和建模。 一个优化问题包含：优化目标和约束条件（包含等式约束、不等式约束）。 如果约束条件或目标函数包含非线性，则为非线性优化。二次规划是一种特殊的非线性规划，也是标准的凸优化问题，能够快速求解。 在路径/轨迹优化中经常建模为二次优化问题进行求解，很多MPC的求解过程也是转化为序列二次规划进行求解。 二次优化的标准形式为： 关于二次项系数的正定性，以及优化理论的剖析，此处暂不做探讨，可以阅读...
使用OSQP解决二次凸优化(QP)问题
热门推荐
shoufei403的博客
09-19 2万+
什么是二次规划问题 如何构造二次规划问题 如何解二次规划问题
OSQP二次规划求解库使用说明
davidhopper的博客
05-10 2388
例如：P_p = {0, 1, 3}表示：1 - 0 = 1 代表矩阵P第一列元素非零个数为１个，3 - 1 = 2 代表矩阵P第二列元素非零个数为２个。中非零元素行索引为：0, 0, 1，这是按照先第一列，再第二列。第二列的非零元素为1, 2，行索引分别为：0, 1，于是记为：P_i = {0, 0, 1}；中第一列非零元素是1个，第二列非零元素是2个，记为：P_p = {0, 1, 3}。的元素全部为实数，因此它一定是对称矩阵。中非零元素为：4, 1, 2，记为：P_x = {4, 1, 2}；
OSQP求解凸优化问题的步骤及实例
肥嘟嘟的左卫门
01-11 3566
OSQP是一种求解QP问题的数值优化软件，以下简单介绍OSQP软件的使用方法 一、 概述 首先是凸优化问题的定义以及两种典型的特例（线性规划与二次规划），如下图所示。 这里不介绍QP问题的拓展形式如SOCP等 OSQP软件的核心是ADMM算法 Ø交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）是一种求解优化问题的计算框架, 适用于求解分布式凸优化问题 如果仅仅是简单的使用，不需要了解ADMM算法，但是如果调试OSQP软件的参数，就需要深入
yaml-cpp库的编译&安装
01-20
**yaml-cpp库的编译与安装指南** yaml-cpp是一个用C++编写的YAML解析器和生成器库，广泛应用于配置文件处理和数据序列化。为了在项目中使用yaml-cpp，我们需要先下载、解压源代码，然后进行编译和安装。以下是一...
[ToolsChains CPP] Osqp的使用之二：MPCdemo
12-20
[ToolsChains CPP] Osqp的使用之二：MPCdemo
CSharp~CPP.rar_c# .cpp_c#与c++_cpp参数表 &
09-23
C++与C#参数对照表C++与C#参数对照表C++与C#参数对照表C++与C#参数对照表
Cpp:C++ 作品&家庭作业
07-08
Cppo欧阳易紫o 的C艹作业源码~！以后就都存放在这里了~偶尔看心情写一写注释~╮(╯3╰)╭
C语言中&&的使用.cpp
05-15
初学者C语言
LQR、MPC以及osqp库
抗魔斗篷
12-13 2909
最优控制是指在给定的约束条件下，寻求一个控制，使给定的系统性能指标达到极大值(或极小值)。
二次规划及osqp使用
m0_50851031的博客
05-07 422
minimize 1/2xTHx+Gxsubject lb≤Ax ≤ ub minimize \ 1/2x^THx + Gx\\ subject\ lb\leq Ax\ \leq\ ub minimize 1/2xTHx+Gxsubject lb≤Ax ≤ ubf(x)=1/2x12+x22−x1x2−2x1−6x2x1+x2≤2−x1+2x2≤22x1+x2≤3 f(x) = 1/2x_1^2+x_2^2-x_1x_2-2x_1-6x_2\\ x_1+x_2\leq2\\ -x_1+2x_2\leq2\\
探索OSQP：一个高效优化求解器的奥秘
gitblog_00015的博客
03-25 407
探索OSQP：一个高效优化求解器的奥秘 项目地址:https://gitcode.com/oxfordcontrol/osqp OSQP是一个开源的二次规划（Quadratic Programming,QP）求解器，由牛津大学控制工程实验室开发并维护。该项目旨在提供一种快速、可靠的解决方案，以处理大规模线性优化问题。本文将深入探讨OSQP的技术特性，应用场景及其为何值得广大开发者和研究人员尝试。 ...
Apollo中osqp库的使用
weixin_46604884的博客
08-21 1118
【代码】Apollo中osqp库的使用。
"cd \"/users/tanzexing/desktop/cpp/\" && gcc tempcoderunnerfile.c -o tempcoderu"
09-21
这段命令是用于在计算机中操作文件路径的指令。在这个例子中，cd表示“change directory”，也就是“改变目录”的意思。后面的参数"/users/tanzexing/desktop/cpp/"表示要改变的目录路径。具体解释如下： cd：这是一个命令，用于告诉计算机即将进行的操作。 "/users/tanzexing/desktop/cpp/"：这是文件路径，具体包括了一系列目录和文件夹名称。其中： - /users：表示根目录下的users文件夹。 - /tanzexing：表示在users文件夹中的tanzexing文件夹。 - /desktop：表示在tanzexing文件夹中的desktop文件夹。 - /cpp：表示在desktop文件夹中的cpp文件夹。 整个命令的目的是将当前的工作目录改变为"/users/tanzexing/desktop/cpp/"所指定的路径。也就是说，命令执行后，可以在"/users/tanzexing/desktop/cpp/"下进行后续操作，如编译cpp程序、创建文件等。 需要注意的是，具体路径的格式可能会根据操作系统的不同有所差别，这里给出的解释是基于常见的Unix/Linux系统。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值