矩阵计算
参考链接:矩阵如何运算?——线性代数_矩阵计算-CSDN博客
矩阵计算:【前找行,后找列,相乘相加】。
行列式计算
参考链接:实用的行列式计算方法 —— 线性代数(det)_det线性代数-CSDN博客
参考链接:行列式的计算方法(含四种,看完就会!)-CSDN博客
一、对角线法
▍以三阶行列式为例:

①将第一、二列平移到行列式右侧
②如图做出六条斜对角线
③对角线上的元素相乘,红色相加的和 减去 蓝色相加的和

D3=
对角线法也是三阶行列式计算使用最广泛的方法
▍ 对角线法适用于二、三阶行列式,对于更高阶的行列式暂时未找到规律
二、代数余子式法
三、等价转化法
四、逆序数法
四种行列式的计算方法:
▍其中对角线法,是使用最简单、最广泛的方法
▍代数余子式法和等价转化法,在特定情况下能极大程度上简便运算,但需要读者对行列式进行灵活地观察
▍逆序数法,是一种更加基础的方法,使用起来比较复杂
数学符号及读法大全 & 数学运算符号及含义
参考链接:【高数】数学符号及读法大全and数学运算符号及含义_高数符号大全及意义-CSDN博客
数学符号及读法大全,并解释了运算符号含义。
| 大写 | 小写 | 英文注音 | 国际音标 | 中文注音 |
| Α | α | alpha | alfa | 阿耳法 |
| Β | β | beta | beta | 贝塔 |
| Γ | γ | gamma | gamma | 伽马 |
| Δ | δ | deta | delta | 德耳塔 |
| Ε | ε | epsilon | epsilon | 艾普西隆 |
| Ζ | ζ | zeta | zeta | 截塔 |
| Η | η | eta | eta | 艾塔 |
| Θ | θ | theta | θita | 西塔 |
| Ι | ι | iota | iota | 约塔 |
| Κ | κ | kappa | kappa | 卡帕 |
| ∧ | λ | lambda | lambda | 兰姆达 |
| Μ | μ | mu | miu | 缪 |
| Ν | ν | nu | niu | 纽 |
| Ξ | ξ | xi | ksi | 可塞 |
| Ο | ο | omicron | omikron | 奥密可戎 |
| ∏ | π | pi | pai | 派 |
| Ρ | ρ | rho | rou | 柔 |
| ∑ | σ | sigma | sigma | 西格马 |
| Τ | τ | tau | tau | 套 |
| Υ | υ | upsilon | jupsilon | 衣普西隆 |
| Φ | φ | phi | fai | 斐 |
| Χ | χ | chi | khai | 喜 |
| Ψ | ψ | psi | psai | 普西 |
| Ω | ω | omega | omiga | 欧米噶 |
| 符号 | 含义 |
| i | -1的平方根 |
| f(x) | 函数f在自变量x处的值 |
| sin(x) | 在自变量x处的正弦函数值 |
| exp(x) | 在自变量x处的指数函数值,常被写作ex |
| a^x | a的x次方;有理数x由反函数定义 |
| ln x | exp x 的反函数 |
| ax | 同 a^x |
| logba | 以b为底a的对数;blogba = a |
| cos x | 在自变量x处余弦函数的值 |
| tan x | 其值等于 sin x/cos x |
| cot x | 余切函数的值或 cos x/sin x |
| sec x | 正割含数的值,其值等于 1/cos x |
| csc x | 余割函数的值,其值等于 1/sin x |
| asin x | y,正弦函数反函数在x处的值,即 x = sin y |
| acos x | y,余弦函数反函数在x处的值,即 x = cos y |
| atan x | y,正切函数反函数在x处的值,即 x = tan y |
| acot x | y,余切函数反函数在x处的值,即 x = cot y |
| asec x | y,正割函数反函数在x处的值,即 x = sec y |
| acsc x | y,余割函数反函数在x处的值,即 x = csc y |
| θ | 角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时 |
| i, j, k | 分别表示x、y、z方向上的单位向量 |
| (a, b, c) | 以a、b、c为元素的向量 |
| (a, b) | 以a、b为元素的向量 |
| (a, b) | a、b向量的点积 |
| a•b | a、b向量的点积 |
| (a•b) | a、b向量的点积 |
| |v| | 向量v的模 |
| |x| | 数x的绝对值 |
| Σ | 表示求和,通常是某项指数。下边界值写在其下部,上边界值写在其上部。如j从1到100 的和可以表示成:。这表示 1 + 2 + … + n |
| M | 表示一个矩阵或数列或其它 |
| |v> | 列向量,即元素被写成列或可被看成k×1阶矩阵的向量 |
| <v| | 被写成行或可被看成从1×k阶矩阵的向量 |
| dx | 变量x的一个无穷小变化,dy, dz, dr等类似 |
| ds | 长度的微小变化 |
| ρ | 变量 (x2 + y2 + z2)1/2 或球面坐标系中到原点的距离 |
| r | 变量 (x2 + y2)1/2 或三维空间或极坐标中到z轴的距离 |
| |M| | 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积 |
| ||M|| | 矩阵M的行列式的值,为一个面积、体积或超体积 |
| det M | M的行列式 |
| M-1 | 矩阵M的逆矩阵 |
| v×w | 向量v和w的向量积或叉积 |
| θvw | 向量v和w之间的夹角 |
| A•B×C | 标量三重积,以A、B、C为列的矩阵的行列式 |
| uw | 在向量w方向上的单位向量,即 w/|w| |
| df | 函数f的微小变化,足够小以至适合于所有相关函数的线性近似 |
| df/dx | f关于x的导数,同时也是f的线性近似斜率 |
| f ' | 函数f关于相应自变量的导数,自变量通常为x |
| ∂f/∂x | y、z固定时f关于x的偏导数。通常f关于某变量q的偏导数为当其它几个变量固定时df 与dq的比值。任何可能导致变量混淆的地方都应明确地表述 |
| (∂f/∂x)|r,z | 保持r和z不变时,f关于x的偏导数 |
| grad f | 元素分别为f关于x、y、z偏导数 [(∂f/∂x), (∂f/∂y), (∂f/∂z)] 或 (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k; 的向量场,称为f的梯度 |
| ∇ | 向量算子(∂/∂x)i + (∂/∂x)j + (∂/∂x)k, 读作 "del" |
| ∇f | f的梯度;它和 uw 的点积为f在w方向上的方向导数 |
| ∇•w | 向量场w的散度,为向量算子∇ 同向量 w的点积, 或 (∂wx /∂x) + (∂wy /∂y) + (∂wz /∂z) |
| curl w | 向量算子 ∇ 同向量 w 的叉积 |
| ∇×w | w的旋度,其元素为[(∂fz /∂y) - (∂fy /∂z), (∂fx /∂z) - (∂fz /∂x), (∂fy /∂x) - (∂fx /∂y)] |
| ∇•∇ | 拉普拉斯微分算子:(∂2/∂x2) + (∂/∂y2) + (∂/∂z2) |
| f "(x) | f关于x的二阶导数,f '(x)的导数 |
| d2f/dx2 | f关于x的二阶导数 |
| f(2)(x) | 同样也是f关于x的二阶导数 |
| f(k)(x) | f关于x的第k阶导数,f(k-1) (x)的导数 |
| T | 曲线切线方向上的单位向量,如果曲线可以描述成 r(t), 则T = (dr/dt)/|dr/dt| |
| ds | 沿曲线方向距离的导数 |
| κ | 曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds| |
| N | dT/ds投影方向单位向量,垂直于T |
| B | 平面T和N的单位法向量,即曲率的平面 |
| τ | 曲线的扭率:|dB/ds| |
| g | 重力常数 |
| F | 力学中力的标准符号 |
| k | 弹簧的弹簧常数 |
| pi | 第i个物体的动量 |
| H | 物理系统的哈密尔敦函数,即位置和动量表示的能量 |
| {Q, H} | Q, H的泊松括号 |
| 以一个关于x的函数的形式表达的f(x)的积分 | |
| 函数f 从a到b的定积分。当f是正的且 a < b 时表示由x轴和直线y = a, y = b 及在这些直线之间的函数曲线所围起来图形的面积 | |
| L(d) | 相等子区间大小为d,每个子区间左端点的值为 f的黎曼和 |
| R(d) | 相等子区间大小为d,每个子区间右端点的值为 f的黎曼和 |
| M(d) | 相等子区间大小为d,每个子区间上的最大值为 f的黎曼和 |
| m(d) | 相等子区间大小为d,每个子区间上的最小值为 f的黎曼和 |
公式输入符号 :
+: plus(positive正的)
-: minus(negative负的)
*: multiplied by
÷: divided by
=: be equal to
≈: be approximately equal to
(): round brackets(parenthess)
[]: square brackets
{}: braces
∵: because
∴: therefore
≤: less than or equal to
≥: greater than or equal to
∞: infinity
LOGnX: logx to the base n
xn: the nth power of x
f(x): the function of x
dx: diffrencial of x
x+y: x plus y
(a+b): bracket a plus b bracket closed
a=b: a equals b
a≠b: a isn't equal to b
a>b : a is greater than b
a>>b: a is much greater than b
a≥b: a is greater than or equal to b
x→∞: approches infinity
x2: x square
x3: x cube
√ ̄x: the square root of x
3√ ̄x: the cube root of x
3‰: three peimill
n∑i=1xi: the summation of x where x goes from 1to n
n∏i=1xi: the product of x sub i where igoes from 1to n
∫ab: integral betweens a and b
数学符号(理科符号)——运算符号 :
1.基本符号:+ - × ÷(/)
2.分数号:/
3.正负号:±
4.相似全等:∽ ≌
5.因为所以:∵ ∴
6.判断类:= ≠ < ≮(不小于) > ≯(不大于)
7.集合类:∈(属于) ∪(并集) ∩(交集)
8.求和符号:∑
9.n次方符号:¹(一次方) ²(平方) ³(立方) ⁴(4次方) ⁿ(n次方)
10.下角标:₁ ₂ ₃ ₄
(如:A₁B₂C₃D₄ 效果如何?)
11.或与非的"非":¬
12.导数符号(备注符号):′ 〃
13.度:° ℃
14.任意:∀ ;“存在”:∃
15.推出号:⇒
16.等价号:⇔
17.包含被包含:⊆ ⊇ ⊂ ⊃
18.积分:∫ ∬
19.箭头类:↗ ↙ ↖ ↘ ↑ ↓ ↔ ↕ ↑ ↓ → ←
20.绝对值:|
21.弧:⌒
22.圆:⊙
点积(内积) 与 叉积(外积)
1. 向量的点积与叉积
1.1 向量的点积 (内积)
数量积又称标量积(Scalar product)、点积(Dot product),在欧几里得空间(Euclidean space)中称为内积(Inner product),对应元素相乘相加,结果是一个标量(即一个数),即是数量而不是向量。
定义:
两个向量 a与b的内积为 a·b = |a||b|cos∠(a, b),特别地,0·a =a·0 = 0;
若a,b是非零向量,则a与b****正交的充要条件是a·b = 0。
n维向量:两向量执行点乘操作(即对应位相乘后求和),如下:
几何意义
内积(点乘)的几何意义包括:
- 表征或计算两个向量之间的夹角
- b向量在a向量方向上的投影
有公式:
推导过程如下,首先看一下向量组成:
定义向量c:
根据三角形余弦定理(这里a、b、c均为向量,下同)有:
根据关系c=a-b有:
即:a∙b=|a||b|cos(θ)
向量a,b的长度都是可以计算的已知量,从而有a和b间的夹角θ:θ=arccos(a∙b|a||b|)
进而可以进一步判断两个向量是否同一方向或正交(即垂直)等方向关系,具体对应关系为:
a∙b>0→方向基本相同,夹角在0°到90°之间
a∙b=0→ 正交,相互垂直
a∙b<0→ 方向基本相反,夹角在90°到180°之间
numpy 中 使用
np.dot或numpy.inner()实现向量的点积例:
import numpy as np a = np.array([1,2,3]) b = np.array([4,5,6]) ## 数量积 使用np.dot或np.inner print(np.dot(a,b))
1.2 向量的叉积 (外积)
向量积又称矢量积(Vector product)、叉积(Cross product)、外积(Outer product),结果是一个向量。
其运算结果是一个向量而不是一个标量。
并且两个向量的外积与这两个向量组成的坐标平面垂直。
定义:向量a与b的外积a×b是一个向量,其长度等于|a×b| = |a||b|sin∠(a,b),其方向正交于a与b。并且,(a,b,a×b)构成右手系。
特别地,0×a = a×0 = 0.此外,对任意向量a,a×a=0。对于向量a和向量b:
a和b的外积公式为:
其中:
根据i、j、k间关系,有:
即
根据i、j、k间关系,有:
几何意义
在三维几何中,向量a和向量b的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,外积的概念非常有用,可以通过两个向量的外积,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
在二维空间中,外积还有另外一个几何意义就是:
|a×b|在数值上等于由向量a和向量b构成的平行四边形的面积。
numpy中 使用
np.cross实现向量的叉积例:
import numpy as np a = np.array([1,2,3]) b = np.array([4,5,6]) ## 叉积 使用np.cross print(np.cross(a,b))
点积与叉积小结:

注:数量、向量常用于数学;而标量、矢量常用于物理
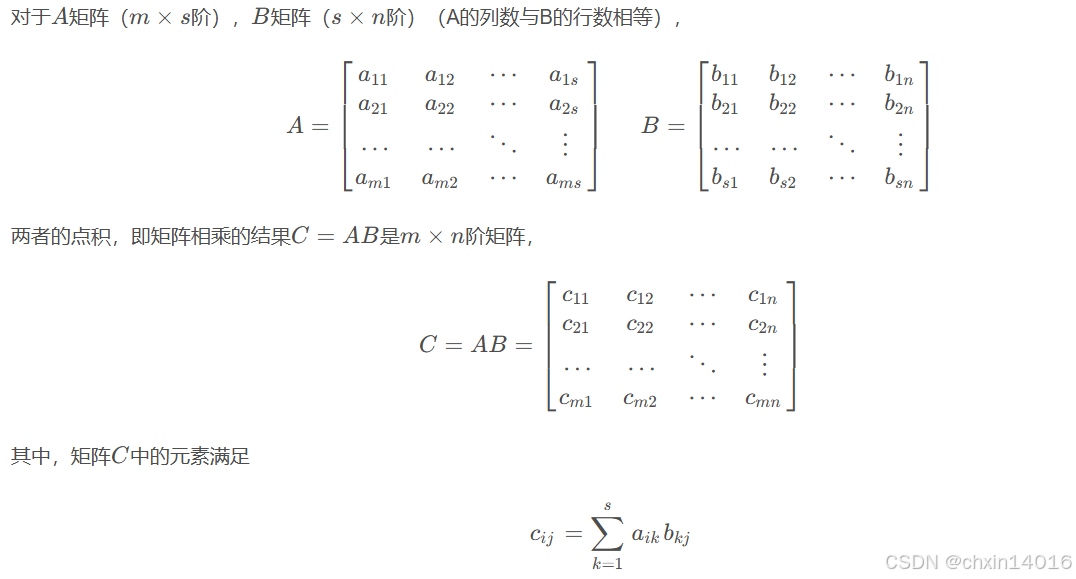
2 矩阵的点积与叉积
2.1 矩阵的点积 (内积)
【前找行,后找列,相乘相加】
例1:
numpy实现:
import numpy as np A1 = np.array([[1,2],[3,4]]) B2 = np.array([[5,6],[7,8]]) A2 = np.array([[1,2,3],[1,2,3]]) B2 = np.array([1,2,3]) ## 数量积 使用np.dot print(np.dot(A1,B1)) print(np.dot(A2,B2))此外,numpyt提供了
numpy.inner()函数,从字面意思理解是内积,其针对向量numpy.inner()与numpy.dot()输出一致,但针对矩阵有所不同。print(np.inner(A1,B1))输出为:
其中:
17 = 1×5+2×6, 23 = 1×7+2×8
39 = 3×5+4×6, 53 = 3×7+4×8
print(np.inner(A2,B2))输出为:[14 14]
例2:
X2 = np.array([[1,2,3],[1,2,3]])#2行3列 Y2 = np.array([1,2,3]) #3行1列 result = np.dot(X2,Y2) #数量积的结果为[14,14] result_array = np.array(result) result_array.shape #结果为两行一列
2.2 矩阵的叉积 (外积)
针对矩阵并不存在叉积的概念,numpy中针对矩阵的叉积运算是按照向量的叉积进行运算。
例:
numpy实现:
import numpy as np A1 = np.array([[1,2],[3,4]]) B1 = np.array([[5,6],[7,8]]) A2 = np.array([[1,2,3],[1,2,3]]) B2 = np.array([1,2,3]) ## 叉积 使用np.cross print(np.cross(A1,B1)) print(np.cross(A2,B2))
3. 元素积
元素积(element-wise product, point-wise product)又称哈达玛积(Hadamard product )、舒尔积、逐项积,对应元素相乘,结果还是向量/矩阵
numpy中 使用
np.multiply或*实现元素积例:
import numpy as np a = np.array([1,2,3]) b = np.array([4,5,6]) A1 = np.array([[1,2],[3,4]]) B1 = np.array([[5,6],[7,8]]) A2 = np.array([[1,2,3],[1,2,3]]) B2 = np.array([1,2,3]) ## 数量积 使用np.multiply或* print(np.multiply(a,b)) print(np.multiply(A1,B1)) print(np.multiply(A2,B2)) #阶数不一致的,numpy将进行广播确保一致
4. 克罗内克积
克罗内克积(Kronecker product)是两个任意大小的矩阵间的运算。
numpy中 使用
np.kron实现例:
import numpy as np A1 = np.array([1,2,3]) B1 = np.array([4,5,6]) A2 = np.array([[1,2],[3,4]]) B2 = np.array([[5,6],[7,8]]) A3 = np.array([[1,2,3],[1,2,3]]) B3 = np.array([1,2,3]) ## 克罗内克积 使用np.kron print(np.kron(A1,B1)) print(np.kron(A2,B2)) print(np.kron(A3,B3))
范数
微积分
微分和积分是微积分的两个分支,前者微分可应用于深度学习中的优化问题。
导数,偏导数,方向导数,梯度的理解---微积分数学基础
参考链接:导数,偏导数,方向导数,梯度的理解---微积分数学基础_u对法向量求偏导是什么-CSDN博客
导数:(对于一元函数)区域内的变化率,例如:速度。是仅含一个变量的函数的微分。
偏导数:(对于多元函数)垂直与各坐标轴的特殊切线的斜率(N元函数有N个偏导数)。
例如:(以二元函数为例),x轴/y轴方向上的导数即为偏导数。
方向导数:包括偏导数在内的,任意方向的带方向导数。
方向导数的最大值:方向导数方向与偏导向量同向时,取得最大值(梯度的模)。
反向时,取得负最大值。
(梯度方向为方向导数最大的方向,梯度的模为最大的方向导数)
某位置处,任意方向的方向导数为偏导数的线性组合,系数为该方向的单位向量。
当该方向与坐标轴正方向一致时,方向导数即偏导数。
换句话说,偏导数为坐标轴方向上的方向导数,其他方向的方向导数为偏导数的合成。
梯度:
几何意义:
- 梯度方向:当前位置的梯度方向,为函数在该位置处方向导数最大的方向,也是函数值上升最快的方向,反方向为下降最快的方向;
- 梯度长度(模):当前位置的梯度长度(模),为最大方向导数的值。
小结:
- 偏导数构成的向量为梯度;
- 方向导数为梯度在该方向上的合成,系数为该方向的单位向量;
- 梯度方向为方向导数最大的方向,梯度的模为最大的方向导数;
- 微分的结果为梯度与微分向量的内积
- 等高线全微分的结果为0,所以其梯度垂直于等高线,同时指向高度更高的等高线
- 隐函数的梯度为高维曲面(曲线)的法向量
导数和微分
-
导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率,也是瞬时变化区间
处函数图像下方的面积。

可微与可导的关系:可微是可导的充分条件
(可微更牛)
可微代表所有维度下导数存在,一元下两者等价。
一般情况下,
- 可微是可导的充分条件 [可微一定可导,可导不一定可微],
- 可导是连续的充分条件 [可导一定连续,连续不一定可导]。
一元函数下两者等价,可微必可导、可导必可微, 相对较简单,且可微和可导都可推出连续。
多元函数下可微就要求就相对比较高一些,可微必可偏导、可微必连续、可微必方向可导;但是反过来都不可以,即便连续+可偏导+方向可导三个一起都推不出可微。
即:
可微=》可导 =》连续 =》可偏导 =》方向可导;
但反过来时:一元则可逆,多元则不行。
求导公式
导数的等价符号 & 常见函数的求微分规则:
求微分的法则:
偏导数
导数:(对于一元函数)区域内的变化率,例如:速度。是仅含一个变量的函数的微分。
将微分的思想推广到多元函数(multivariate function)上,就是偏导数。
偏导数:(对于多元函数)垂直与各坐标轴的特殊切线的斜率(N元函数有N个偏导数)。
例如:(以二元函数为例),x轴/y轴方向上的导数即为偏导数。
-
梯度是一个向量,其分量是多变量函数相对于其所有变量的偏导数。
-
链式法则可以用来微分复合函数。
小结
微分和积分是微积分的两个分支,前者可以应用于深度学习中的优化问题。
导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率。
梯度是一个向量,其分量是多变量函数相对于其所有变量的偏导数。
链式法则可以用来微分复合函数。

























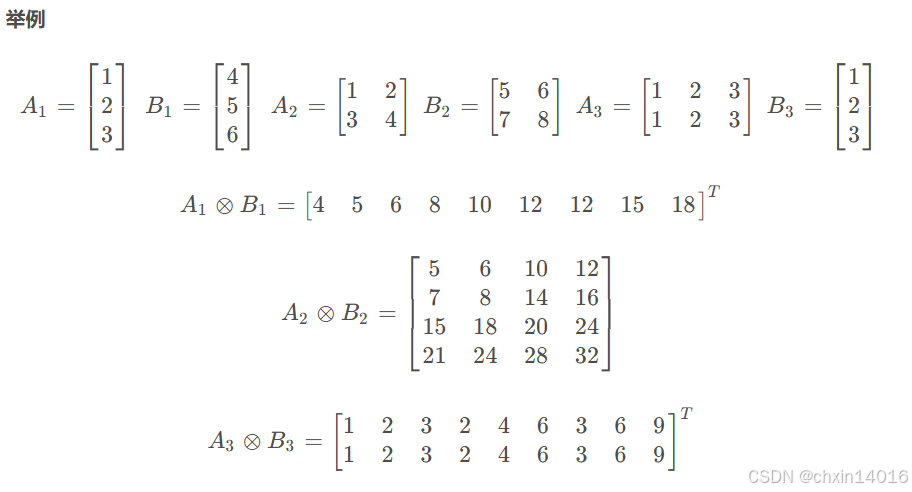






















 739
739

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








