关于此章重中之重并不是那些高深的定理、结论而是看似毫不起眼的“矩阵运算法则”,见前言。
目录
前言
矩阵运算与我们日常实数运算不同,故一些运算法则略有罗列,如下:
关于矩阵与常数运算:
、
、
、
;
关于矩阵之间的加法:
、
、
、
关于矩阵之间的乘法:
、
、
、
关于各类矩阵间的复合运算:
、
、
、
提示:以下是本篇文章正文内容,下面案例可供参考
一、关于高阶矩阵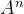
1.A为方阵且r(A)=1
则:;
2.找规律
(1):若,则
(2):若,则
、
3.分解(A=B+C)
(1):若,
则:【这里与高数中求高阶导数方法类似】
(2):再“(1)”的条件下,若,则
4.运用初等矩阵理解
若均为初等矩阵,m,n为正整数,则
表示对矩阵A作了与
相同的初等行变换,且重复m次;再对
作了与
相同的初等列变换,且重复n次。
5.运用相似理论求
(1):若则存在可逆矩阵
,使得
,
(2):若则存在可逆矩阵
,使得
,
二、关于伴随矩阵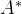
1.定义
原矩阵内所有元素都替换成对应的代数余子式,再转置即为“伴随矩阵”.
2.公式
(1):
(2):
(3):
(4):
、
(5):
(6):
(7):
(8):
(9):
(10):
3.关于伴随矩阵的秩【见下篇“矩阵的秩”】
三、关于逆矩阵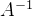
1.定义
对于方阵,若
,则
互为逆矩阵,且
【注:任何一个可逆矩阵必可由若干个初等矩阵乘积得来】
2.求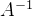
具体型: 、(初等行变换):
、(初等行变换):![[A|E]\rightarrow [E|A^{-1}]](https://latex.csdn.net/eq?%5BA%7CE%5D%5Crightarrow%20%5BE%7CA%5E%7B-1%7D%5D)
抽象型:
(1):创造,则
(2):创造若
均可逆,则
四、初等矩阵
1.定义
“初等变换”:(1):一个非零常数乘矩阵的某一行(列);
(2):互换矩阵中某两行(列)的位置;
(3):矩阵的某一行(列)的k倍加到另一行(列);
“初等矩阵”:由单位矩阵经过一次初等变换得到的矩阵成为初等矩阵。
2.左行右列定理
(1):矩阵左乘初等矩阵
,得
,相当于对
作了一次与
完全相同得初等行变换;
(2):矩阵右乘初等矩阵
,得
,相当于对
作了一次与
完全相同得初等列变换;
五、矩阵方程
1、定义
含有未知矩阵的方程成为矩阵方程;
2、化简
"消公因式":即若,且
可逆,则
;
"提取公因式":即;
"移项":即将已知表达式与位置表达式分别移至方程两边;
"利用公式".
3、求解
【注:理解此处需具备"方程组&向量组"相关知识】
(1):若或
,或
且
可逆,则分别可得解为 ·
(2):若不可逆,如
,则将
和
按列分块,得
,即
,求解上述线性方程组,得解
,从而得
(3)【待定系数法】:若无法化成上述几种形式,则应该设未知矩阵为,直接代入方程得到含未知量为
的线性方程组,求得矩阵X的元素
,从而求得未知矩阵。
总结
线代基础之三“矩阵方程”,呈上。






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








