本文详细探讨了多元函数极限的两种定义及其可能存在的问题，强调了定义方式选择对结果的影响。同时，列举了多元函数求极限的常见方法，如利用极限性质、有理化和整体替换。此外，还讨论了极坐标的运用以及何时可以将问题转化为一元函数处理。对于极限不存在的情况，指出必须通过不同路径来验证。最后，提到了如何利用多重积分定义求解极限。
一、多元函数极限的定义
存在的问题：有两种定义方式分别以 聚点/ 去心领域去定义重极限，不同的定义方式可能导致结果不同
用
定义证明的例题选解
二、多元函数求极限的方法
1、利用极限性质（四则运算法则、夹逼准则）
夹逼准则：多是夹为0。有界函数放缩为固定值/常用不等式？去分母？
2、消去分母中极限为 0 的因子 —— 有理化，等价无穷小代换
3、有界函数x无穷小量=0
4、直接代入：先代入看看是不是未定式！如果不是那就是答案
极坐标：
都可以考虑极坐标 ！
注意！x和y次数相同！
整体替换化为一元函数：可以分拆，可以整体代换的重极限可以尝试。当变成一元函数那方法就多了，如：等价，洛必达，泰勒......
注意：多元函数洛必达教材没有，不可用！
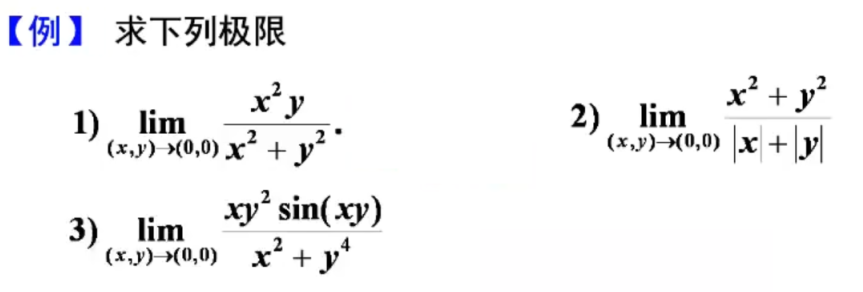
1）初步判断：三次比二次 —— 极限应为 0
利用
注：本题若用极坐标，只是恰巧和答案求得结果一样，过程是错误的！！！
因为当 ρ 趋向于 0时 ，θ 也在变，牵扯到了一致性的问题，超出了考研要求。
2）
3）
三、多元函数的极限不存在
注意：
只能最多说明极限不存在，不能说明极限存在！
强行找几条路径认为存在是逻辑错误，因为路径根本找不完。
—— 沿两种不同路径极限不同。
四、利用多重积分定义求极限
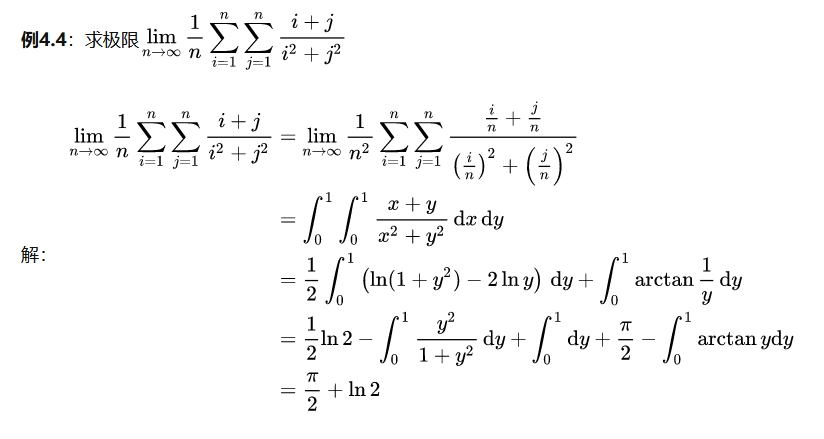
原文见
扫一扫
1796
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
