如何光明正大地“编数据“

最新推荐文章于 2025-04-28 23:03:26 发布
最新推荐文章于 2025-04-28 23:03:26 发布
阅读量939 收藏 22
点赞数 14
文章标签： 编程 生物 医药 excel
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_47195452/article/details/143281097
版权

写在前面

在R语言中，缺失值（NA，Not Available）是数据分析中常见的问题(尤其在处理大型数据集时)。在数据处理过程中，直接删除或认为填写缺失值都是错误的行为，我们需要利用R语言科学的"填写"缺失值处理。R提供了多种方法来检测、处理和替换缺失值，以确保分析结果的准确性和完整性。

1) 需要用到的包

VIM、mice missForest

2) 需要用到的数据集

VIM包中的哺乳动物sleep数据集。该数据集包含62种哺乳动物的睡眠类变量、生态学变量和体质类变量间的关系。睡眠类变量为因变量，另外两个为自变量。睡眠累变量包含做梦时长(Dream)、不做梦时长(NonD)和时长之和(Sleep);体质类变量包括体重(BodyWgt)、脑重(BrainWgt)、寿命(Span)、妊娠期(Gest);生态学变量包括物种被捕食的程度(Pred)、睡眠时的暴露程度(Exp)和面临的总危险度(Danger).

17.1 处理缺失值的步骤

1)识别缺失数据；

2)检查导致数据缺失的原因：缺失数据可以分为3类，完全随机缺失(MCAR),随机缺失(MAR)和非随机缺失(NMAR)。

3)删除包含缺失值的观测值或合理插补。

17.2 识别缺失值

R中使用NA代表缺失值；NaN代表不可能值；Inf和-Inf分别代表正无穷和负无穷值。

17.2.1 is.na()函数

可以识别NA和NaN，返回TRUE；若不是缺失值则返回FALSE。

17.2.2 complete.cases()函数

识别完整数据，返回TRUE；识别到NA和NaN，返回FALSE；

!complete.cases()函数是用于识别缺失值的，返回的结果与complete.cases()函数相反。

17.2.3 举例

y <- c(NA,NaN,Inf,-Inf,5)
is.na(y)
## [1]  TRUE  TRUE FALSE FALSE FALSE
complete.cases(y)
## [1] FALSE FALSE  TRUE  TRUE  TRUE
!complete.cases(y)
## [1]  TRUE  TRUE FALSE FALSE FALSE
library(VIM)
## Warning: 程辑包'VIM'是用R版本4.3.2 来建造的
## 载入需要的程辑包：colorspace
## VIM is ready to use.
## Suggestions and bug-reports can be submitted at: https://github.com/statistikat/VIM/issues
## 
## 载入程辑包：'VIM'
## The following objects are masked _by_ '.GlobalEnv':
## 
##     diabetes, testdata, wine
## The following object is masked from 'package:rattle':
## 
##     wine
## The following object is masked from 'package:datasets':
## 
##     sleep
data(sleep,package = "VIM")
is.na(sleep)
##       BodyWgt BrainWgt  NonD Dream Sleep  Span  Gest  Pred   Exp Danger
##  [1,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [2,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [3,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [4,]   FALSE    FALSE  TRUE  TRUE FALSE  TRUE FALSE FALSE FALSE  FALSE
##  [5,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [6,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [7,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [8,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
##  [9,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [10,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [11,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [12,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [13,]   FALSE    FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE  FALSE
## [14,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [15,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [16,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [17,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [18,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [19,]   FALSE    FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  FALSE
## [20,]   FALSE    FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  FALSE
## [21,]   FALSE    FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE  FALSE
## [22,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [23,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [24,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [25,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [26,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [27,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [28,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [29,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [30,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [31,]   FALSE    FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE  FALSE
## [32,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [33,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [34,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [35,]   FALSE    FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  FALSE
## [36,]   FALSE    FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  FALSE
## [37,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [38,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [39,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [40,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [41,]   FALSE    FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE  FALSE
## [42,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [43,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [44,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [45,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [46,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [47,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [48,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [49,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [50,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [51,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [52,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [53,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [54,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [55,]   FALSE    FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE  FALSE
## [56,]   FALSE    FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  FALSE
## [57,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [58,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [59,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [60,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [61,]   FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE
## [62,]   FALSE    FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE  FALSE
sleep[complete.cases(sleep),]#列出没有缺失值的行
##     BodyWgt BrainWgt NonD Dream Sleep  Span  Gest Pred Exp Danger
## 2     1.000     6.60  6.3   2.0   8.3   4.5  42.0    3   1      3
## 5  2547.000  4603.00  2.1   1.8   3.9  69.0 624.0    3   5      4
## 6    10.550   179.50  9.1   0.7   9.8  27.0 180.0    4   4      4
## 7     0.023     0.30 15.8   3.9  19.7  19.0  35.0    1   1      1
## 8   160.000   169.00  5.2   1.0   6.2  30.4 392.0    4   5      4
## 9     3.300    25.60 10.9   3.6  14.5  28.0  63.0    1   2      1
## 10   52.160   440.00  8.3   1.4   9.7  50.0 230.0    1   1      1
## 11    0.425     6.40 11.0   1.5  12.5   7.0 112.0    5   4      4
## 12  465.000   423.00  3.2   0.7   3.9  30.0 281.0    5   5      5
## 15    0.075     1.20  6.3   2.1   8.4   3.5  42.0    1   1      1
## 16    3.000    25.00  8.6   0.0   8.6  50.0  28.0    2   2      2
## 17    0.785     3.50  6.6   4.1  10.7   6.0  42.0    2   2      2
## 18    0.200     5.00  9.5   1.2  10.7  10.4 120.0    2   2      2
## 22   27.660   115.00  3.3   0.5   3.8  20.0 148.0    5   5      5
## 23    0.120     1.00 11.0   3.4  14.4   3.9  16.0    3   1      2
## 25   85.000   325.00  4.7   1.5   6.2  41.0 310.0    1   3      1
## 27    0.101     4.00 10.4   3.4  13.8   9.0  28.0    5   1      3
## 28    1.040     5.50  7.4   0.8   8.2   7.6  68.0    5   3      4
## 29  521.000   655.00  2.1   0.8   2.9  46.0 336.0    5   5      5
## 32    0.005     0.14  7.7   1.4   9.1   2.6  21.5    5   2      4
## 33    0.010     0.25 17.9   2.0  19.9  24.0  50.0    1   1      1
## 34   62.000  1320.00  6.1   1.9   8.0 100.0 267.0    1   1      1
## 37    0.023     0.40 11.9   1.3  13.2   3.2  19.0    4   1      3
## 38    0.048     0.33 10.8   2.0  12.8   2.0  30.0    4   1      3
## 39    1.700     6.30 13.8   5.6  19.4   5.0  12.0    2   1      1
## 40    3.500    10.80 14.3   3.1  17.4   6.5 120.0    2   1      1
## 42    0.480    15.50 15.2   1.8  17.0  12.0 140.0    2   2      2
## 43   10.000   115.00 10.0   0.9  10.9  20.2 170.0    4   4      4
## 44    1.620    11.40 11.9   1.8  13.7  13.0  17.0    2   1      2
## 45  192.000   180.00  6.5   1.9   8.4  27.0 115.0    4   4      4
## 46    2.500    12.10  7.5   0.9   8.4  18.0  31.0    5   5      5
## 48    0.280     1.90 10.6   2.6  13.2   4.7  21.0    3   1      3
## 49    4.235    50.40  7.4   2.4   9.8   9.8  52.0    1   1      1
## 50    6.800   179.00  8.4   1.2   9.6  29.0 164.0    2   3      2
## 51    0.750    12.30  5.7   0.9   6.6   7.0 225.0    2   2      2
## 52    3.600    21.00  4.9   0.5   5.4   6.0 225.0    3   2      3
## 54   55.500   175.00  3.2   0.6   3.8  20.0 151.0    5   5      5
## 57    0.900     2.60 11.0   2.3  13.3   4.5  60.0    2   1      2
## 58    2.000    12.30  4.9   0.5   5.4   7.5 200.0    3   1      3
## 59    0.104     2.50 13.2   2.6  15.8   2.3  46.0    3   2      2
## 60    4.190    58.00  9.7   0.6  10.3  24.0 210.0    4   3      4
## 61    3.500     3.90 12.8   6.6  19.4   3.0  14.0    2   1      1
sum(is.na(sleep$Dream))#计算Dream缺失值有几个
## [1] 12
mean(is.na(sleep$Dream))#计算 sleep$Dream 列中缺失值的比例
## [1] 0.1935484

注意：这里的mean()不是用来求均值，而是计算一个逻辑向量中 TRUE 的比例。

17.3 缺失值的可视化

17.3.1 mice包中的md.pattern()函数

该函数生成一个矩阵或数据框形式展示缺失值模式的表格，和用该表格绘制成的图形。

  • 17.3.1.1 语法
library(mice)
md.pattern(x,plot=,rotate.names=)

x：一个含有缺失值的数据框；

plot:默认为TRUE，作图；

rotate.names：变量名称在图中的排列方式，是水平放置还是垂直放置。默认值为 ‘rotate.names = FALSE’，即不旋转变量名称，水平放置。当为TRUE时，则为垂直放置。

  • 17.3.1.2 举例
library(mice)
## Warning: 程辑包'mice'是用R版本4.3.2 来建造的
## 
## 载入程辑包：'mice'
## The following objects are masked from 'package:flexclust':
## 
##     bwplot, densityplot
## The following object is masked from 'package:stats':
## 
##     filter
## The following objects are masked from 'package:base':
## 
##     cbind, rbind
data(sleep,package = "VIM")
md.pattern(sleep,plot=TRUE,rotate.names=TRUE)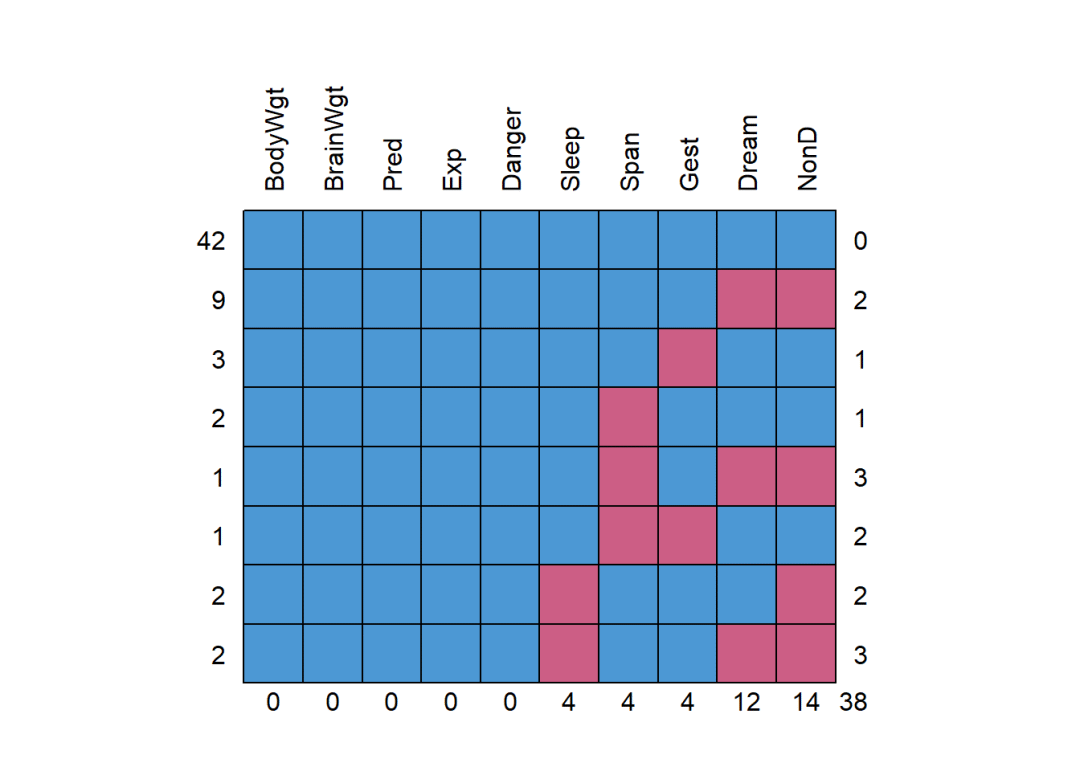

##    BodyWgt BrainWgt Pred Exp Danger Sleep Span Gest Dream NonD   
## 42       1        1    1   1      1     1    1    1     1    1  0
## 9        1        1    1   1      1     1    1    1     0    0  2
## 3        1        1    1   1      1     1    1    0     1    1  1
## 2        1        1    1   1      1     1    0    1     1    1  1
## 1        1        1    1   1      1     1    0    1     0    0  3
## 1        1        1    1   1      1     1    0    0     1    1  2
## 2        1        1    1   1      1     0    1    1     1    0  2
## 2        1        1    1   1      1     0    1    1     0    0  3
##          0        0    0   0      0     4    4    4    12   14 38

结果解释：

1.列表中的0表示有缺失值，1表示没有缺失值。第1列表示各缺失值的观测值个数，最后1列表示各模式中有缺失值的个数。从第一行可以看出共42个观测值没有缺失值。最后一行为每个变量中缺失值的数目。

2.格子图片中，蓝色的为非缺失值，红色的为缺失值。左侧数据相当于列表中的第一列，为观测值的数目；右侧相当于列表的最后一列，为缺失值的个数。下面为各变量中缺失值的总数。

17.3.2 VIM包中的aggr()函数

  • 17.3.2.1 语法
library(VIM)
aggr(x,prop=,numbers=)

x:数据框；

prop:一个逻辑值，指示是否使用缺失/插补值和组合的比例，而不是总数。prop=TRUE,返回的是指数形式，prop=FALSE时返回的是数字形式；

numbers：一个逻辑值，指示不同组合的比例或频率是否应该用数字表示。当=FALSE(默认)时，则删去数值型标签。

  • 17.3.2.2 举例
library(VIM)
aggr(sleep,prop=FALSE,numbers=TRUE)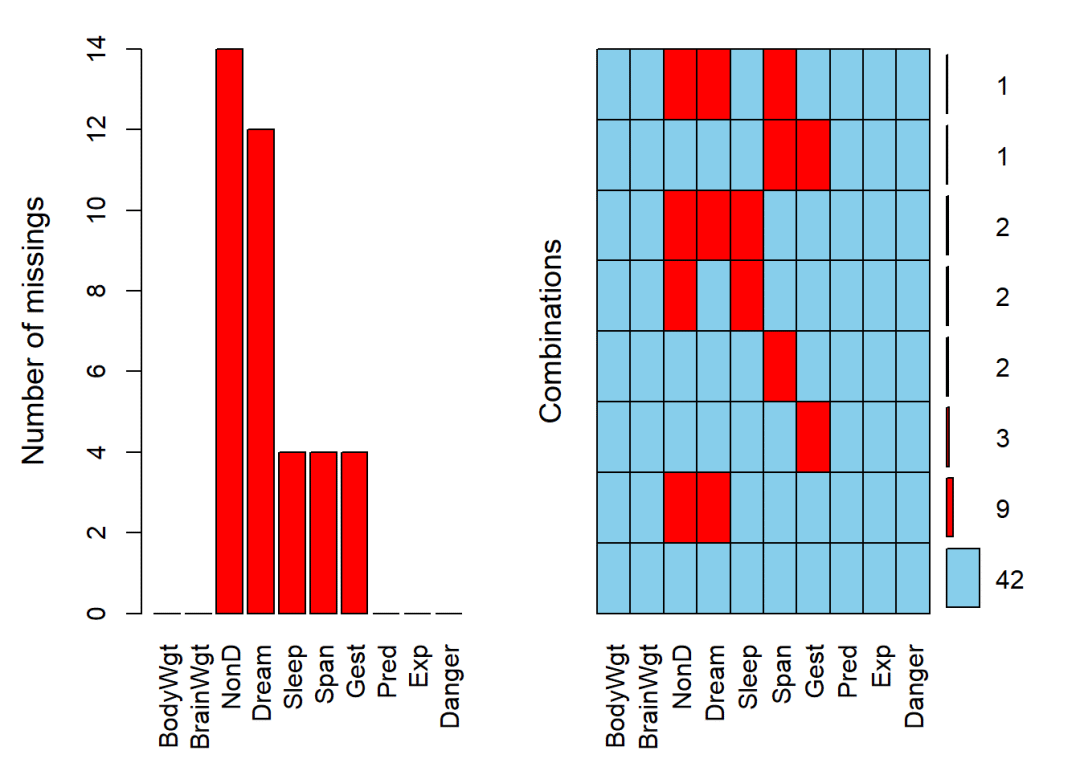

左图中红色柱为含缺失值的变量中缺失值的数目，右图中蓝色为非缺失值，红色为缺失值，右侧数字为有这些缺失值的观测值数量。

17.4 删除缺失值

主要包括行删除和成对删除，其中成对删除用的很少，且会导致数据的一些扭曲，故不推荐。

17.4.1 行删除(na.omit()函数)

newdata <- na.omit(sleep)
aggr(sleep)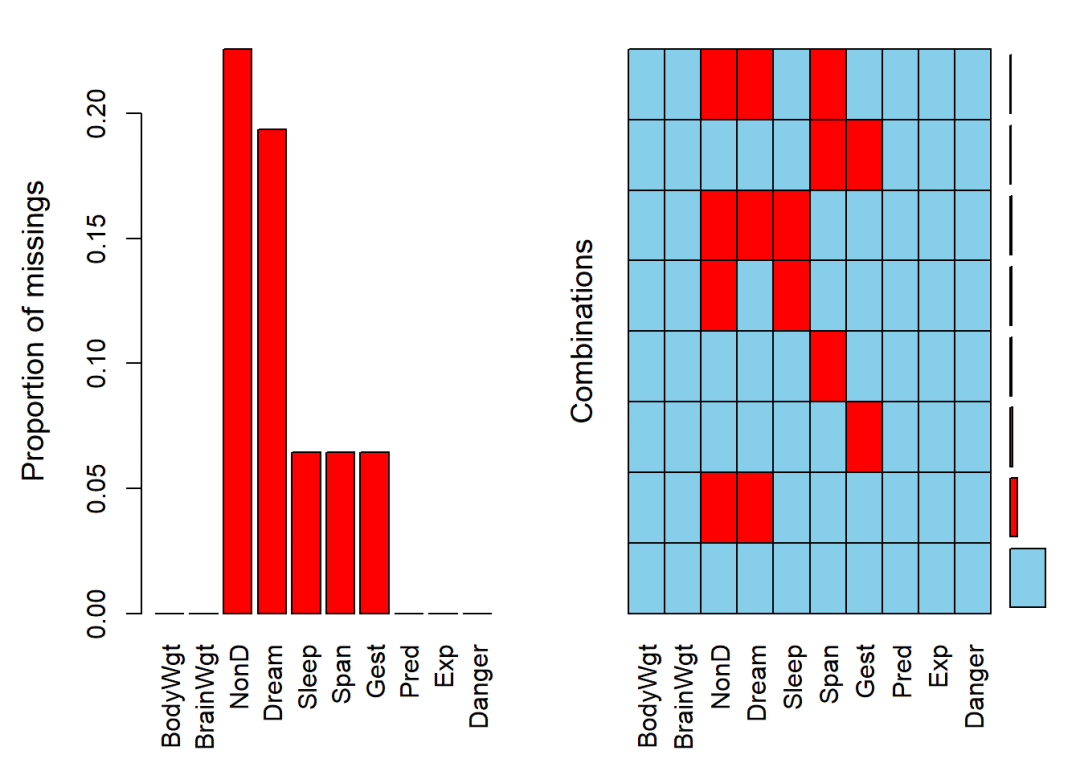

aggr(newdata)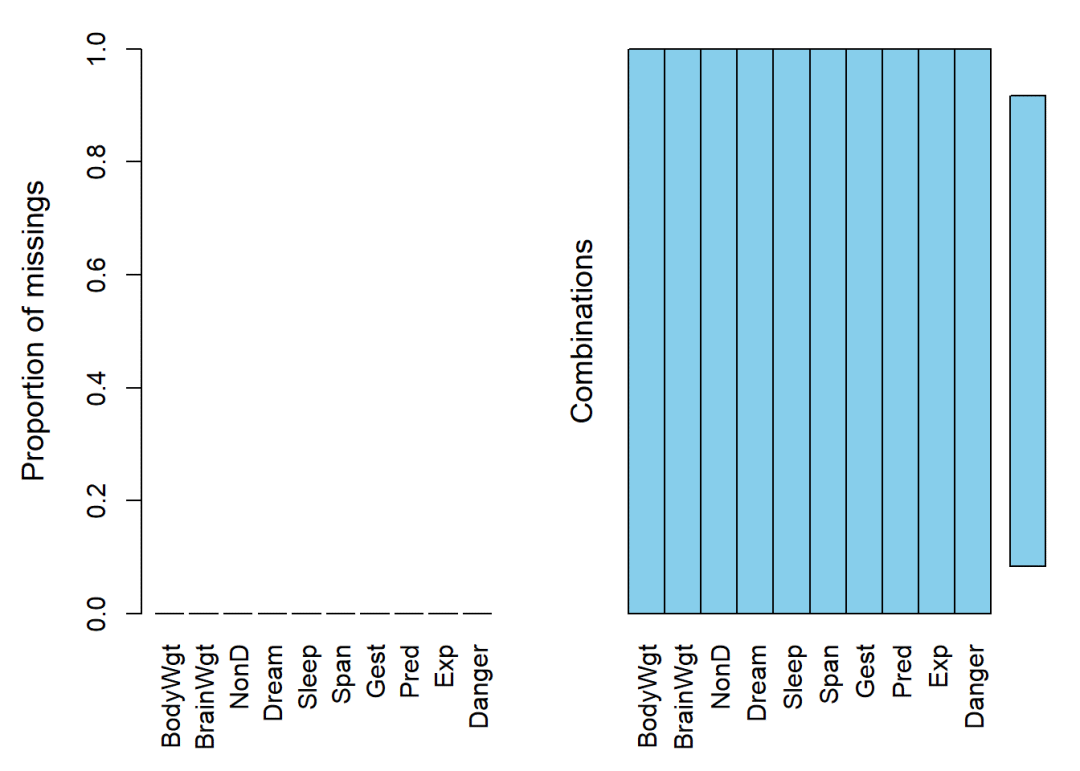

summary(sleep)
##     BodyWgt            BrainWgt            NonD            Dream      
##  Min.   :   0.005   Min.   :   0.14   Min.   : 2.100   Min.   :0.000  
##  1st Qu.:   0.600   1st Qu.:   4.25   1st Qu.: 6.250   1st Qu.:0.900  
##  Median :   3.342   Median :  17.25   Median : 8.350   Median :1.800  
##  Mean   : 198.790   Mean   : 283.13   Mean   : 8.673   Mean   :1.972  
##  3rd Qu.:  48.202   3rd Qu.: 166.00   3rd Qu.:11.000   3rd Qu.:2.550  
##  Max.   :6654.000   Max.   :5712.00   Max.   :17.900   Max.   :6.600  
##                                       NA's   :14       NA's   :12     
##      Sleep            Span              Gest             Pred      
##  Min.   : 2.60   Min.   :  2.000   Min.   : 12.00   Min.   :1.000  
##  1st Qu.: 8.05   1st Qu.:  6.625   1st Qu.: 35.75   1st Qu.:2.000  
##  Median :10.45   Median : 15.100   Median : 79.00   Median :3.000  
##  Mean   :10.53   Mean   : 19.878   Mean   :142.35   Mean   :2.871  
##  3rd Qu.:13.20   3rd Qu.: 27.750   3rd Qu.:207.50   3rd Qu.:4.000  
##  Max.   :19.90   Max.   :100.000   Max.   :645.00   Max.   :5.000  
##  NA's   :4       NA's   :4         NA's   :4                       
##       Exp            Danger     
##  Min.   :1.000   Min.   :1.000  
##  1st Qu.:1.000   1st Qu.:1.000  
##  Median :2.000   Median :2.000  
##  Mean   :2.419   Mean   :2.613  
##  3rd Qu.:4.000   3rd Qu.:4.000  
##  Max.   :5.000   Max.   :5.000  
##
summary(newdata)
##     BodyWgt             BrainWgt            NonD            Dream      
##  Min.   :   0.0050   Min.   :   0.14   Min.   : 2.100   Min.   :0.000  
##  1st Qu.:   0.3162   1st Qu.:   3.60   1st Qu.: 6.150   1st Qu.:0.900  
##  Median :   2.2500   Median :  12.20   Median : 8.500   Median :1.650  
##  Mean   : 100.8139   Mean   : 218.68   Mean   : 8.743   Mean   :1.900  
##  3rd Qu.:  10.4125   3rd Qu.: 155.50   3rd Qu.:11.000   3rd Qu.:2.375  
##  Max.   :2547.0000   Max.   :4603.00   Max.   :17.900   Max.   :6.600  
##      Sleep            Span             Gest            Pred      
##  Min.   : 2.90   Min.   :  2.00   Min.   : 12.0   Min.   :1.000  
##  1st Qu.: 8.05   1st Qu.:  5.25   1st Qu.: 32.0   1st Qu.:2.000  
##  Median : 9.80   Median : 11.20   Median : 90.0   Median :3.000  
##  Mean   :10.64   Mean   : 19.37   Mean   :129.9   Mean   :2.952  
##  3rd Qu.:13.60   3rd Qu.: 27.00   3rd Qu.:195.0   3rd Qu.:4.000  
##  Max.   :19.90   Max.   :100.00   Max.   :624.0   Max.   :5.000  
##       Exp            Danger    
##  Min.   :1.000   Min.   :1.00  
##  1st Qu.:1.000   1st Qu.:1.25  
##  Median :2.000   Median :2.50  
##  Mean   :2.357   Mean   :2.69  
##  3rd Qu.:3.750   3rd Qu.:4.00  
##  Max.   :5.000   Max.   :5.00

aggr和summary的结果均显示，sleep中存在NA，而newdata中不存在NA。

我们再看一下共删除了多少行观测值：

nrow(newdata)
## [1] 42
nrow(sleep)
## [1] 62

这里看到，行删除后只剩42行，而原来有62行，共删除了20行观测值。有些缺失值遍布到观测值的数目较多，使用这一方法可能会导致删除的观测值过多而对结果产生一定误差。那么也可以使用插补的方法来对数据缺失值进行预处理。

17.5 单一插补

17.5.1 简单插补(simple imputation)

即用某个值(均值、中位数或众数)来替换变量中的缺失值。针对连续型变量，比较推荐使用中位数；针对分类型变量一般用众数进行简单插补。

  • 17.5.1.1 语法

zoo包中的na.aggregate()函数

library(zoo)
na.aggregate(object, by = 1, ..., FUN = mean,
             na.rm = FALSE, maxgap = Inf)

object:进行插补的对象，一般是某数据集中的某一变量，例如sleep$NonD

FUN:mean,均值插补；median，中位数插补；mode，众数插补

na.rm：逻辑值。是否应该删除剩余的缺失值？，默认为FALSE

  • 17.5.1.2 举例
library(zoo)
summary(sleep$NonD)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##   2.100   6.250   8.350   8.673  11.000  17.900      14
sleep$NonD <- na.aggregate(sleep$NonD, by = 1, FUN = median,
             na.rm = FALSE, maxgap = Inf)
summary(sleep$NonD)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    2.10    6.80    8.35    8.60   10.55   17.90

可以看到，按中位数插补后，中位数和最小值和最大值都没有变化，均值稍微变了一点但变化不大。

17.5.2 k邻近插补

对于具有一个或多个缺失值的观测值，找到与其最相似但具有值(数值完整)的观测值，然后利用这些观测值进行插补。

该方法适用于观测值小于1000的小-中型数据集，针对更大的数据集可以使用missForest插补。

  • 17.5.2.1 语法

使用VIM包中的kNN()函数,详细用法见VIM::kNN；在k邻近插补中，连续缺失值的汇总值时k个(一般是5个)最邻近值的中位数，类别型缺失值则使用众数。

library(VIM)
kNN(data)
  • 17.5.2.2 举例
library(VIM)
head(sleep)
##    BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
## 1 6654.000   5712.0 8.35    NA   3.3 38.6  645    3   5      3
## 2    1.000      6.6 6.30   2.0   8.3  4.5   42    3   1      3
## 3    3.385     44.5 8.35    NA  12.5 14.0   60    1   1      1
## 4    0.920      5.7 8.35    NA  16.5   NA   25    5   2      3
## 5 2547.000   4603.0 2.10   1.8   3.9 69.0  624    3   5      4
## 6   10.550    179.5 9.10   0.7   9.8 27.0  180    4   4      4
sleep_imp <- kNN(sleep)
head(sleep_imp)
##    BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger BodyWgt_imp
## 1 6654.000   5712.0 8.35   0.8   3.3 38.6  645    3   5      3       FALSE
## 2    1.000      6.6 6.30   2.0   8.3  4.5   42    3   1      3       FALSE
## 3    3.385     44.5 8.35   2.3  12.5 14.0   60    1   1      1       FALSE
## 4    0.920      5.7 8.35   2.4  16.5  3.2   25    5   2      3       FALSE
## 5 2547.000   4603.0 2.10   1.8   3.9 69.0  624    3   5      4       FALSE
## 6   10.550    179.5 9.10   0.7   9.8 27.0  180    4   4      4       FALSE
##   BrainWgt_imp NonD_imp Dream_imp Sleep_imp Span_imp Gest_imp Pred_imp Exp_imp
## 1        FALSE    FALSE      TRUE     FALSE    FALSE    FALSE    FALSE   FALSE
## 2        FALSE    FALSE     FALSE     FALSE    FALSE    FALSE    FALSE   FALSE
## 3        FALSE    FALSE      TRUE     FALSE    FALSE    FALSE    FALSE   FALSE
## 4        FALSE    FALSE      TRUE     FALSE     TRUE    FALSE    FALSE   FALSE
## 5        FALSE    FALSE     FALSE     FALSE    FALSE    FALSE    FALSE   FALSE
## 6        FALSE    FALSE     FALSE     FALSE    FALSE    FALSE    FALSE   FALSE
##   Danger_imp
## 1      FALSE
## 2      FALSE
## 3      FALSE
## 4      FALSE
## 5      FALSE
## 6      FALSE

结果显示，sleep_imp数据框中新添加了10个变量，即原变量_imp，这是kNN()函数默认添加的，可以使用imp_var=FALSE来阻止这10个变量的添加。

library(VIM)
sleep_imp1 <- kNN(sleep,imp_var = FALSE)
head(sleep_imp1)
##    BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
## 1 6654.000   5712.0 8.35   0.8   3.3 38.6  645    3   5      3
## 2    1.000      6.6 6.30   2.0   8.3  4.5   42    3   1      3
## 3    3.385     44.5 8.35   2.3  12.5 14.0   60    1   1      1
## 4    0.920      5.7 8.35   2.4  16.5  3.2   25    5   2      3
## 5 2547.000   4603.0 2.10   1.8   3.9 69.0  624    3   5      4
## 6   10.550    179.5 9.10   0.7   9.8 27.0  180    4   4      4

17.5.3 missForest 插补

主要针对大型数据集(观测值大于500-1000)，使用随机森林法来插补缺失值。

  • 17.5.3.1 语法

missForest包中的missForest()函数,详细用法见missForest::missForest

library(missForest)
set.seed()
missForest(xmis)$ximp

xmis:一个包含缺失值的数据矩阵。列对应于变量，行对应于观测值。

这里使用set.seed()函数是为了使结果具有重复性。

  • 17.5.3.2 举例
library(missForest)
## Warning: 程辑包'missForest'是用R版本4.3.2 来建造的
## 
## 载入程辑包：'missForest'
## The following object is masked from 'package:VIM':
## 
##     nrmse
set.seed(1234)
sleep_missForest <- missForest(sleep)$ximp
head(sleep)
##    BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
## 1 6654.000   5712.0 8.35    NA   3.3 38.6  645    3   5      3
## 2    1.000      6.6 6.30   2.0   8.3  4.5   42    3   1      3
## 3    3.385     44.5 8.35    NA  12.5 14.0   60    1   1      1
## 4    0.920      5.7 8.35    NA  16.5   NA   25    5   2      3
## 5 2547.000   4603.0 2.10   1.8   3.9 69.0  624    3   5      4
## 6   10.550    179.5 9.10   0.7   9.8 27.0  180    4   4      4
head(sleep_missForest)
##    BodyWgt BrainWgt NonD Dream Sleep   Span Gest Pred Exp Danger
## 1 6654.000   5712.0 8.35 1.350   3.3 38.600  645    3   5      3
## 2    1.000      6.6 6.30 2.000   8.3  4.500   42    3   1      3
## 3    3.385     44.5 8.35 2.333  12.5 14.000   60    1   1      1
## 4    0.920      5.7 8.35 2.524  16.5  6.934   25    5   2      3
## 5 2547.000   4603.0 2.10 1.800   3.9 69.000  624    3   5      4
## 6   10.550    179.5 9.10 0.700   9.8 27.000  180    4   4      4

$ximp 是从插补结果中提取出填补后的数据矩阵。

17.6 多重插补(multiple imputation, MI)

是一种基于重复模拟的处理缺失值的方法。当面对复杂的缺失值问题时，MI最常用。MI是从一个包含缺失值的数据集中生成一组(3-10个)对应的完整的数据集，这些数据集为模拟数据集，缺失数据将用蒙特卡罗法填充。R中可以使用mice、Amelia和mi包执行，这里介绍mice包的用法。

17.6.1 语法

1.插补

library(mice)
imp <- mice(data,m)
fit <- with(imp,analysis)
pooled <- pool(fit)
summary(pooled)

data:一个包含缺失值的矩阵或数据库；

imp：一个包含m个插补数据集(模拟数据集)的列表和对象，同时含有完整插补过程的信息。默认m=5，也可以设置为其他值，m为模拟数据集的数目；

analysis：一个表达式对象，用来设定应用于m个插补数据集的统计分析方法，包括线性回归模型的lm()函数，广义线性模型的glm()函数、广义可加模型的gam()；

fit：一个包含m个单独统计分析结果的列表对象；

pooled：一个包含m个统计分析平均结果的列表对象。

注意：如果仅用lm()函数无法在多重插补的基础上建立回归模型，所以需要借助with和pool函数。

2.查看

插补的结果保存在imp$imp中，可以查看其中任一变量的插补结果；也可以查看完整的插补数据集：

Hide

imp$imp$变量
complete(imp,action = n)

1.通过提取imp对象的子成分，可以观测到实际的插补值；

2.complete()函数用来查看m个插补数据集(模拟数据集)中的任意一个，其中n为1时则查看第一个插补数据集，n为5时则查看第5个插补数据集。n不会大于m。

17.6.2 举例

library(mice)
imp <- mice(sleep,method="rf",seed=1234,m=5)
## 
##  iter imp variable
##   1   1  Dream  Sleep  Span  Gest
##   1   2  Dream  Sleep  Span  Gest
##   1   3  Dream  Sleep  Span  Gest
##   1   4  Dream  Sleep  Span  Gest
##   1   5  Dream  Sleep  Span  Gest
##   2   1  Dream  Sleep  Span  Gest
##   2   2  Dream  Sleep  Span  Gest
##   2   3  Dream  Sleep  Span  Gest
##   2   4  Dream  Sleep  Span  Gest
##   2   5  Dream  Sleep  Span  Gest
##   3   1  Dream  Sleep  Span  Gest
##   3   2  Dream  Sleep  Span  Gest
##   3   3  Dream  Sleep  Span  Gest
##   3   4  Dream  Sleep  Span  Gest
##   3   5  Dream  Sleep  Span  Gest
##   4   1  Dream  Sleep  Span  Gest
##   4   2  Dream  Sleep  Span  Gest
##   4   3  Dream  Sleep  Span  Gest
##   4   4  Dream  Sleep  Span  Gest
##   4   5  Dream  Sleep  Span  Gest
##   5   1  Dream  Sleep  Span  Gest
##   5   2  Dream  Sleep  Span  Gest
##   5   3  Dream  Sleep  Span  Gest
##   5   4  Dream  Sleep  Span  Gest
##   5   5  Dream  Sleep  Span  Gest
fit <- with(imp,lm(Dream~Span+Gest))
pooled <- pool(fit)
summary(pooled)
##          term     estimate   std.error  statistic       df      p.value
## 1 (Intercept)  2.486829211 0.260066801  9.5622709 42.70262 3.541325e-12
## 2        Span -0.006983738 0.011828155 -0.5904335 54.65253 5.573338e-01
## 3        Gest -0.003299397 0.001527141 -2.1605066 40.91960 3.664093e-02
imp$imp$Dream
##      1   2   3   4   5
## 1  1.0 1.8 0.6 0.7 1.8
## 3  1.8 2.3 2.0 1.8 2.4
## 4  3.4 3.4 2.6 1.4 1.4
## 14 0.6 0.7 0.8 0.5 0.9
## 24 0.8 1.3 1.2 1.2 1.2
## 26 3.4 4.1 2.4 3.6 1.4
## 30 3.4 3.9 1.4 1.9 1.2
## 31 1.2 0.9 1.4 1.2 0.6
## 47 1.9 2.4 2.4 0.9 2.0
## 53 0.0 0.6 0.6 0.5 0.5
## 55 1.8 0.9 0.8 0.9 1.2
## 62 2.0 0.5 3.1 1.2 0.0
complete(imp,action = 2)
##     BodyWgt BrainWgt  NonD Dream Sleep  Span  Gest Pred Exp Danger
## 1  6654.000  5712.00  8.35   1.8   3.3  38.6 645.0    3   5      3
## 2     1.000     6.60  6.30   2.0   8.3   4.5  42.0    3   1      3
## 3     3.385    44.50  8.35   2.3  12.5  14.0  60.0    1   1      1
## 4     0.920     5.70  8.35   3.4  16.5   9.0  25.0    5   2      3
## 5  2547.000  4603.00  2.10   1.8   3.9  69.0 624.0    3   5      4
## 6    10.550   179.50  9.10   0.7   9.8  27.0 180.0    4   4      4
## 7     0.023     0.30 15.80   3.9  19.7  19.0  35.0    1   1      1
## 8   160.000   169.00  5.20   1.0   6.2  30.4 392.0    4   5      4
## 9     3.300    25.60 10.90   3.6  14.5  28.0  63.0    1   2      1
## 10   52.160   440.00  8.30   1.4   9.7  50.0 230.0    1   1      1
## 11    0.425     6.40 11.00   1.5  12.5   7.0 112.0    5   4      4
## 12  465.000   423.00  3.20   0.7   3.9  30.0 281.0    5   5      5
## 13    0.550     2.40  7.60   2.7  10.3   4.7  28.0    2   1      2
## 14  187.100   419.00  8.35   0.7   3.1  40.0 365.0    5   5      5
## 15    0.075     1.20  6.30   2.1   8.4   3.5  42.0    1   1      1
## 16    3.000    25.00  8.60   0.0   8.6  50.0  28.0    2   2      2
## 17    0.785     3.50  6.60   4.1  10.7   6.0  42.0    2   2      2
## 18    0.200     5.00  9.50   1.2  10.7  10.4 120.0    2   2      2
## 19    1.410    17.50  4.80   1.3   6.1  34.0 310.0    1   2      1
## 20   60.000    81.00 12.00   6.1  18.1   7.0 164.0    1   1      1
## 21  529.000   680.00  8.35   0.3   3.9  28.0 400.0    5   5      5
## 22   27.660   115.00  3.30   0.5   3.8  20.0 148.0    5   5      5
## 23    0.120     1.00 11.00   3.4  14.4   3.9  16.0    3   1      2
## 24  207.000   406.00  8.35   1.3  12.0  39.3 252.0    1   4      1
## 25   85.000   325.00  4.70   1.5   6.2  41.0 310.0    1   3      1
## 26   36.330   119.50  8.35   4.1  13.0  16.2  63.0    1   1      1
## 27    0.101     4.00 10.40   3.4  13.8   9.0  28.0    5   1      3
## 28    1.040     5.50  7.40   0.8   8.2   7.6  68.0    5   3      4
## 29  521.000   655.00  2.10   0.8   2.9  46.0 336.0    5   5      5
## 30  100.000   157.00  8.35   3.9  10.8  22.4 100.0    1   1      1
## 31   35.000    56.00  8.35   0.9   3.8  16.3  33.0    3   5      4
## 32    0.005     0.14  7.70   1.4   9.1   2.6  21.5    5   2      4
## 33    0.010     0.25 17.90   2.0  19.9  24.0  50.0    1   1      1
## 34   62.000  1320.00  6.10   1.9   8.0 100.0 267.0    1   1      1
## 35    0.122     3.00  8.20   2.4  10.6   3.9  30.0    2   1      1
## 36    1.350     8.10  8.40   2.8  11.2   4.7  45.0    3   1      3
## 37    0.023     0.40 11.90   1.3  13.2   3.2  19.0    4   1      3
## 38    0.048     0.33 10.80   2.0  12.8   2.0  30.0    4   1      3
## 39    1.700     6.30 13.80   5.6  19.4   5.0  12.0    2   1      1
## 40    3.500    10.80 14.30   3.1  17.4   6.5 120.0    2   1      1
## 41  250.000   490.00  8.35   1.0  10.9  23.6 440.0    5   5      5
## 42    0.480    15.50 15.20   1.8  17.0  12.0 140.0    2   2      2
## 43   10.000   115.00 10.00   0.9  10.9  20.2 170.0    4   4      4
## 44    1.620    11.40 11.90   1.8  13.7  13.0  17.0    2   1      2
## 45  192.000   180.00  6.50   1.9   8.4  27.0 115.0    4   4      4
## 46    2.500    12.10  7.50   0.9   8.4  18.0  31.0    5   5      5
## 47    4.288    39.20  8.35   2.4  12.5  13.7  63.0    2   2      2
## 48    0.280     1.90 10.60   2.6  13.2   4.7  21.0    3   1      3
## 49    4.235    50.40  7.40   2.4   9.8   9.8  52.0    1   1      1
## 50    6.800   179.00  8.40   1.2   9.6  29.0 164.0    2   3      2
## 51    0.750    12.30  5.70   0.9   6.6   7.0 225.0    2   2      2
## 52    3.600    21.00  4.90   0.5   5.4   6.0 225.0    3   2      3
## 53   14.830    98.20  8.35   0.6   2.6  17.0 150.0    5   5      5
## 54   55.500   175.00  3.20   0.6   3.8  20.0 151.0    5   5      5
## 55    1.400    12.50  8.35   0.9  11.0  12.7  90.0    2   2      2
## 56    0.060     1.00  8.10   2.2  10.3   3.5  30.0    3   1      2
## 57    0.900     2.60 11.00   2.3  13.3   4.5  60.0    2   1      2
## 58    2.000    12.30  4.90   0.5   5.4   7.5 200.0    3   1      3
## 59    0.104     2.50 13.20   2.6  15.8   2.3  46.0    3   2      2
## 60    4.190    58.00  9.70   0.6  10.3  24.0 210.0    4   3      4
## 61    3.500     3.90 12.80   6.6  19.4   3.0  14.0    2   1      1
## 62    4.050    17.00  8.35   0.5   5.4  13.0  38.0    3   1      1
aggr(complete(imp,action = 2))

第一个命令返回表展示了针对Dream变量的5次插补，第二个命令返回表展示了第2个完整的插补数据集。

1. 主要分析VIM包自带的数据集sleep中的缺失数据处理问题。
Mrrunsen的博客
01-20 802
【代码】1. 主要分析VIM包自带的数据集sleep中的缺失数据处理问题。
数据结构（四） -- C语言版 -- 线性表的链式存储 - 循环链表
青椒*^_^*凤爪爪的博客
03-13 9796
本文中没有涉及到很多的相关理论知识，也没有做深入的了解，所以，您如果是想要系统的学习、想要多学习关于理论的知识等，那么本文可能并不合适您。 本文中所有设计的代码均通过测试，并且在功能性方面均实现应有的功能。 设计的代码并非全部公开，部分无关紧要代码并没有贴出来。 如果你也对此感兴趣、也想测试源码的话，可以私聊我，非常欢迎一起探讨学习。 由于时间、水平、精力有限，文中难免会出现不准确、甚至错误的地方，也很欢迎大佬看见的话批评指正。 嘻嘻。。。。 。。。。。。。。收！
读书笔记_第十八章
阿拉丁
02-02 689
#处理缺失数据的高级方法 #解决缺失数据的两种方法： #1：删除含有缺失数据的实例 #2：用合理的替代之替换缺失值 #不管是哪种方法，最后的结果都是没有缺失值的数据集 #缺失数据的分类： #1 完全随机缺失 MCAR #若某变量的缺失数据与其他任何观测或未观测变量都不相关 #2 随机缺失 MAR #若某变量上的缺失数据与其他观测变量相关，而与自己的未观测值不相关 #3 非随机缺失 NMAR #...
R语言实战-第十八章 R处理缺失数据的高级方法
weixin_46964110的博客
01-17 2342
处理缺失数据的高级方法
如何光明正大地学习KISS？当然是用这个DL接吻检测器了
机器学习算法与Python学习
05-20 606
（给机器学习算法与Python学习加星标，提升AI技能）选自arXiv作者：Amir Ziai本文转自“机器之心”（almosthuman2014）不要误会。作为一个严肃的公众号，我...
python只保留数据的某几列_python获取索引 Python中怎么获取二维数组中指定列的数据。...
weixin_39582708的博客
11-25 848
如何在python列表中查找某个元素的索引方法二：利用enumerate函数。信任不是指没有误会而是总会给对方把误会解释清楚的机会python中索引取值可以从后往前取吗如果是取列表或者字符串的话，用切片应该是最简单的 例如：a = [1,2,3,4,5]print(a[-2:]) #结果是[4,5]小编总是勇敢的离开一个人却不懂如何巧妙的靠近一个人。b['state'].index("ohio")...
个人cf刷题 题目类型+一句话题意 记录
Accepted__的博客
09-21 832
个人cf刷题记录，包含题目类型及一句话题意
指针详解（一）
2301_80176226的博客
12-07 157
对指针的详解(一)
做运维&&数据中心停电了的那点事
灯塔微光
12-21 2266
摘要： 数据中心停电了，小编负责保障全校的网络及数据中心。很多专家就有疑惑了， 停电了，为何还要保障啥网络，出去Happy吧！**后附数据中心机房的标准规范 从专业角度来讲，我们应该考虑校内业务与校外业务，前端与后端。 一、停电后哪些业务可以中断？ 校内业务：前端可以中断，但后端数据存储依然仍需在线或手动关停。 校外业务：前后端都需在线。
2022 RoboCom CAIP(本科组)省赛个人题解
m0_72507689的博客
07-06 1326
2022 RoboCom CAIP(本科组)省赛个人题解
大数据时代之痛，你“裸奔”了吗？如何防止信息泄露
科多大数据的博客
11-02 3492
本文转载自科多大数据 作为一个热爱大数据的从业人员，我很不愿意去讨论这个话题（数据窃取、信息泄密），并且也不感兴趣。但现实生活中，很多公司就打着“大数据”的口号，做一些毫无技术含量的事，也就是随意窃取用户的隐私数据，再整合数据去暴力营销，或者对外提供数据服务（收费）。更有直接的就是“贩卖数据”，内外勾结去谋取私利，从而导致公民个人隐私信息像“冤魂”一样，漂泊流浪。 他们绞尽脑汁想去做的事，并不...
操作系统饥饿现象_操作系统原理之选择题
weixin_35904873的博客
01-13 1770
1. 下列选项中,操作系统提供给应用程序的接口是___A__。A.系统调用 B.中断 C.库函数 D.原语系统调用是操作系统提供给编程人员的唯一接口。--《计算机操作系统教程》2. 下列选项中,导致创建新进程的操作是___C___。I 用户登录成功 II 设备分配 III 启动程序执行A.仅 I 和 II B.仅 II 和 III C.仅 I 和 III D.I 、 II 和 III用户登录成功后...
面试官：这波HTTP究极combo，你顶得住吗？
chuhe1989的博客
10-09 852
基本概念 问题：HTTP 是什么？描述一下： HTTP 是超文本传输协议，也就是HyperText Transfer Protocol。 问题：能否详细解释「超文本传输协议」？ HTTP的名字「超文本协议传输」，它可以拆成三个部分： 协议 针对 HTTP 协议，我们可以这么理解。 HTTP 是文个⽤在计算机世界⾥的协议。它使⽤计算机能够理解的语⾔确⽴了⼀种计算机之间交流通信 的规范（两个以上的参与者），以及相关的各种控制和错误处理方式式（为约定和规范）。 传输 针对传输，我们可以进⼀步理解了 HT.
Python 操作 Excel 插入图表：解锁数据可视化的高效密码
weixin_44313745的博客
04-27 829
在数据分析与展示的领域中，Python 凭借其强大的库支持，成为众多开发者与数据工作者的得力助手。今天，就带大家深入探索如何利用 Python 在 Excel 中插入图表，实现数据可视化的进阶操作。掌握 Python 在 Excel 中插入图表的技能，能够为数据分析报告的制作、业务数据的可视化展示等工作带来极大的便利和效率提升，助力大家在数据处理与展示领域更加游刃有余。：专注于操作 Excel 2010 及以上版本的.xlsx 文件，支持在 Excel 工作表中添加、修改和读取数据，以及插入图表等操作。
使用多线程快速向Excel中快速插入一万条数据案例
weixin_38359768的博客
04-28 488
当出现问题时，调试和定位问题会变得非常困难，因为错误可能是由于线程之间的竞争条件、死锁等原因引起的，这些问题很难通过简单的日志和调试工具来排查。例如，多个线程同时访问磁盘、内存等资源，可能会导致资源瓶颈，反而降低了系统的性能。此外，线程的创建、销毁和切换都需要消耗一定的系统资源，过多的线程会增加系统的负担，导致性能下降。当一个线程在进行 I/O 操作（如将数据写入 Excel 文件）时，CPU 可能处于空闲状态，此时其他线程可以继续执行数据处理任务，避免了资源的闲置浪费，提高了系统的整体性能。
使用Python在excel里创建柱状图
最新发布
xll_007的博客
04-28 139
通过使用Python的openpyxl库，在excel里创建柱状图。openpyxl库提供了创建Excel图表的功能，包括柱状图(Bar Chart)。
Pandas 数据导出：如何将 DataFrame 追加到 Excel 的不同工作表
蜗牛沐雨
04-25 971
本文介绍了如何使用 Pandas 将 DataFrame 追加到 Excel 文件的不同工作表中，并在追加数据后自动调整列宽、处理零值、设置格式和添加背景色。通过类，我们可以灵活地控制数据的写入位置、工作表名称等。此外，我们还学习了如何使用openpyxl库自动调整列宽，以及如何使用 Pandas 的Styler对象设置背景色和字体格式，以确保数据在 Excel 文件中清晰展示。希望这篇文章能帮助你更高效地处理和导出数据到 Excel 文件中。如果你有任何问题或需要进一步的帮助，请随时告诉我。
Java读Excel：解析阿里云easyExcel导入文件的行号
专注于计算机研发知识和资讯分享
04-28 167
解析阿里云easyExcel导入文件的行号的应用场景： 提示哪行存在问题，例如不能为空，格式不符合，主键不存在等。导入类型、 是否限制导入数量、最大导入数量、其他的上下文数据inputData、存储回调方法的对象。默认所有字段都会和excel去匹配，加了这个注解会忽略该字段。所表示的类或接口相同，或是否是它的超类或超接口。对象所表示的类或接口是否与指定的。
2025A卷-正整数到Excel编号之间的转换
tu123456s的博客
04-28 234
用过 excel 的都知道excel的列编号是这样的：分别代表以下编号：1 2 3 … 26 27 28 29 … 52 53 54 55 … 676 677 678 679 … 702 703 704 705 … 请写个函数，完成从一个正整数到这种字符串之间的转换。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值