内点法最优潮流matlab程序

内点法最优潮流matlab程序
一、概述最优潮流问题
1.最优潮流和基本潮流的比较潮流计算可以归结为针对一定的扰动变量p(负荷情况)，根据给定的控制变量u(如发电机的有功出力、无功出力或节点电压模值等)，求出相应的状态变量x(如节点电压模值及角度)，这样通过一次潮流计算得到的潮流解决定了电力系统的一个运行状态。这种潮流计算也可以称之为基本潮流(或常规潮流)计算，一次基本潮流计算的结果主要满足了潮流方程式或变量间等式约束条件

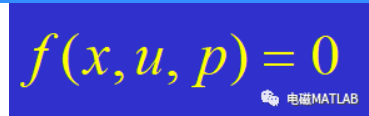
一次潮流计算所决定的运行状态可能由于某些状态变量或者作为u,x 函数的其它变量在数值上超出了它们所容许的运行限值(即不满足不等式约束条件)，因而在技术上并不是可行的。工程实际上常用的方法是调整某些控制变量的给定值，重新进行前述的基本潮流计算，这样反复进行，直到所有的约束条件都能够得到满足为止。这样便得到了一个技术上可行的潮流解。

由于系统的状态变量及有关函数变量的上下限值间有一定的间距，控制变量也可以在其一定的容许范围内调节，因而对某一种负荷情况，理论上可以同时存在为数众多的、技术上都能满足要求的可行潮流解。每一个可行潮流解对应于系统的某一个特定的运行方式，具有相应总体的经济上或技术上的性能指标(如系统总的燃料消耗量、系统总的网损等)，为了优化系统的运行，就有需要从所有的可行潮流解中挑选出上述性能指标为最佳的一个方案。而这就是本节要讨论的最优潮流所要解决的问题。

因此所谓最优潮流，就是当系统的结构参数及负荷情况给定时，通过控制变量的优选，所找到的能满足所有指定的约束条件，并使系统的某一个性能指标或目标函数达到最优时的潮流分布。

综上所述，最优潮流和基本潮流比较，有以下不同点：
(1)基本潮流计算时控制变量u是事先给定的；而最优潮流中的u则是可变而待优选的变量，为此在最优潮流模型中必然有一个作为u优选准则的目标函数。
(2)最优潮流计算除了满足潮流方程这一等式约束条件之外，还必须满足与运行限制有关的大量不等式约束条件。
(3)进行基本潮流计算是求解非线性代数方程组；而最优潮流计算由于其模型从数学上讲是一个非线性规划问题，因此需要采用最优化方法来求解。
(4)基本潮流计算所完成的仅仅是一种计算功能，即从给定的u求出相应的x