机器学习——子空间学习（PCA & LDA）

1. 引入：子空间学习与降维

什么是子空间学习？

• 子空间学习大意是指通过投影，实现高维特征向低维空间的映射，是一种经典的降维思想。绝大多数的维数约简（降维，投影）算法都算是子空间学习，如PCA、LDA、LPP、LLE等；
• 本文只介绍前两种维数约减算法，即主成分分析（PCA）和线性判别分析（LDA）。

什么是降维？什么情况下需要降维？

• 降维：寻找一组映射对样本进行重新表示（representation）；
• 原样本：$x=[x_1;x_2;...;x_d]\in {\mathbb{R}}^d$；新表示：$y=[y_1;y_2;...;y_m]\in {\mathbb{R}}^m(m<d)$；降维目标：学习映射$\varphi (x)=y$；
• 我们知道，样本空间是由样本的各个属性张成的空间，假设每个样本有$d$个属性，则样本空间就是一个$d$维空间，$d$维空间中的每个点就是一个样本的表示（representation）；
• 降维就是学习一个从原样本空间到新样本空间（子空间，即维度小于$d$，假设为$m$维）的映射，使得新样本空间中每个点是一个样本的新的表示，也就是说，每个样本的表示从$d$维向量简化为了$m$维向量，这显然是一件好事。

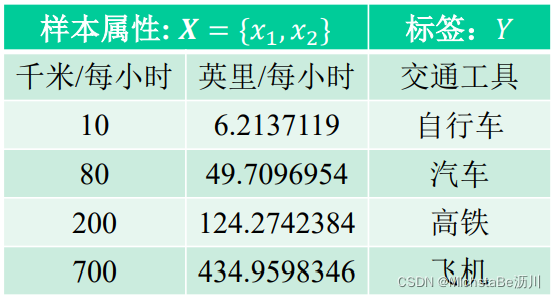
需要降维的情况：如数据冗余。下图中前两列表达的是同一个意思，造成了数据冗余，对此，应当进行降维。

数据冗余的弊端？维度灾难！

• 增加计算机开销（存储空间、计算资源）；
• 采样困难。

2. 主成分分析（PCA）

假设：映射$\varphi (\cdot )$是线性映射，线性映射的实质就是定义了一个新坐标。

$\varphi (\cdot ):W^{T}x=y\in {\mathbb{R}}^m,W=[w_1,w_2,...,w_m]\in {\mathbb{R}}^{d\times m}$

最大方差理论： 在信号处理中认为信号具有较大的方差，噪声有较小的方差。 即新坐标系上数据方差应越大越好。

2.1 目标函数

在新坐标系下最大化数据新表征的方差：$$\underset{w}{\max }\sum _{i=1}^n(y_i-\bar{y}{)}^2,$$$$\text{s.t.}{y}_i=w^T{x}_i,||w||=1.$$第二个约束条件是为了坐标系标准化。矩阵化表示：$$\underset{W}{\max }\sum _{i=1}^n||y_i-\bar{y}|{|}^2,$$$$\text{s.t.}{y}_i=W^T{x}_i,W^{T}W=I.$$其中$W=[w_1,...,w_m]\in {\mathbb{R}}^{d\times m}$，第二个约束条件保证坐标系为标准正交坐标系，也可表示为$||w_i||=1,w_i^T{w}_j=0$。PCA降维的过程可以通过数据乘以矩阵来表示，因此是一个线性变换。

• 原样本：$x=[x_1;x_2;...;x_d]\in {\mathbb{R}}^d$
• 新表示：$y=[y_1;y_2;...;y_m]\in {\mathbb{R}}^m(m<d)$

PCA的目标函数推导：$$f(W)=\sum _{i=1}^n||y_i-\bar{y}|{|}^2=\sum _{i=1}^n(y_i-\bar{y}{)}^T(y_i-\bar{y})=\sum _{i=1}^{n}tr((y_i-\bar{y})(y_i-\bar{y}{)}^T)$$$$=tr(\sum _{i=1}^n(y_i-\bar{y})(y_i-\bar{y}{)}^T)=tr(\sum _{i=1}^n(W^T{x}_i-W^T\bar{x})(W^T{x}_i-W^T\bar{x}))$$$$=tr(\sum _{i=1}^n{W}^T(x_i-\bar{x})(x_i-\bar{x}{)}^{T}W)=tr(W^T(\sum _{i=1}^n(x_i-\bar{x})(x_i-\bar{x}{)}^T)W)$$$$=tr(W^T(X-\bar{X})(X-\bar{X}{)}^{T}W)=tr(W^T(n-1)cov(X)W)$$

综上，PCA的目标函数如下：$$f(W)=tr(W^T(X-\bar{X})(X-\bar{X}{)}^{T}W)$$

2.2 问题求解

优化目标：$$\underset{W}{\max }tr(W^T(X-\bar{X})(X-\bar{X}{)}^{T}W),$$$$\text{s.t.}{W}^{T}W=I$$
采用拉格朗日乘子法，目标转化为：$$\underset{W}{\min }\mathcal{L}(W,\lambda )=-tr(W^T(X-\bar{X})(X-\bar{X}{)}^{T}W)+tr(\lambda (W^{T}W-I))$$令$\frac{\partial \mathcal{L}}{\partial W}=0$，得：$$(X-\bar{X})(X-\bar{X}{)}^{T}W=\lambda W$$这是一个典型的特征值分解问题，即：$$CW=\lambda W,C=(X-\bar{X})(X-\bar{X}{)}^T$$对$(X-\bar{X})(X-\bar{X}{)}^T$进行特征值分解得：$$(X-\bar{X})(X-\bar{X}{)}^T=V\Lambda V^T$$其中$\Lambda =diag({\lambda }_1,{\lambda }_2,...,{\lambda }_d),V=[v_1,v_2,...,v_d]$，得到的${\lambda }_1,{\lambda }_2,...,{\lambda }_d$就是$C$的$d$个特征值，$V$是特征值对应特征向量构成的矩阵。

注意：$V$的每一列代表一个特征向量。

我们对特征值进行排序，取前$m$个最大特征值所对应的特征向量即组成了最优投影矩阵：$$W=[v_1,v_2,...,v_m]$$至此，我们就可以使用矩阵$W$对数据进行投影降维了。

2.3 主成分解

• 第一主成分包含了样本方差的最大方向；
• 第二主成分与第一主成分不相关（夹角90度），包含了剩余样本方差的最大方向；
• 前几个主成分包含了样本的绝大部分信息，以至于可以忽略后面的主成分。

2.4 子空间、基和嵌入

• 投影矩阵$W=[w_1,...,w_m]$是新的数据表征的坐标系集合，我们可以说$W$在样本空间中张了一个子空间；
• 向量$w_i$定义一个样本的主成分，也定义新坐标系中第$i$个坐标轴，称为$W$张成的子空间的一个基；
• $y_i=W^T{x}_i$是样本$x_i$在$W$张成的子空间中的一个低维嵌入。

2.5 算法流程

• 样本中心化：$A=X-\bar{X}$，其中$\bar{X}=[\bar{x},\bar{x},...,\bar{x}]\in {\mathbb{R}}^{d\times n}$；
• 计算协方差矩阵：$C=A{A}^T=(X-\bar{X})(X-\bar{X}{)}^T$；
• 特征值分解：$C=V\Lambda V^T$
• 根据特征值选取特征向量构建投影矩阵：$W=[v_1,v_2,...,v_m]$

注意：$W$对应$V$的前$m$列！（前提：特征值已排序！）

• 输入原样本投影至新子空间完成降维：$\tilde{Y}=W^{T}A$

使用奇异值分解（SVD）后：

• 样本中心化：$A=X-\bar{X}$，其中$\bar{X}=[\bar{x},\bar{x},...,\bar{x}]\in {\mathbb{R}}^{d\times n}$；
• 奇异值分解：$A=U\Sigma V^T$
• 根据奇异值选取奇异向量构建投影矩阵：$W=[u_1,u_2,...,u_m]$

注意：$W$对应$U$的前$m$列！（前提：奇异值已排序！）

• 输入原样本投影至新子空间完成降维：$\tilde{Y}=W^{T}A$

问题：$y$的维度如何确定？

• 固定值（分类问题设为类别数目-1）；
• 试错法（trial by error）；
• 设定特征值比重的阈值：$\underset{m}{\max }{\sum }_{i=1}^m{\lambda }_i/{\sum }_{i=1}^d{\lambda }_i\ge h$；
• 根据保留维度-精度的图像拐点（如下）。

2.6 小结

• 核心思想：寻找合适的正交投影矩阵$W$，使得投影后的样本$Y=W^{T}X$方差最大，也就是说在新的空间中保留的信息越多越好。
• 不足之处：存储、计算开销大；并未利用到监督信息。

如何改进？

• 减小存储、计算开销：奇异值分解（SVD）。$A=U\Sigma V^T$，其中$A\in {\mathbb{R}}^{d\times n},U\in {\mathbb{R}}^{d\times r},\Sigma \in {\mathbb{R}}^{r\times r},V\in {\mathbb{R}}^{n\times r}$，$U$和$V$都是正交矩阵，$U$中每个向量称为$A$的左奇异向量，$V$中每个向量称为$A$的右奇异向量，而$\Sigma$是一个对角方阵，且$r$等于$A$的秩。（更多请看这篇：求分解后的$U,\Sigma ,V$三个矩阵的方法）

• 利用监督信息：线性判别分析（LDA）。

3. 线性判别分析（LDA）

费希尔准则（Fisher Criteria）：同类样本应该尽量聚合在一起，而不同类样本之间应该尽量扩散。如下图，即使得红线尽可能短，蓝线尽可能长。

如何定义聚合程度和扩散程度？
其实方差就可以实现！方差大，既可以表示聚合程度小，也可以表示扩散程度大！

3.1 同类样本的聚合程度

一维情况下（方差）：$$s_w(c)=\sum _{i\in c}(y_i-{\mu }_c{)}^2$$其中$c\in [1,...,c,...,C]$，共$C$个类，${\mu }_c=\frac{1}{n_c}\sum _{i\in c}{y}_i$是$c$类样本的中心。
多维情况下（协方差矩阵）：$$s_w(c)=tr(\sum _{i\in c}(y_i-{\mu }_c)(y_i-{\mu }_c{)}^T)$$

3.2 类别之间的扩散程度

$$s_b=\sum _{c=1}^{C}tr(({\mu }_c-\mu )({\mu }_c-\mu {)}^T)$$其中${\mu }_c=\frac{1}{n_c}\sum _{i\in c}{y}_i$是$c$类样本中心，$\mu =\frac{1}{n}\sum _i{y}_i$是总样本中心。

3.3 目标函数

根据费希尔准则，$y$在一个理想的坐标系下应当满足：$$\forall c,s_w(c)\downarrow ,s_b\uparrow$$故目标函数构建如下：$$\min \frac{{\sum }_c{s}_w(c)}{s_b}$$假设低维嵌入$y$由$x$通过投影矩阵$W$投影到LDA子空间，即：$$y=W^{T}x,y\in {\mathbb{R}}^{m\times 1},x\in {\mathbb{R}}^{d\times 1},W\in {\mathbb{R}}^{d\times m}$$则目标函数变为：$$\underset{W}{\min }tr(\frac{W^T{S}_{w}W}{W^T{S}_{b}W})$$该目标函数是$S_w$和$S_b$的广义瑞利商。其中类内散度矩阵$S_w$和类间散度矩阵$S_b$定义如下：$$S_w=\sum _{c=1}^C\sum _{i\in c}(x_i-{\bar{x}}_c)(x_i-{\bar{x}}_c{)}^T\in {\mathbb{R}}^{d\times d}$$$$S_b=\sum _{c=1}^C{n}_c({\bar{x}}_c-\bar{x})({\bar{x}}_c-\bar{x}{)}^T\in {\mathbb{R}}^{d\times d}$$该目标函数的最优解有无穷多个，因为可以对$W$进行任意缩放。所以，我们可以认为该问题等价于：$$\underset{W}{\min }tr(W^T{S}_{w}W),\text{s.t.},W^T{S}_{b}W=I$$

3.4 问题求解

在PCA中已求解过类似问题，即构造拉格朗日函数求偏导，得到一个典型的特征值分解问题，故此处不再详述。

构造构造拉格朗日函数，并求偏导得到：$$S_b^{-1}{S}_{w}W=\lambda W$$同理，这也是一个特征值分解问题。

3.5 算法流程

• 计算各类样本中心和所有样本中心：$${\mu }_c=\frac{1}{n_c}\sum _{i\in c}{y}_i,\mu =\frac{1}{n}\sum _i{y}_i$$
• 计算类间散度矩阵和类内散度矩阵：$$S_w=\sum _{c=1}^C\sum _{i\in c}(x_i-{\bar{x}}_c)(x_i-{\bar{x}}_c{)}^T\in {\mathbb{R}}^{d\times d}$$$$S_b=\sum _{c=1}^C{n}_c({\bar{x}}_c-\bar{x})({\bar{x}}_c-\bar{x}{)}^T\in {\mathbb{R}}^{d\times d}$$
• 特征值分解：$S_b^{-1}{S}_{w}W=\lambda W$；
• 根据特征值选取特征向量构建投影矩阵：$W=[v_1,v_2,...,v_m]$；
• 输入原样本投影至新子空间完成降维：$Y=W^{T}X$

3.6 PCA vs LDA

思想上：

• PCA旨在寻找一组子坐标系（定义一个子空间）使得样本点的方差最大，即信息量保留最多；
• LDA旨在寻找一组子坐标系（定义一个子空间）使得样本点类内散度小，类间散度大（费希尔准则）。

监督性：

• PCA是无监督学习方法；
• LDA是有监督学习方法。

子空间学习（subspace learning）角度：

• 两者都属于线性子空间学习算法，因为都在样本空间定义了一个新的子坐标系（子空间），每个列向量定义了一个坐标轴；
• 目标都是学习一个投影矩阵$W$，使得样本在新坐标系上的表示具有相应特性；

降维（dimension reduction）角度：

• 两者都有降维的效果，坐标轴数目减少，维度减少。

特征提取（feature extraction）角度：

• 两者都起到了特征提取的作用，样本在新坐标系下的坐标就相当于样本的新特征（表征、表示）。

效率：PCA效率好于LDA。

4. 子空间学习的核化

想想：如果样本分布不是线性的，怎么办？
思路：把样本利用非线性映射投射到更高的维度（一般来说），使得在高维非线性空间，可以使用线性子空间学习进行数据分析。

然而，对于任意给定数据寻找合适的非线性映射$\varphi$是不现实的。
回顾一下，在支持向量机这篇文章中，我曾介绍过核方法（kernel trick），也就是我们定义核函数$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$，使得$\varphi$可以隐式地由核函数表示出来。只要满足Mercer条件（即核矩阵对称半正定）的函数就是核函数，因此核函数很容易找到，并且有了核函数后，内积的计算也变得十分方便。链接中的文章也介绍了常见的核函数。
在此，我们以PCA和LDA为例，对子空间学习进行核化。