1. 神经元模型
1.1 什么是神经网络?
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所做的交互反应。
神经网络中最基本的成分是神经元模型。
1.2 M-P神经元模型
神经元接收来自
n
n
n个其他神经元的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总加权输入值与神经元的阈值进行比较,然后通过激活函数处理以产生神经元的输出。

神经元状态:
- 当 ∑ i = 1 n w i x i ≥ θ \sum\limits_{i=1}^nw_ix_i≥\theta i=1∑nwixi≥θ时,神经元被激活,处在兴奋状态,假设其对应输出为 y = 1 y=1 y=1;
- 当 ∑ i = 1 n w i x i < θ \sum\limits_{i=1}^nw_ix_i<\theta i=1∑nwixi<θ时,神经元未被激活,处在抑制状态,假设其对应输出为 y = 0 y=0 y=0。
激活函数 f ( ⋅ ) f(·) f(⋅):
- 激活函数将连续空间 [ − ∞ , + ∞ ] [-∞,+∞] [−∞,+∞]映射到离散空间 [ 0 , 1 ] [0,1] [0,1];
- 理想激活函数是阶跃函数(0表示抑制神经元,1表示激活神经元),但阶跃函数具有不连续、不光滑等不好的性质, 常用的是Sigmoid函数。

注意:
- 神经元模型与逻辑回归模型求解的优化问题是一致的,都是线性二分类问题,也就是说在本质上,M-P神经元 = 线性二分类器。进一步, y = f ( ∑ i = 1 n w i x i − θ ) y=f(\sum\limits_{i=1}^nw_ix_i-\theta) y=f(i=1∑nwixi−θ)可表示为 y = f ( w ^ T x ^ ) y=f(\hat{w}^T\hat{x}) y=f(w^Tx^);
- Sigmoid函数 ≠ Logistic函数,后者是前者的子集。

2. 感知机与多层网络
2.1 感知机(Perceptron)
感知机是最简单的神经网络,由两层组成:
- 输入层:接收外界信号,可以有多个信号;
- 输出层:M-P神经元,也称为阈值逻辑单元。

优化目标:最小化所有误分类点到分类超平面的距离之和。
- 令 w 0 = θ w_0=\theta w0=θ,则: ∑ i = 1 n w i x i − θ = ∑ i = 1 n w i x i − w 0 = w ^ T x ^ \sum\limits_{i=1}^nw_ix_i-\theta=\sum\limits_{i=1}^nw_ix_i-w_0=\hat{w}^T\hat{x} i=1∑nwixi−θ=i=1∑nwixi−w0=w^Tx^。其中, w ^ = [ w 0 ; w 1 ; . . . ; w n ] , x ^ = [ − 1 ; x 1 ; . . . ; x n ] \hat{w}=[w_0;w_1;...;w_n],\hat{x}=[-1;x_1;...;x_n] w^=[w0;w1;...;wn],x^=[−1;x1;...;xn];
- 点到超平面的距离为: d i s t ( x ^ , w ^ ) = ∣ w ^ T x ^ ∣ ∣ ∣ w ∣ ∣ 2 dist(\hat{x},\hat{w})=\frac{|\hat{w}^T\hat{x}|}{||w||_2} dist(x^,w^)=∣∣w∣∣2∣w^Tx^∣,其中 ∣ ∣ w ∣ ∣ 2 = ∑ i = 1 n w i 2 ||w||_2=\sqrt{\sum\limits_{i=1}^nw_i^2} ∣∣w∣∣2=i=1∑nwi2;
- x ^ \hat{x} x^的真实标签是 y y y,通过感知机的预测标签为 y ^ = f ( w ^ T x ^ ) \hat{y}=f(\hat{w}^T\hat{x}) y^=f(w^Tx^)。
对于 y y y和 y ^ \hat{y} y^进一步讨论如下:
- 若 y = 0 y=0 y=0被预测为 y ^ = 1 \hat{y}=1 y^=1,则 w ^ T x ^ > 0 \hat{w}^T\hat{x}>0 w^Tx^>0且 y ^ − y = 1 \hat{y}-y=1 y^−y=1,因此 ∣ w ^ T x ^ ∣ ∣ ∣ w ∣ ∣ 2 = ( y ^ − y ) w ^ T x ^ ∣ ∣ w ∣ ∣ 2 \frac{|\hat{w}^T\hat{x}|}{||w||_2}=(\hat{y}-y)\frac{\hat{w}^T\hat{x}}{||w||_2} ∣∣w∣∣2∣w^Tx^∣=(y^−y)∣∣w∣∣2w^Tx^;
- 若 y = 1 y=1 y=1被预测为 y ^ = 0 \hat{y}=0 y^=0,则 w ^ T x ^ < 0 \hat{w}^T\hat{x}<0 w^Tx^<0且 y ^ − y = − 1 \hat{y}-y=-1 y^−y=−1,因此 ∣ w ^ T x ^ ∣ ∣ ∣ w ∣ ∣ 2 = ( y ^ − y ) w ^ T x ^ ∣ ∣ w ∣ ∣ 2 \frac{|\hat{w}^T\hat{x}|}{||w||_2}=(\hat{y}-y)\frac{\hat{w}^T\hat{x}}{||w||_2} ∣∣w∣∣2∣w^Tx^∣=(y^−y)∣∣w∣∣2w^Tx^。
综上, d i s t ( x ^ , w ^ ) = ( y ^ − y ) w ^ T x ^ ∣ ∣ w ∣ ∣ 2 dist(\hat{x},\hat{w})=(\hat{y}-y)\frac{\hat{w}^T\hat{x}}{||w||_2} dist(x^,w^)=(y^−y)∣∣w∣∣2w^Tx^。
目标函数:
min
∑
t
∈
M
∣
w
^
T
x
t
^
∣
∣
∣
w
∣
∣
2
=
∑
t
(
y
t
^
−
y
t
)
w
^
T
x
t
^
∣
∣
w
∣
∣
2
\min\sum\limits_{t∈M}\frac{|\hat{w}^T\hat{x_t}|}{||w||_2}=\sum\limits_t(\hat{y_t}-y_t)\frac{\hat{w}^T\hat{x_t}}{||w||_2}
mint∈M∑∣∣w∣∣2∣w^Txt^∣=t∑(yt^−yt)∣∣w∣∣2w^Txt^
min
J
(
w
^
)
=
∑
t
(
y
t
^
−
y
t
)
w
^
T
x
t
^
\min J({\hat{w}})=\sum\limits_t(\hat{y_t}-y_t)\hat{w}^T\hat{x_t}
minJ(w^)=t∑(yt^−yt)w^Txt^其中,
(
y
t
^
−
y
t
)
w
^
T
x
t
^
∣
∣
w
∣
∣
2
(\hat{y_t}-y_t)\frac{\hat{w}^T\hat{x_t}}{||w||_2}
(yt^−yt)∣∣w∣∣2w^Txt^称为几何间隔,
(
y
t
^
−
y
t
)
w
^
T
x
t
^
(\hat{y_t}-y_t)\hat{w}^T\hat{x_t}
(yt^−yt)w^Txt^称为函数间隔,因此感知机的目标是最小化几何间隔或函数间隔。无论最小化哪个间隔,都可以达到优化目标,由于函数间隔相对简单,一般采用函数间隔。
标准梯度下降法:沿所有样本的平均梯度方向下降。
w
^
←
w
^
−
η
∑
t
(
y
t
^
−
y
t
)
x
t
^
\hat{w}←\hat{w}-\eta\sum\limits_t(\hat{y_t}-y_t)\hat{x_t}
w^←w^−ηt∑(yt^−yt)xt^随机梯度下降法:随机选取一个样本,沿其梯度下降方向更新。
w
^
←
w
^
−
η
(
y
^
−
y
)
x
^
\hat{w}←\hat{w}-\eta(\hat{y}-y)\hat{x}
w^←w^−η(y^−y)x^
标准梯度下降法 vs 随机梯度下降法:
- 一般而言,标准梯度下降的 η \eta η比随机梯度下降的大。因为标准梯度下降使用“准确”的梯度,而随机梯度下降使用“近似”的梯度;
- 当 J ( w ^ ) J(\hat{w}) J(w^)有多个局部极小值时,随机梯度下降反而更可能避免陷入局部极小值;
- 标准梯度下降在更新参数时要遍历整个数据集,当数据量很大时,1)收敛很慢;2)不能保证找到全局最小值。
单层感知机特性:
-
能够解决线性可分的情况(如与、或、非运算)
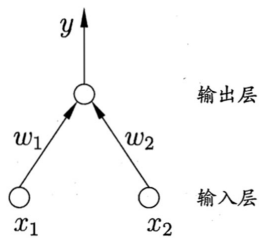
- 与:令 w 1 = w 2 = 1 , θ = 2 w_1=w_2=1,\theta=2 w1=w2=1,θ=2,则 y = f ( 1 ⋅ x 1 + 1 ⋅ x 2 − 2 ) y=f(1·x_1+1·x_2-2) y=f(1⋅x1+1⋅x2−2),仅在 x 1 = x 2 = 1 x_1=x_2=1 x1=x2=1时, y = 1 y=1 y=1;
- 或:令 w 1 = w 2 = 1 , θ = 0.5 w_1=w_2=1,\theta=0.5 w1=w2=1,θ=0.5,则 y = f ( 1 ⋅ x 1 + 1 ⋅ x 2 − 0.5 ) y=f(1·x_1+1·x_2-0.5) y=f(1⋅x1+1⋅x2−0.5),当 x 1 = 1 x_1=1 x1=1或 x 2 = 1 x_2=1 x2=1时, y = 1 y=1 y=1;
- 非:令 w 1 = − 0.6 , w 2 = 0 , θ = − 0.5 w_1=-0.6,w_2=0,\theta=-0.5 w1=−0.6,w2=0,θ=−0.5,则 y = f ( − 0.6 ⋅ x 1 + 0 ⋅ x 2 + 0.5 ) y=f(-0.6·x_1+0·x_2+0.5) y=f(−0.6⋅x1+0⋅x2+0.5),当 x 1 = 1 x_1=1 x1=1时, y = 0 y=0 y=0;当 x 1 = 0 x_1=0 x1=0时, y = 1 y=1 y=1。
-
不能解决线性不可分的情况(如异或运算)
- 需要引入多层网络。
2.2 多层网络
为了解决非线性可分问题,需要引入多层网络。
- 多层网络:包含隐层的网络;
- 前馈网络:神经元之间不存在同层连接也不存在跨层连接;
- 多层前馈神经网络:具有层级结构的前馈网络;
- 隐层和输出层神经元亦称“功能单元”。
注意:由于输入层神经元只接受输入信号,而不进行函数处理,因此输入层一般不记入网络层数中。

3. 误差逆传播算法
3.1 算法推导与伪代码
最成功、最常用的神经网络算法,可被用于多种任务(不仅限于分类)。
- 训练集: D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , x i ∈ R d , y i ∈ R l D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\},x_i∈\mathbb{R}^d,y_i∈\mathbb{R}^l D={(x1,y1),(x2,y2),...,(xm,ym)},xi∈Rd,yi∈Rl;
- 输入: d d d维特征向量 x i ∈ R d x_i∈\mathbb{R}^d xi∈Rd;
- 输出: l l l个输出值 y i ∈ R l y_i∈\mathbb{R}^l yi∈Rl;
- 隐层: q q q个隐层神经元;
- 假设:功能单元(隐层和输出层神经元)都使用Sigmoid激活函数。

对于给定样例
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk),假定网络的实际输出为
y
^
k
=
(
y
^
1
k
,
y
^
2
k
,
.
.
.
,
y
^
l
k
)
\hat{y}^k=(\hat{y}_1^k,\hat{y}_2^k,...,\hat{y}_l^k)
y^k=(y^1k,y^2k,...,y^lk),而
y
^
j
k
=
f
(
β
j
−
θ
j
)
\hat{y}_j^k=f(\beta_j-\theta_j)
y^jk=f(βj−θj),则网络在
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk)上的均方误差为:
E
k
=
1
2
∑
j
=
1
l
(
y
^
j
k
−
y
j
k
)
2
E_k=\frac{1}{2}\sum\limits_{j=1}^l(\hat{y}_j^k-y_j^k)^2
Ek=21j=1∑l(y^jk−yjk)2其中需要学习的参数有
(
d
+
l
+
1
)
q
+
l
(d+l+1)q+l
(d+l+1)q+l个。
- 隐藏层神经元到每个输入层神经元的权重,共有 d × q d×q d×q个;
- 输出层神经元到每个隐藏层神经元的权重,共有 l × q l×q l×q个;
- 每个功能单元有一个阈值,隐藏层和输出层分别有 q q q个和 l l l个。
又是一个小细节:为什么均方误差系数是 1 2 \frac{1}{2} 21呢?因为系数是个常数,随便取多少都不会影响优化目标。取 1 2 \frac{1}{2} 21当然是因为方便求导(求梯度),因为后面有个平方项,求导后刚好约掉了!
BP 算法基于梯度下降策略,以目标的负梯度方向对参数进行调整。
例如对于
w
h
j
w_{hj}
whj,容易得到:
Δ
w
h
j
=
−
η
∂
E
k
∂
w
h
j
\Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}}
Δwhj=−η∂whj∂Ek我们已经知道:
β
j
=
∑
h
=
1
q
w
h
j
b
h
\beta_j=\sum\limits_{h=1}^qw_{hj}b_h
βj=h=1∑qwhjbh
y
^
j
k
=
f
(
β
j
−
θ
j
)
\hat{y}_j^k=f(\beta_j-\theta_j)
y^jk=f(βj−θj)
E
k
=
1
2
∑
j
=
1
l
(
y
^
j
k
−
y
j
k
)
2
E_k=\frac{1}{2}\sum\limits_{j=1}^l(\hat{y}_j^k-y_j^k)^2
Ek=21j=1∑l(y^jk−yjk)2注意到
w
h
j
w_{hj}
whj先影响到
β
j
\beta_j
βj,再影响到
y
^
j
k
\hat{y}_j^k
y^jk,最后才影响到
E
k
E_k
Ek,故由链式法则知:
∂
E
k
∂
w
h
j
=
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
⋅
∂
β
j
∂
w
h
j
\frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat{y}_j^k}·\frac{\partial \hat{y}_j^k}{\partial \beta_j}·\frac{\partial \beta_j}{\partial w_{hj}}
∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj对三个偏导数计算如下:
∂
β
j
∂
w
h
j
=
b
h
\frac{\partial \beta_j}{\partial w_{hj}}=b_h
∂whj∂βj=bh
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
=
(
y
^
j
k
−
y
j
k
)
f
′
(
β
j
−
θ
j
)
=
y
^
j
k
(
1
−
y
^
j
k
)
(
y
^
j
k
−
y
j
k
)
\frac{\partial E_k}{\partial \hat{y}_j^k}·\frac{\partial \hat{y}_j^k}{\partial \beta_j}=(\hat{y}_j^k-y_j^k)f'(\beta_j-\theta_j)=\hat{y}_j^k(1-\hat{y}_j^k)(\hat{y}_j^k-y_j^k)
∂y^jk∂Ek⋅∂βj∂y^jk=(y^jk−yjk)f′(βj−θj)=y^jk(1−y^jk)(y^jk−yjk)
上面没看懂?我来给你答疑解惑!我们知道Sigmoid函数的表达式为: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1,并且其具有良好的性质,什么性质呢?就是 f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x)),我们又知道 f ( β j − θ j ) = y ^ j k f(\beta_j-\theta_j)=\hat{y}_j^k f(βj−θj)=y^jk所以不难得到 f ′ ( β j − θ j ) = y ^ j k ( 1 − y ^ j k ) f'(\beta_j-\theta_j)=\hat{y}_j^k(1-\hat{y}_j^k) f′(βj−θj)=y^jk(1−y^jk)
我们令:
g
j
=
−
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
=
y
^
j
k
(
1
−
y
^
j
k
)
(
y
j
k
−
y
^
j
k
)
g_j=-\frac{\partial E_k}{\partial \hat{y}_j^k}·\frac{\partial \hat{y}_j^k}{\partial \beta_j}=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k)
gj=−∂y^jk∂Ek⋅∂βj∂y^jk=y^jk(1−y^jk)(yjk−y^jk)得到:
Δ
w
h
j
=
−
η
∂
E
k
∂
w
h
j
=
η
g
j
b
h
\Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}}=\eta g_jb_h
Δwhj=−η∂whj∂Ek=ηgjbh
同理,我们得到:
- Δ w h j = η g j b h \Delta w_{hj}=\eta g_jb_h Δwhj=ηgjbh
- Δ v i h = η e h x i \Delta v_{ih}=\eta e_hx_i Δvih=ηehxi
- Δ θ j = − η g j \Delta \theta_j=-\eta g_j Δθj=−ηgj
- Δ γ h = − η e h \Delta \gamma_h=-\eta e_h Δγh=−ηeh
其中,
g
j
=
y
^
j
k
(
1
−
y
^
j
k
)
(
y
j
k
−
y
^
j
k
)
g_j=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k)
gj=y^jk(1−y^jk)(yjk−y^jk),
e
h
=
b
h
(
1
−
b
h
)
∑
j
=
1
l
w
h
j
g
j
e_h=b_h(1-b_h)\sum\limits_{j=1}^lw_{hj}g_j
eh=bh(1−bh)j=1∑lwhjgj。
于是,我们得到每次迭代的参数更新法则:
- w h j ← w h j + η g j b h w_{hj}←w_{hj}+\eta g_jb_h whj←whj+ηgjbh
- v i h ← v i h + η e h x i v_{ih}←v_{ih}+\eta e_hx_i vih←vih+ηehxi
- θ j ← θ j − η g j \theta_j←\theta_j-\eta g_j θj←θj−ηgj
- γ h ← γ h − η e h \gamma_h←\gamma_h-\eta e_h γh←γh−ηeh
算法伪代码:

3.2 标准BP算法 vs 累积BP算法
- 标准BP算法:如上,每次仅针对一个训练样例更新权值和阈值,也就是基于单个 E k E_k Ek推导而得;
- 累积BP算法:类似地,推导出基于累积误差最小化的更新规则,就是累积BP算法。
累积BP算法的目标:最小化训练集 D D D上的累积误差。 min E = 1 m ∑ k = 1 m E k \min E=\frac{1}{m}\sum\limits_{k=1}^mE_k minE=m1k=1∑mEk两者比较:
- 标准BP算法:每次针对单个训练样例更新权值和阈值;参数更新频繁,不同样例可能抵消,需要多次迭代;
- 累积BP算法:其优化目标是最小化整个训练集上的累积误差;读取整个训练集一遍才对参数进行更新,参数更新频率较低;
- 在很多任务中,当累积误差下降到一定程度后,进一步下降会非常缓慢,这时标准BP算法往往会获得较好的解,尤其当训练集非常大时效果更明显。
3.3 防止过拟合
3.3.1 早停
- 若训练误差连续a轮的变化小于b,则停止训练;
- 使用验证集:若训练误差降低、验证误差升高,则停止训练。
3.3.2 正则化
- 在误差目标函数中增加一项(正则项)以描述网络复杂度。
例如,将累积BP算法的误差目标函数修正为: E = λ 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i w i 2 E=\lambda \frac{1}{m}\sum\limits_{k=1}^mE_k+(1-\lambda)\sum\limits_iw_i^2 E=λm1k=1∑mEk+(1−λ)i∑wi2其中正则项为 ( 1 − λ ) ∑ i w i 2 (1-\lambda)\sum\limits_iw_i^2 (1−λ)i∑wi2,该正则项会偏好比较小的连接权和阈值,使网络输出更“光滑”;而 λ ∈ ( 0 , 1 ) \lambda∈(0,1) λ∈(0,1)用于对经验误差与网络复杂度进行折中,常通过交叉验证法来估计。
3.4 全局最小 vs 局部极小
- 神经网络的训练过程可看作一个参数寻优过程:即在参数空间中,寻找一组最优参数使得误差最小。
- 基于梯度的搜索是使用最广泛的参数寻优方法,例如梯度下降法。
- 如果误差函数仅有一个局部极小,那么找到它就找到了全局最小;但如果有多个,就不能保证了。
跳出局部极小的方法:
- 不同的初始参数:以多组不同参数值初始化多个神经网络,按照标准方法训练后,取其中误差最小的解作为最终参数;
- 模拟退火:在每一步都以一定的概率接受比当前解更差的结果;
- 随机扰动:例如随机梯度下降在计算梯度时加入了随机因素(每次迭代随机选取一个样本);
- 遗传算法
注意:上述技术大多是启发式的,说白了就是没有理论保障的,慎用。
4. 其他常见神经网络

4.1 RBF网络(径向基函数网络)

补充:
- x x x是 d d d维输入向量, q q q是隐层神经元个数, c i c_i ci和 w i w_i wi分别是第 i i i个神经元对应的中心和权重, ρ ( x , c i ) \rho(x,c_i) ρ(x,ci)是径向基函数。
- 径向基函数是某种沿径向对称的标量函数,通常定义为样本 x x x到数据中心 c i c_i ci之间欧氏距离的单调函数。高斯径向基函数是常用的径向基函数。
4.2 级联相关网络
- 构造性神经网络,也称为结构自适应神经网络(定义如下);
- 级联相关网络是构造性神经网络的代表。
级联相关网络有两个主要成分:
- 级联:建立层次连接的层级结构;
- 相关:通过最大化新结点的输出与网络误差之间的相关性来训练参数。
与一般的前馈神经网络相比,级联相关网络无需设置网络层数、隐层神经元数目,且训练速度快,但其在数据较小时易陷入过拟合。

4.3 Elman网络
Elman网络是递归神经网络的代表。























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








