论文导读 | 图对齐

论文导读 | 图对齐

半监督图对齐

图对齐问题是将两个图的节点进行匹配的问题。而半监督图对齐指的是已知小部分节点之间的对应关系，通过学习获得其他节点的匹配关系。

问题定义如下：给定属性图 G 1 = { A 1 , X 1 } G_1 = \{A_1,X_1\} G1​={A1​,X1​}、 G 2 = { A 2 , X 2 } G_2 = \{A_2,X_2\} G2​={A2​,X2​}和锚节点对，输出相似矩阵$S$，$S(x,a)$表示$G_1$中结点$a$和$G_2$中结点$x$​的相似性。

解决这个问题常见方法有以下3种：consistency-based、embedding-based和optimal transport。

consistency-based method

consistency-based method基于拓扑结构的一致性假设，即如果在图$G_1$中$a$和$b$是相邻节点，在图$G_2$中$x$和$y$也是相邻节点，并且如果$a$对齐到$x$，那么很可能$b$应该对齐到$y$​​。目标函数如下：

$ O_ {c} (S)= \alpha
\sum _ {a,b,x,y} [\frac {S(x,a)}{\sqrt {d_ {2}(x)d_ {1}(a)}}-\frac {S(y,b)}{\sqrt {d_ {2}(y)d_ {1}(b)}}]^ {2} A_ {1} (a,b) A_ {2} (x,y)
+(1- \alpha )\parallel S- H\parallel_ {F}^ {2} $

其中$d(\bullet )$为结点的度数；$H$是先验对齐矩阵，有锚链接的条目为1，否则为0。

目标函数的显式解为$\mathbf{s}(i)=(1-\alpha ){\sum }_{j=0}^{n_2\times n_1-1}{\sum }_{t=0}^{\infty }{\alpha }^t{\hat{\mathbf{W}}}^t(i,j)1(\mathbf{h}(j))$​

其中，$\hat{\mathbf{W}}={\mathrm{D}}_{\mathrm{W}}^{-\frac{1}{2}}{\mathbf{WD}}_{\mathrm{W}}^{-\frac{1}{2}}$并且$\mathbf{W}={\mathbf{A}}_1\otimes {\mathbf{A}}_2$。所以${\hat{\mathbf{W}}}^t(i,j)1(\mathbf{h}(j))$表示锚点对$j$经过$t$步移动到$i$。$\mathbf{s}(i)$是锚点对在product graph随机游走，以$\alpha$​概率消减赋值，得到的和。

consistency-based方法有以下两个局限性：

一、然而，由于网络的异质性，这种一致性假设很可能会被违反。例如，用户可能在一个社交网络中表现活跃，而在另一个社交网络中表现安静。上述公式要求，只有当锚链的两个锚节点以完全相同的步长$t$到达给定节点对时，才能给结点对赋值。所以即使是很小的扰动也可能对结果产生巨大的影响。

二、上述公式可能产生过平滑的问题。

embedding-based

BRIGHT[1]模型在consistency-based方法的基础上获得结点embedding。BRIGHT使用RWR算法求得$R_1$embedding矩阵，公式为${\mathbf{r}}_{l_1}=(1-\beta ){\hat{\mathbf{W}}}_1{\mathbf{r}}_{l_1}+\beta {\mathbf{e}}_{l_1}$。这样避免了步长相同的限制，给随机行走过程带来了更大的灵活性，更具鲁棒性。然后经过线性层获得拓扑结构相关的node embedding，这是为了让两个图嵌入到同一个空间。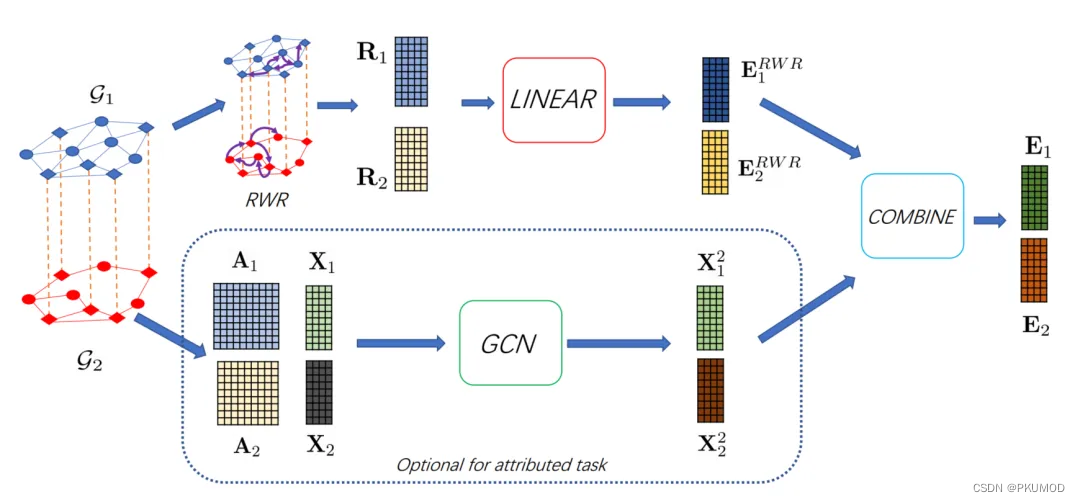

BRIGHT使用marginal ranking loss， J i = 1 ∣ L ∣ ∑ l ∈ L 1 ∣ U l i ∣ ∑ u ∈ U l i max ⁡ { 0 , γ + d ( l 1 , l 2 ) − d ( l i , u ) } \mathcal{J}_i=\frac{1}{|\mathcal{L}|} \sum_{l \in \mathcal{L}} \frac{1}{\left|U_{l_i}\right|} \sum_{u \in U_{l_i}} \max \left\{0, \gamma+d\left(l_1, l_2\right)-d\left(l_i, u\right)\right\} Ji​=∣L∣1​∑l∈L​∣Uli​​∣1​∑u∈Uli​​​max{0,γ+d(l1​,l2​)−d(li​,u)}。其中$U_{l_i}$是节点$l_i$的负对抽样集。为了提高负采样的质量和对齐性能，我们采样$G_2$中与锚节点$l_1$在$G_1$中的嵌入最接近的节点作为下一个epoch的负样例。

---

NextAlign[2]在建模结点embedding和采样两个方面对BRIGHT做出改进。

NextAlign在RWR和线性层中间增加了RelGCN-U和注意力机制。RelGCN-U是合并两个图并在大图上进行消息传递，这是为了更好地建模两个图之间的交互关系。注意力机制是为了解决区域之间对齐分数一致的过平滑问题（例如图中的点$g$和点$f$）。

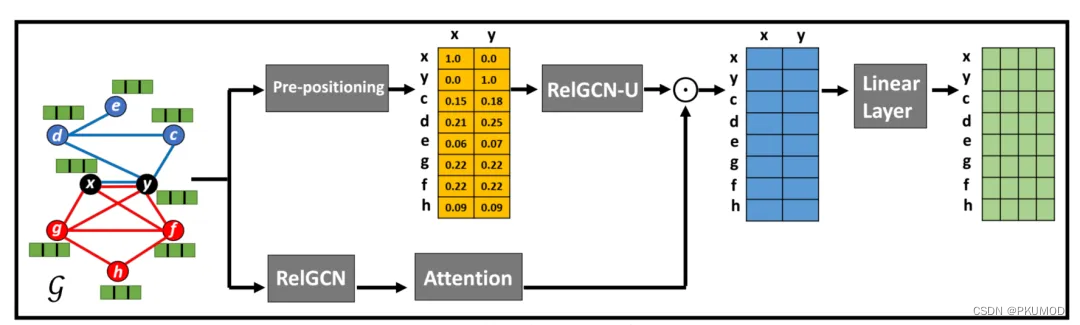
损失函数如下：

$\begin{array}{rl}{J}_a& =-\sum _b\left[p_d(b\mid a)\log \sigma \left({\mathbf{b}}^{\prime }\mathbf{a}\right)+k{p}_n(b\mid a)\log \sigma \left(-{\mathbf{b}}^{\prime }\mathbf{a}\right)\right]\\ J_x& =-\sum _y\left[p_d(y\mid x)\log \sigma \left({\mathbf{y}}^{\prime }\mathbf{x}\right)+k{p}_n(y\mid x)\log \sigma \left(-{\mathbf{y}}^{\prime }\mathbf{x}\right)\right]\\ J_{ax}& =-\sum _b\left[p_{dc}(b\mid x)\log \sigma \left({\mathbf{b}}^{\prime }\mathbf{x}\right)+k{p}_{nc}(b\mid x)\log \sigma \left(-{\mathbf{b}}^{\prime }\mathbf{x}\right)\right]\\ & -\sum _y\left[p_{dc}(y\mid a)\log \sigma \left({\mathbf{y}}^{\prime }\mathbf{a}\right)+k{p}_{nc}(y\mid a)\log \sigma \left(-{\mathbf{y}}^{\prime }\mathbf{a}\right)\right]\\ J& =\sum _{(a,x)\in \mathcal{L}}{J}_{(a,x)}=\sum _{(a,\mathbf{x})\in \mathcal{L}}{J}_a+J_x+J_{ax}\end{array}$

在抽样负样本$p_{nc}$​​​的时候，一些方法主张抽样embedding相近的结点，然而这违反对齐一致性假设；另一些方法主张抽样embedding相差较大的结点或者随机采样，这可能对学习有意义的嵌入贡献不大。

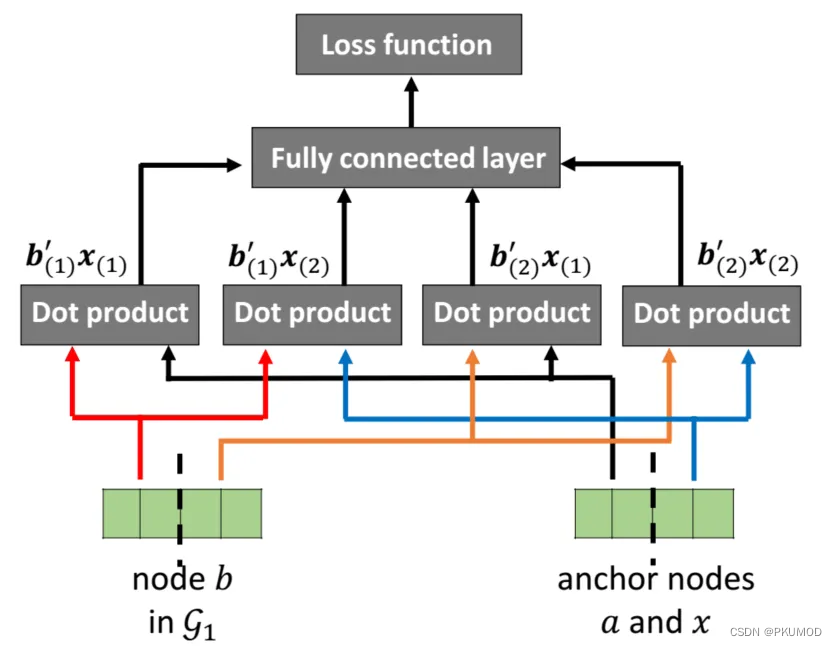
NextAlign为了解决这个问题，就将embedding分为两块，一块表示在本图的信息，一块表示在另一张图中的信息。在采样的时候使用不同部分的信息。公式如下：

$\begin{array}{rl}{p}_d(b\mid a)& =\frac{\sigma \left({\mathbf{b}}_{(1)}^{\prime }{\mathbf{x}}_{(1)}\right)}{{\sum }_{c\in {\mathcal{V}}_1}\sigma \left({\mathbf{c}}_{(1)}^{\prime }{\mathbf{x}}_{(1)}\right)}\\ p_n(b\mid a)& =\frac{\sigma \left(-{\mathbf{b}}_{(1)}^{\prime }{\mathbf{x}}_{(1)}\right)}{{\sum }_{c\in {\mathcal{V}}_1}\sigma \left(-{\mathbf{c}}_{(1)}^{\prime }{\mathbf{x}}_{(1)}\right)}\\ p_{dc}(b\mid x)& =\frac{\sigma \left({\mathbf{b}}_{(2)}^{\prime }{\mathbf{x}}_{(2)}\right)}{{\sum }_{c\in {\mathcal{V}}_1}\sigma \left({\mathbf{c}}_{(2)}^{\prime }{\mathbf{x}}_{(2)}\right)}\\ p_{nc}(b\mid x)& =\frac{\sigma \left({\mathbf{b}}_{(1)}^{\prime }{\mathbf{x}}_{(2)}+{\mathbf{b}}_{(2)}^{\prime }{\mathbf{x}}_{(1)}\right)}{{\sum }_{c\in {\mathcal{V}}_1}\sigma \left({\mathbf{c}}_{(1)}^{\prime }{\mathbf{x}}_{(2)}+{\mathbf{c}}_{(2)}^{\prime }{\mathbf{x}}_{(1)}\right)}\end{array}$

optimal transport

optimal transport把相似矩阵的计算建模为最优传输问题。
$\mathbf{S}=\underset{\mathbf{S}\in \Pi (\mathbf{\mu },\mathbf{v})}{\mathrm{argmin}}{\sum }_{x_i,y_j}\mathbf{C}\left(x_i,y_j\right)\mathbf{S}\left(x_i,y_j\right)=\underset{\mathbf{S}\in \Pi (\mathbf{\mu },\mathbf{v})}{\mathrm{argmin}}⟨\mathbf{C},\mathbf{S}⟩$​
$\mu =\frac{1_{n_1}}{n_1},\mathbf{v}=\frac{1_{n_2}}{n_2}$
其中$C$是代价矩阵，$S$是相似矩阵。

PARROT[3]除此之外，还设计了3个正则化项。

一、edge consistency regularization：两个对齐结点之间的连边embedding通常比较相似

$\begin{array}{rl}{L}_e& =\sum _{x,x^{\prime },y,y^{\prime }}{\mathbf{L}}_e\left(x,x^{\prime },y,y^{\prime }\right)\\ & =\sum _{\begin{array}{c}x,y\\ x^{\prime }\in \mathcal{N}(x),y^{\prime }\in \mathcal{N}(y)\end{array}}{\left|{\mathbf{C}}_1\left(x,x^{\prime }\right)-{\mathbf{C}}_2\left(y,y^{\prime }\right)\right|}^2\mathbf{S}(x,y)\mathbf{S}\left(x^{\prime },y^{\prime }\right)\end{array}$
$C_i$是边embedding矩阵，${\mathbf{C}}_i=e^{-{\mathbf{X}}_i{\mathbf{X}}_i^{\top }}\odot {\mathbf{A}}_i$

二、neighborhood consistency：相同邻域的相似度相近

$L_n=-⟨\log \hat{\mathbf{S}},\mathbf{S}⟩+⟨\log \mathbf{S},\mathbf{S}⟩$
其中$\hat{\mathbf{S}}$表示的是局部相似度信息

三、S和先验分布相近
$L_a=-⟨\log \mathbf{H},\mathrm{S}⟩+⟨\log \mathrm{S},\mathrm{S}⟩$
其中$H$是先验相似矩阵，$\mathbf{H}(x,y)=\frac{1}{|f|}$，当且仅当 $(x,y)\in \mathcal{L}$​。

最终的优化公式为${\min }_{\mathbf{S}\in \Pi (\mathbf{\mu },\mathbf{v})}f(\mathbf{S})=⟨\mathbf{C},\mathbf{S}⟩+{\lambda }_e{L}_e+{\lambda }_n{L}_n+{\lambda }_a{L}_a$。可以将其转化为凸优化问题并通过近似点算法进行求值。

Reference

[1] Yan, Y., Zhang, S., & Tong, H. (2021). BRIGHT: A Bridging Algorithm for Network Alignment. Proceedings of the Web Conference 2021.

[2] Zhang, S., Tong, H., Jin, L., Xia, Y., & Guo, Y. (2021). Balancing Consistency and Disparity in Network Alignment. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining.

[3] Zeng, Z., Zhang, S., Xia, Y., & Tong, H. (2023). PARROT: Position-Aware Regularized Optimal Transport for Network Alignment. Proceedings of the ACM Web Conference 2023.