关于小游戏魔塔的优化算法(1)---初窥自动寻路算法

魔塔小游戏介绍

魔塔是一类固定数值的RPG游戏，画面为（MxN）并且通过上下左右的方式游玩。

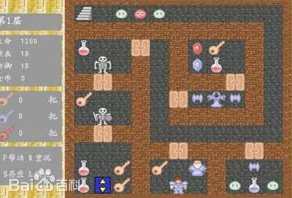
游戏地图地图可以转化为二维数组形式，
举个例子：
{
{0,0,1,0,0,0},
{5,1,0,0,1,1},
{1,0,0,1,0,1},
{1,1,0,1,0,1},
{0,1,0,0,9,0},
{0,0,0,1,0,1},
}
其中9为主角，0为路，1为墙（
因为是寻路，所以可以不考虑怪物，宝物，钥匙带来的影响，所以一律归为墙）

设计需求

现在的需求为：点击地图中任意一块区域，返回：

1. 若为墙或者主角：无返回值
2. 若为不可通过区域：返回-1
3. 若可以通过，返回最短路径值，并且返回最短路径行走方式（如上两格，返回{2，“WW"}

需求很简单，乍看用各种算法如spfa,a*啥的，但是我们需要在玩家未点击路径前提前算好所有路径（如果点击后再计算就太慢了，影响游戏体验！），而且考虑到后续会加入负边权（陷阱、传送门）以及钥匙、出口等情况（找钥匙后寻找最短出逃路径）。需要借用状态压缩dp的思想去做

先科普一下Dijkstra算法

Dijkstra算法求最短路径

此处摘抄

https://www.cnblogs.com/flyinggod/p/8671053.html

Dijkstra算法是典型最短路算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。Dijkstra算法是很有代表性的最短路算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。Dijkstra一般的表述通常有两种方式，一种用永久和临时标号方式，一种是用OPEN, CLOSE表方式。
大概过程：
创建两个表，OPEN, CLOSE。OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。

1. 访问路网中里起始点最近且没有被检查过的点，把这个点放入OPEN组中等待检查。
2. 从OPEN表中找出距起始点最近的点，找出这个点的所有子节点，把这个点放到CLOSE表中。
3. 遍历考察这个点的子节点。求出这些子节点距起始点的距离值，放子节点到OPEN表中。
4. 重复2，3，步。直到OPEN表为空，或找到目标点。

回到魔塔问题中

为什么介绍Dijkstra，因为魔塔这个问题中，发现Dijkstra或者其他算法做都可以满足需求，但是用在魔塔这个只有小范围的游戏里速度不够理想
可以通过 大神做的寻路算法集
比较一下各个寻路算法的特性

返回这一个问题，我们需要记录每一个可行进路径的解，在确定行进路径后可以立刻取到结果，所以直接用记录地址的BFS去做效率最高，而且code比较简单
。主要用bfs每次通过比较最短路径,并且添加辅助哈希表记录最短路径即可。
这个运算过程可以夹杂在：移动、战斗动画过程中。

//0路 1墙 9主角 5出口
    int map[6][6]{
   
        {
   0,0,1,0,0,0},
        {
   5,1,0,0,1,1},
        {
   1,0,0,1,0,1},
        {
   1,1,0,1,0,1},
        {
   0,1,0,0,9,0},
        {
   0,0,0,1,0,1},
    };
    int nSize = map.size();
    queue<pair<int,int>> myQue;
    pair<int,string> rMap[6][6]{
   {
   },{
   },{
   },{