马尔可夫过程 与 隐马尔科夫模型

为什么是马尔可夫过程？

马尔科夫过程(Markov process)是一类随机过程。

在已知目前状态(现在)的条件下，它未来的演变(将来)不依赖于它以往的演变(过去)。主要研究一个系统的状况及其转移的理论。它是通过对不同状态的初始概率以及状态之间的转移概率的研究，来确定状态的变化趋势，从而达到对预测未来的目的。

概念

实际应用场景

• 液体中的微粒子运动
• 传染病的传染人数
• 车站的候车人数

两个基本特性

1. 无后效性

是指如果在某个阶段上过程的状态已知，则从此阶段以后过程的发展变化仅与此阶段的状态有关，而与过程在此阶段以前的阶段所经历过的状态无关。

我的一句话总结：未来的结果，不看过去，就看现在。

2. 便利性

不管事物出现在什么状态，较长一段时间内，马尔可夫过程逐渐趋于稳定，与初始状态无关。

马尔科夫链Markov chain

马尔科夫链(Markov chain) 是指具有马尔科夫性质的离散事件随机过程，即时间和状态参数都是离散的马尔科夫过程，是最简单的马尔科夫过程。

隐马尔科夫模型（重点）

隐马尔可夫模型(Hidden Markov Model, HMM)作为一种统计分析模型，创立于20世纪70年代。

一句话总结：隐马尔可夫模型，是统计学的，主要做统计分析的。

隐马尔可夫模型(Hidden Markov Model, HMM)是结构最简单的动态贝叶斯网这是一种著名的有向图模型，主要用于时序数据建模(语音识别、自然语言处理等）。

贝叶斯与朴素贝叶斯都是对隐马尔可夫模型做的铺垫。那两个就属于是“抛砖”了！
有向图：有明确的开始和结束，有方向
无向图：没有明确的开始和结束。
任何一个时序序列里面，有开始和结束时间。一定是有向图了！

隐马尔可夫模型是马尔可夫链的一种，它的状态不能直接观察到，但能通过观测向量序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态,每一个观测向量是由一个具有相应概率密度分布的状态序列产生。

马尔可夫链，就是描述一种状态的序列，每一个状态值，取决于前面的有限个状态

隐马尔科夫模型 模型图

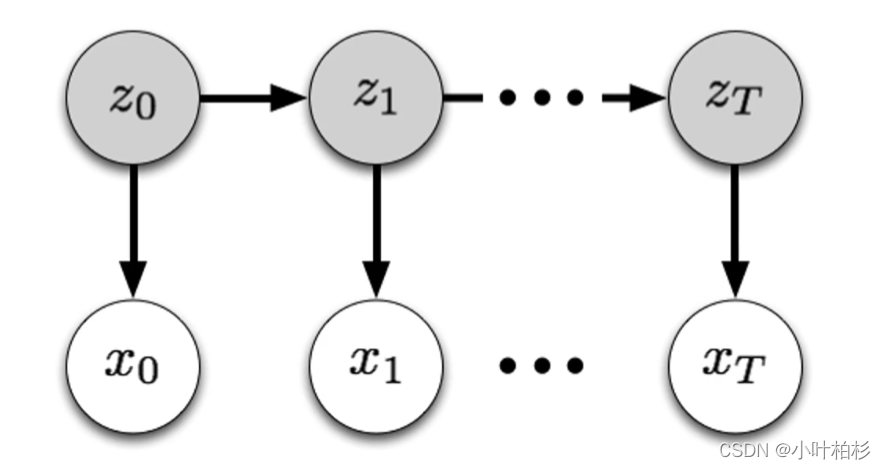
箭头：表示了变量之间的依赖关系，也就是任意一个时刻，观测到变量的取值，仅依赖于该时刻的状态变量。
例如：x1 由 z1来确定的，与其他变量的取值无关。
同时在T时刻，状态 zT 时刻，仅依赖于 T-1 时刻的状态。

说白了这仅是一个链式结构，当前时刻的状态，仅取决于前一个时刻，和其他时刻无关。和过往的，以前的，是没有任何关系的，不依赖的。

隐马尔科夫模型 的构成

隐马尔可夫模型由五个要素组成，其中两个状态集合(N、M)，三个概率矩阵(A、B、π)：

1. N，表示模型中的状态数，状态之间可以相互转移。

上图的 x0,x1,x2……xT

2. M，表示每个状态不同的观察符号，即输出字符的个数。

理解为 输出的个数

3. A，状态转移概率分布。

模型在各个状态之间转换的概率。例如：一个状态“好”，下一时刻状态“好”的概率是多少

4. B，观察符号在各个状态下的概率分布。

输出的观测概率值。模型根据当前状态所得出各个观测值的概率

5. π，表示初始状态分布。

初始时候，模型的各个状态都出现，出现的概率是多少

输入: HMMs的五元组(N, M，A, B, π)。
输出:–个观察符号的序列，这个序列的每个元素都是M中的元素。

输出都是 M，表示每个状态不同的观察符号。
根据概率求出一个输出值，把输出的内容会组成一个集合。输出的集合可以定位出M，每一个符号都是M种类的元素。

应用场景

• 中文分词：一句话中需要填空，“今天早上上语文课，我需要带一本（）书”，A.英语 B.数学 C.语文，通过这个状态，可以一个值一个值的概率预测，找到可能是“语文书”
• 机器翻译
• 语音识别
• 通信中的译码

隐马尔科夫模型 是传统的机器学习模型，并不属于深度学习模型，但深度学习模型很大程度上依赖于机器学习模型。
隐马尔科夫模型 也是非常常用的模型。

用一个小故事理解 隐马尔科夫模型

附：下面转引网络文章《爱情的隐式马尔可夫模型(Love in the Hidden Markov Model)》片断：

首先感谢原英文作者Tom Yeh的精彩描述，生动地讲述了HMM模型的原理，在此我斗胆用我自己的语言用中文修改描述一次。

男生和女生分别是来自不同星球的科学事实已经众所周知的了。男生们总是认为，女生们都是谜一样的生物，他们的情感状态浮动似乎是以秒单位在变化的，难以理解，更勿论预测了! 而女生们觉得男生都是没有感觉动物，完全不能理解什么叫感受-尽管已经告诉他们N次了!这种男女之间的根本差别，导致了他们之间的感情关系是受一种超级无敌复杂的系统所支配的。

不过，我们可以用一个叫隐式马尔可夫(Hidden Markov Model)的数学模型来分析这个系统。

小明，作为一名计算机科学家，决定要系统地去分析他女朋友的情感不确定性，挖掘出里面的规律!于是乎，小明仔细地记录了半年来他女朋友小丽每天的喜怒哀乐变化状态，并作了一张图表来表示小丽的历史情感变化。小明想知道，有了这些数据，他能否从中得出知道，如果小丽某天的情感状态是高兴，那么第二天她更多的是保持好心情呢，还是更多地变得悲伤了，如此等等……

数据胜于雄辩。小明从这半年的数据里面发现，当小丽高兴的时候，3/4的情况下第二天她仍然保持着好心情，只有1/4的情况小丽第二天心情会改变，比如变得气愤，悲伤等等。小明继续分析其他各种情感状态变化情况，比如从高兴到悲伤，悲伤到气愤，高兴到气愤等所有的可能组合。很快小明就得到所有的组合变化数据，从中得知对于任意小丽的某天情感状态下，下一个最有可能的情感状态。

这个过程，同学们，就是有名的 “马尔可夫过程” (Markov process)

不过需要注意的是，马尔可夫过程有一些假设的前提。在我们的例子里面，预测下一天小丽的心情，我们只依赖当天小丽的心情，而没有去考虑更先前她的心情。很明显这种假设下的模型是远不够精确的。很多时候，随着日子一天一天的过去，女生一般会变得越来越体谅。经常女生生气了几天后，气就会慢慢消了. 比方说如果小丽已经生气了3天了，那么她第二天变得高兴起来的可能性，在多数情况下，要比她只生气了一天而第二天变得高兴的可能性要高。马尔可夫过程并没有考虑这个，用行话讲，就是马尔可夫模型忽略远距离历史效应 ( long range dependency)。

有些时候，我们无法直接观测一个事物的状态。比方说，有些女生是很能隐瞒自己的情感而不流露出来的！她们可能天天面带微笑但不代表他们就天天高兴。因此我们必须要有窍门，去依赖某些我们能够直接观察到的东西。

话说回来，我们的主人公小明，自从被小丽发现他这种近乎变态的科学分析行为后，变得非常善于隐藏自己的心情，导致某天小明错误估计了小丽的心情！在误以为那天小丽会心情好的情况下，小明告诉小丽自己不小心摔坏了她心爱的iPod…，小明没想到其实那天小丽正因为前一天错过了商场名牌打折扣的活动而异常气愤。一场血雨腥风过后，两个人最终分手了。

不过，小明凭着自身的英俊高大潇洒，很快又交上了另外一个女朋友，小玲。鉴于小明意识到，女生表面的情感流露非常不可靠，小明决定要另寻他径，继续预测女朋友的心情！(作为一个科学家，小明的确有着不怕碰壁的精神)小明每个月都帮小玲付信用卡的费用(真不明白，有这样的男朋友，小玲有什么理由不高兴啊)，因此小明每天都可以通过Online banking知道小玲每天都买了什么东西。小明突然灵机一动: “没准我能通过观测她的购物规律，推导预测出小玲的心情！”

听起来有点匪夷所思，不过这个过程，的的确确是可以使用叫作隐式马尔可夫的数学模型来表示并分析的。

由于我们需要预测的变量 - 心情状态是无法直接观测的，是隐藏 (Hidden) 起来的，因此这种模型才叫隐式马尔可夫模型。

隐马尔可夫模型在计算机语音识别等领域取得了惊人的成功。据称：“到目前为止，HMM(隐马尔可夫模型)一直被认为是实现快速精确的语音系统的最成功的方法。”