计算二阶矩阵特征值的技巧

1.计算二阶矩阵特征值的技巧

笔记来源：计算二阶矩阵特征值的妙计

1.1 平均特征值

1.2 特征值的积

1.3 求解特征值

根据以上两点，求出特征值

$m$ 为平均特征值 $\frac{{\lambda }_1+{\lambda }_2}{2}$（两个特征值 ${\lambda }_1、{\lambda }_2$ 关于平均特征值中心对称）

$p$ 为两个特征值 ${\lambda }_1、{\lambda }_2$ 的积（$m-d$ 为 ${\lambda }_1$、$m+d$ 为 ${\lambda }_2$）

$-\sqrt{m^2-p}$ 为平均特征值和第一个特征值 ${\lambda }_1$ 间的距离

$+\sqrt{m^2-p}$ 为平均特征值和第二个特征值 ${\lambda }_2$ 间的距离

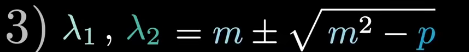
例子：

1.4 泡利矩阵

三个 $x,y,z$ 分方向的旋转

三个 $x,y,z$ 分方向的旋转综合得到一个旋转效果

原先我们需要经过两个步骤才能求解得到特征值

经过本篇的技巧，我们直接跳过求特征多项式这一步，直接由二阶矩阵求得特征值