文章目录
HyCon:用于多模态情感分析的三模态表征混合对比学习
总结:提出了一种用于跨模态表征混合对比学习的新型框架 HyCon ,能够学习模态内模态间的动态,同时探索类间关系。优点:没有引入额外的参数,模型结构简单,降低了过拟合的概率。通过使用三种对比损失来分别实现不同的特征学习。
文章信息
作者:Sijie Mai,Haifeng Hu
单位:中山大学
会议/期刊:IEEE Transactions on Affective Computing(SCI Q2)
题目:Hybrid Contrastive Learning of Tri-Modal Representation for Multimodal Sentiment Analysis
发布日期:2023 年 9 月 13 日
代码:无
数据集:CMU-MOSI、CMU-MOSEI、IEMOCAP
算力要求:GTX 1080 Ti(11G)
研究目的
在多模态情感分析领域,以往的大多数研究都侧重于探索模态内和模态间的交互。然而,由于模态之间的差距,利用跨模态信息(语言、音频和视频)训练网络仍然具有挑战性。此外,虽然每个样本内的动态学习备受关注,但样本间和类间关系的学习却被忽视。(如何学习到多模态数据有意义的表征?)
研究内容
作者提出了一种新型框架 HyCon,用于三模态表征的混合对比学习。具体来说,同时进行模态内、模态间对比学习和半对比学习,这样模型就能充分探索跨模态交互,学习样本间和类间关系,缩小模态差距。此外,还引入了细化项和模态边界,以便更好地学习单模态配对。并且还设计了配对选择机制,以识别信息量大的负配对和正配对,并为其分配权重。
- MSA 的新型学习框架:提出了一种基于对比学习的新型三模态表征学习框架。考虑到现有研究中忽略的样本间和类间关系,HyCon 探索了类间和样本间的关系,以获得更具区分度的联合嵌入。
- 所提出的学习策略:设计了三种损失,即模态内对比学习( IAMCL )、模态间对比学习( IEMCL )和半对比学习( SCL ),以监督和无监督的方式全面地学习模态间/模态内动态。
- 设计了细化项和模态边界,来实现更好的表征学习能力。细化项侧重于正对学习,以更好地对齐来自不同样本的信息。而模态边界可以在对齐模态时保留特定模态的信息。
- 设计了一种配对选择机制,以识别并突出有信息量的正配对和负配对。
研究方法
1.HyCon模型结构
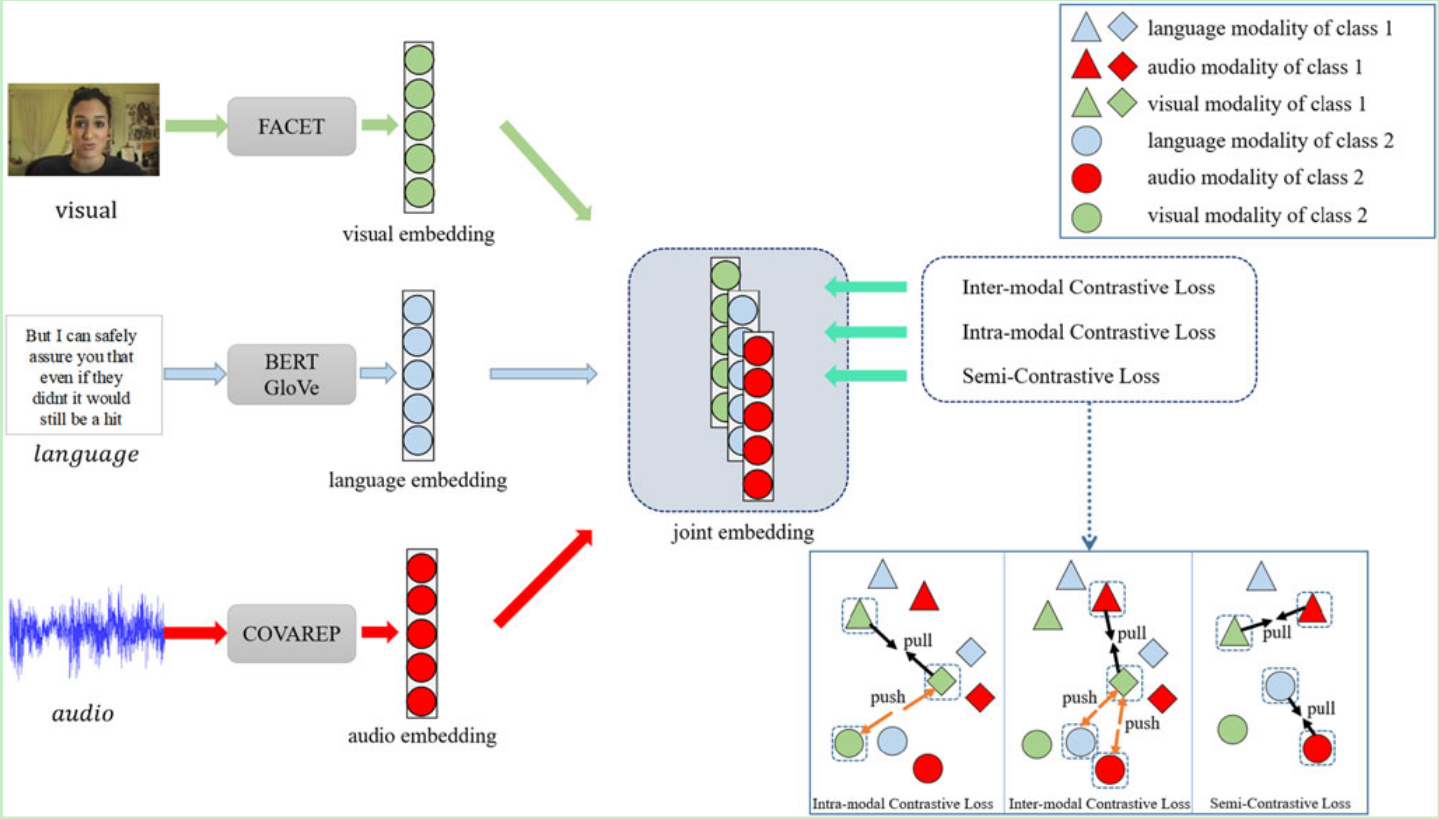
总体流程:给定输入语篇后,首先通过单模态学习网络获得单模态表征。然后,根据不同的对比损失生成正反两方面的单模态表征对。之后,在训练阶段,模型将通过设计的对比学习来学习跨模态交互和类间关系,这些关系将在推理时被舍弃。最后,用简单的融合方法将学习到的单模态嵌入进行融合。HyCon 由以下几个主要部分组成:
- 单模态特征提取网络。用于获取三种模态的单模态潜在空间,利用Transformer提取音频和视觉模态的特征,利用Bert提取语言模态的特征。
X m = F m ( u m ; θ m ) , m ∈ { l , a , v } x m = X T m m ∈ R d × 1 , \begin{aligned}&X^m=F^m(\boldsymbol{u}^m;\theta^m),m\in\{l,a,v\}\\&x^m=X_{T_m}^m\in\mathbb{R}^{d\times1},\end{aligned} Xm=Fm(um;θm),m∈{l,a,v}xm=XTmm∈Rd×1,
| 符号 | 含义 |
|---|---|
| F m F^m Fm | 单模态特征提取网络。 |
| u m u^m um | 输入数据。 |
| x m x^m xm | 映射的单模态表征,是 X m X^m Xm在最后一个时间步中的特征向量。 |
- 配对生成策略。用 K 个样本构建每个迷你批次(每个样本包括音频、视频和语言模态)。在训练阶段,从迷你批次中随机抽取正对和负对,根据不同的损失对模型进行训练。模型可以生成数倍于样本数的配对,从而最大限度地利用数据集,获得更好的泛化能力。
- 混合对比学习。设计了三个版本的对比损失,进行模态内/模态间学习。
- 半对比学习(Semi-Contrastive Learning):半对比学习(SCL)只考虑正对,以学习同一样本的不同模态之间的相互作用,从而最大限度地缩小模态差距。
- 模态内对比学习(Intra-modal Contrastive Learning ):IAMCL 采用监督方式学习不同样本之间的模态内动态,在一个迷你批次中考虑多个正对和负对。
- 模态间对比学习(Inter-modal Contrastive Learning ):IEMCL 也是以有监督的方式学习模态间动态,IAMCL 和 IEMCL 都探索类间关系(样本间关系)。
- 融合机制。Connection简单的相加。
y M = F M ( x l , x a , x v ; θ M ) , ℓ = ∣ y − y M ∣ , y_M=F^M(x^l,x^a,x^v;\theta_M),\ell=|y-y_M|, yM=FM(xl,xa,xv;θM),ℓ=∣y−yM∣,
| 符号 | 含义 |
|---|---|
| F M F^M FM | 多模态融合网络 |
| y y y | 真实标签 |
| y M y_M yM | 预测标签 |
| ℓ \ell ℓ | 平均绝对误差(MAE)或交叉熵损失 |
2.三种对比学习设计
2.1 SCL: Semi-Contrastive Learning(半对比学习)
SCL是无监督的。SCL 的设计目的是学习同一样本中的跨模态动态(模态间动态),从而最大限度地缩小模态差距。它只考虑正对(因此称之为半对比学习),其中正样本被定义为同一样本、不同模态的单模态表征。
对于每个mini-batch中每个模态的表征
a
m
a^m
am,SCL会生成两个正样本
S
=
{
p
1
m
1
,
p
2
m
2
}
S=\{\boldsymbol{p}_1^{m_1},\boldsymbol{p}_2^{m_2}\}
S={p1m1,p2m2} (
m
,
m
1
,
m
2
∈
{
l
,
a
,
v
}
,
m
≠
m
1
,
m
1
≠
m
2
and
m
≠
m
2
m,m_1,m_2\in\{l,a,v\},m\neq m_1,m_1\neq m_2\text{ and }m\neq m_2
m,m1,m2∈{l,a,v},m=m1,m1=m2 and m=m2)。每个pair的打分函数(scoring function)是单模态表征的公共点积。半对比学习的损失如下:
L
S
C
L
=
E
s
[
1
2
∑
i
=
1
2
∥
(
a
m
)
T
p
i
m
i
−
α
∥
2
]
,
m
∈
{
l
,
a
,
v
}
,
\boldsymbol{L}_{SCL}=E_s\left[\frac12\sum_{i=1}^2\left\|(\boldsymbol{a}^m)^T\boldsymbol{p}_i^{m_i}-\boldsymbol{\alpha}\right\|^2\right], m\in\{l,a,v\},
LSCL=Es[21i=1∑2
(am)Tpimi−α
2],m∈{l,a,v},
| 符号 | 含义 |
|---|---|
| E s E_s Es | 在所有可能的集合 S S S上求期望 |
| α \alpha α | 不同模态之间的模态边界,允许存在一定的模态分布差异,以保留用于融合的模态特异性信息。 |
2.2 IAMCL: Intra-Modal Contrastive Learning(模态内对比学习)
IAMCL的设计目的是通过有监督的方式学习模态内动态和类间关系,从而在特征空间中建立更具区分度的边界。在 IAMCL 中,正对被定义为来自同一模态、同一类别的两个不同样本的单模态表征,负对被定义为来自同一模态、不同类别的两个样本的单模态表征。
对于mini-batch(size为K)中每个锚点的每个模态
m
m
m,生成一个由N个positive样本和M个negative样本构成的集合
S
=
{
p
1
m
,
p
2
m
,
…
,
p
N
m
,
n
1
m
,
n
2
m
,
…
,
n
M
m
}
,
m
∈
{
l
,
a
,
v
}
S=\{\boldsymbol{p}_1^m,\boldsymbol{p}_2^m,\ldots,\boldsymbol{p}_N^m,\boldsymbol{n}_1^m,\boldsymbol{n}_2^m,\ldots,\boldsymbol{n}_M^m\},m\in\{l,a,v\}
S={p1m,p2m,…,pNm,n1m,n2m,…,nMm},m∈{l,a,v},其中(
N
+
M
=
K
−
1
N + M = K - 1
N+M=K−1,K是固定的,但是N和M的数量是随机的)。模态内对比学习的损失如下:
L
I
A
M
C
L
=
−
E
s
[
∑
i
=
1
N
(
a
m
)
T
p
i
m
∑
i
=
1
N
(
a
m
)
T
p
i
m
+
∑
j
=
1
M
(
a
m
)
T
n
j
m
]
L_{IAMCL}=-E_s\left[\frac{\sum_{i=1}^N\left(\boldsymbol{a}^m\right)^T\boldsymbol{p}_i^m}{\sum_{i=1}^N\left(\boldsymbol{a}^m\right)^T\boldsymbol{p}_i^m+\sum_{j=1}^M\left(\boldsymbol{a}^m\right)^T\boldsymbol{n}_j^m}\right]
LIAMCL=−Es[∑i=1N(am)Tpim+∑j=1M(am)Tnjm∑i=1N(am)Tpim]
但是该损失很可能会陷入一个次优解,即
a
T
n
j
a^Tn_j
aTnj最小化,但
a
T
p
j
a^Tp_j
aTpj并未最大化。(原因:当负配对的相似度近似为零时,无论正配对的相似度如何,损失值几乎都是最小的。当负对的数量很少时,这种现象会更加严重,
∑
j
=
1
M
(
a
m
)
T
n
j
m
\sum_{j=1}^M\left(\boldsymbol{a}^m\right)^T\boldsymbol{n}_j^m
∑j=1M(am)Tnjm会很容易接近0。)所以,**引入了一个细化项(refinement term)**以确保正对的相似性最大化,具体如下:
L
I
A
M
C
L
R
=
E
s
[
1
N
∑
i
=
1
N
∣
∣
(
a
m
)
T
p
i
m
−
1
∣
∣
2
]
,
m
∈
{
l
,
a
,
v
}
L
I
A
M
C
L
←
L
I
A
M
C
L
+
L
I
A
M
C
L
R
,
\begin{aligned} &L_{IAMCL}^{R} =E_s\bigg[\frac1N\sum_{i=1}^N\bigg|\bigg|(\boldsymbol{a}^m)^T\boldsymbol{p}_i^m-1\bigg|\bigg|^2\bigg], m\in\{l,a,v\} \\ &L_{IAMCL} \leftarrow L_{IAMCL}+L_{IAMCL}^R, \end{aligned}
LIAMCLR=Es[N1i=1∑N
(am)Tpim−1
2],m∈{l,a,v}LIAMCL←LIAMCL+LIAMCLR,
| 符号 | 含义 |
|---|---|
| a m a^m am | 锚点样本表征 |
| p i m p_i^m pim | positive样本表征 |
| n j m n^m_j njm | negative样本表征 |
| L I A M C L R L_{IAMCL}^{R} LIAMCLR | IAMCL的细化损失 |
2.3 IEMCL: Inter-Modal Contrastive Learning(模态间对比学习)
IEMCL 的目的也是学习模态间动态。但是 IEMCL 与 SCL 的不同之处在于,SCL 侧重于学习同一样本中的模态间互动,而 IEMCL 则探索不同样本之间的模态间互动。在 IEMCL 中,正对被定义为来自同一类别、不同样本的两个具有不同模态的单模态表征,而负对则被定义为来自不同类别的两个样本的具有不同模态的单模态表征。
对于大小为K的mini-batch来说,与IAMCL相比,IEMCL的负对和正对数量是IAMCL的两倍。(因为IAMCL针对同一模态,但是IEMCL针对不同模态)模态间对比学习的损失如下:
L
I
E
M
C
L
=
−
E
s
[
∑
i
=
1
2
N
(
a
m
)
T
p
i
∑
i
=
1
2
N
(
a
m
)
T
p
i
+
∑
j
=
1
2
M
(
a
m
)
T
n
j
]
L_{IEMCL}=-E_s\left[\frac{\sum_{i=1}^{2N}\left(\boldsymbol{a}^m\right)^T\boldsymbol{p}_i}{\sum_{i=1}^{2N}\left(\boldsymbol{a}^m\right)^T\boldsymbol{p}_i+\sum_{j=1}^{2M}\left(\boldsymbol{a}^m\right)^T\boldsymbol{n}_j}\right]
LIEMCL=−Es[∑i=12N(am)Tpi+∑j=12M(am)Tnj∑i=12N(am)Tpi]
同样为了防止损失陷入次优解,引入细化项来确保正对的相似性最大化。
L
I
E
M
C
L
R
=
E
s
[
1
2
N
∑
i
=
1
2
N
∥
(
a
m
)
T
p
i
−
α
∥
2
]
,
m
∈
{
l
,
a
,
v
}
L
I
E
M
C
L
←
L
I
E
M
C
L
+
L
I
E
M
C
L
R
,
\begin{aligned}&\boldsymbol{L}_{IEMCL}^R=E_s\left[\frac1{2N}\sum_{i=1}^{2N}\left\|(\boldsymbol{a}^m)^T\boldsymbol{p}_i-\boldsymbol{\alpha}\right\|^2\right], m\in\{l,a,v\}\\&\boldsymbol{L}_{IEMCL}\leftarrow\boldsymbol{L}_{IEMCL}+\boldsymbol{L}_{IEMCL}^R,\end{aligned}
LIEMCLR=Es[2N1i=1∑2N
(am)Tpi−α
2],m∈{l,a,v}LIEMCL←LIEMCL+LIEMCLR,
⚠️:
p
i
,
n
j
p_i,n_j
pi,nj与
a
m
a^m
am模态不同
| 符号 | 含义 |
|---|---|
| L I E M C L R \boldsymbol{L}_{IEMCL}^R LIEMCLR | IEMCL的细化损失 |
3.样本对的构建
采用了一种非参数配对选择机制,动态选择并突出有效的训练对,丢弃无信息的对。
实现:计算每一对的点积,这被称为该对的相似度,然后选择相似度低的正对和相似度高的负对进行训练(困难正样本挖掘和困难负样本挖掘)。对于锚点 a,程序如下所示:
s
p
=
Min
h
(
a
T
p
)
,
s
n
=
Max
h
(
a
T
n
)
,
s^p=\operatorname*{Min}_h(\boldsymbol{a}^T\boldsymbol{p}),\quad s^n=\operatorname*{Max}_h(\boldsymbol{a}^T\boldsymbol{n}),
sp=hMin(aTp),sn=hMax(aTn),
为
L
I
E
M
C
L
L_{IEMCL}
LIEMCL和
L
I
A
M
C
L
L_{IAMCL}
LIAMCL分别选择总共
h
=
K
×
β
h=K\times\beta
h=K×β正负样本对,
β
\beta
β是超参数。然后为选择的样本对根据它们的难度分配权重。
w
i
n
=
e
x
p
(
s
i
n
)
∑
j
=
1
h
e
x
p
(
s
j
n
)
,
w
i
p
=
e
x
p
(
1
s
i
p
+
γ
)
∑
j
=
1
h
e
x
p
(
1
s
j
p
+
γ
)
s
^
i
n
=
s
i
n
⋅
w
i
n
,
s
^
i
p
=
s
i
p
⋅
w
i
p
,
\begin{aligned}&w_i^n=\frac{exp(s_i^n)}{\sum_{j=1}^hexp(s_j^n)},\quad w_i^p=\frac{exp(\frac1{s_i^p+\gamma})}{\sum_{j=1}^hexp(\frac1{s_j^p+\gamma})}\\&\hat{s}_i^n=s_i^n\cdot w_i^n,\quad\hat{s}_i^p=s_i^p\cdot w_i^p,\end{aligned}
win=∑j=1hexp(sjn)exp(sin),wip=∑j=1hexp(sjp+γ1)exp(sip+γ1)s^in=sin⋅win,s^ip=sip⋅wip,
⚠️:应用梯度截断技术来阻止权重
w
i
∗
w_i^*
wi∗的梯度,使其只作为线性标量来辅助训练,而不是可学习的。
| 符号 | 含义 |
|---|---|
| p p p | 锚点a的正样本集合 |
| n n n | 锚点a的负样本集合 |
| s ^ i n , s ^ i p \hat{s}_i^n,\hat{s}_i^p s^in,s^ip | 分别代表负对 i i i和正对 i i i的加权相似度得分 |
| γ \gamma γ | 正标量,确保 s ∗ p + γ s_*^p+\gamma s∗p+γ大于0 |
4.总损失
整体对比损失函数是IAMCL、IEMCL和SCL的加权和:
L
h
y
b
r
i
d
=
λ
1
L
I
A
M
C
L
+
λ
2
L
I
E
M
C
L
+
λ
3
L
S
C
L
,
L_{hybrid}=\lambda_1L_{IAMCL}+\lambda_2L_{IEMCL}+\lambda_3L_{SCL},
Lhybrid=λ1LIAMCL+λ2LIEMCL+λ3LSCL,
整体对比损失与预测损失
ℓ
\ell
ℓ构成总损失:
L
o
v
e
r
a
l
l
=
ℓ
+
L
h
y
b
r
i
d
,
L_{overall}=\ell+L_{hybrid},
Loverall=ℓ+Lhybrid,
实验分析
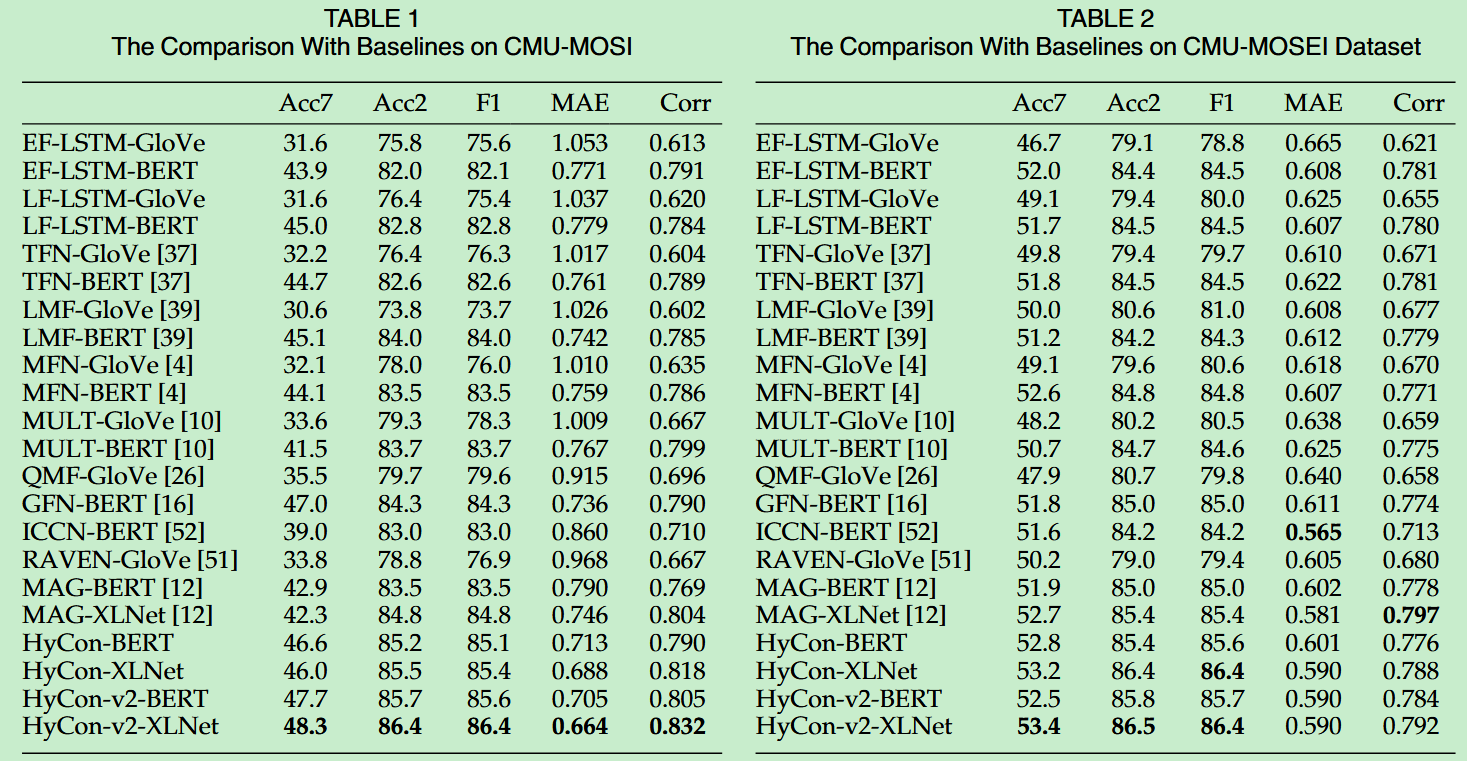
- 通过在CMU-MOSI数据集、CMU-MOSEI数据集上进行了实验,表明了所提出的模型以及配对策略是有效的,并证明了使用更加先进的文本模态编码器对MSA任务是有效的。(Glove、Bert、XLNet均为文本模态编码器,Hycon代表论文所提出的模型,Hycon-v2代表使用了配对策略)
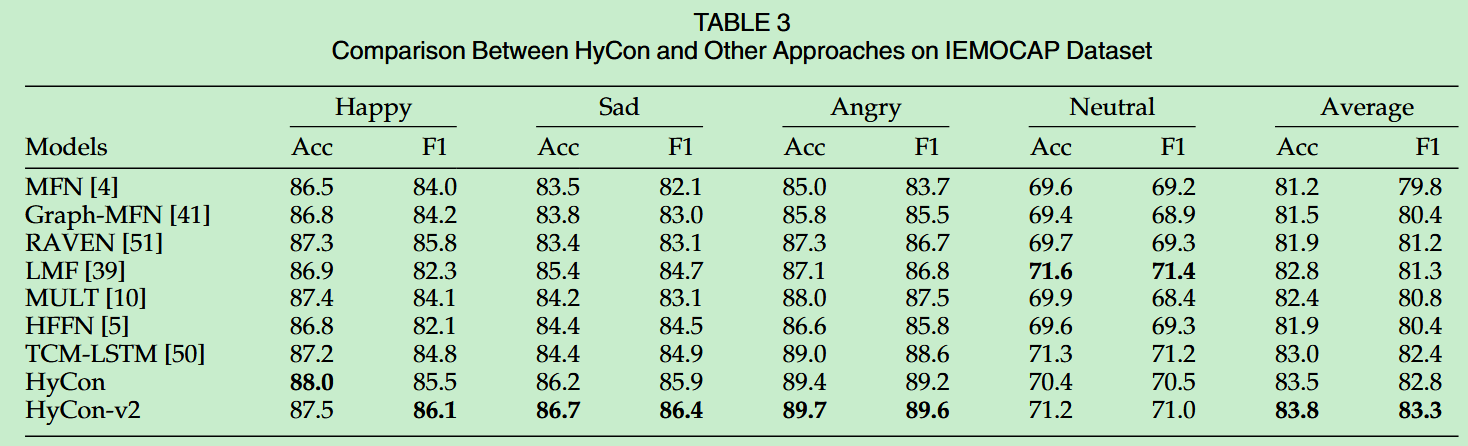
- 为了证明Hycon模型的泛化能力,使用IEMOCAP数据集对模型进行了评估,结果表明模型具有很好的泛化能力。
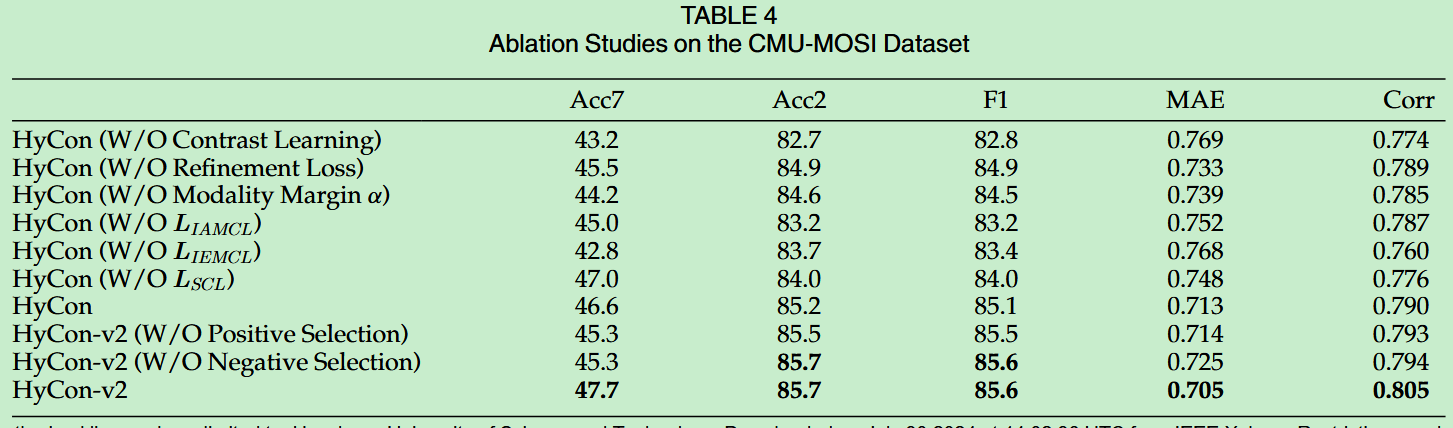
- 通过一系列的消融实验,证明了所设计的对比学习方法的有效性,以及各部分组件和配对机制的有效性。
- 通过探索不同的融合策略,证明了Concatenation的效果最好。这是因为通过使用跨模态对比学习,模态差距可以显著缩小。而且单模态和多模态表征的特征维度被迫具有大致相同的分布,因此直接加法足以探索模态之间的互补信息和交互作用。相反使用复杂的融合方法会引入大量参数,并可能会给特征分布带来噪声,降低MSA任务的性能。
- 通过对模态边界的值进行不同的探索,证明了当 α \alpha α的取值为0.8时,Hycon模型的效果最佳。

- 通过 t-SNE 算法将多模态表征转换为二维特征点并进行可视化,证明了对比学习的有效性。

- 使用传统的对比损失、三元组损失、N-pair损失代替所提出的 L I A M C L , L I E M C L L_{IAMCL},L_{IEMCL} LIAMCL,LIEMCL,证明了在类内和类间样本之间探索跨模态和特定模态动态的想法是有效的。

- 对模型进行了时间与空间复杂性的分析,由于模型融合方式简单,没有引入过多的参数,所以模型的参数量最少。但是训练时间略长,这是因为模型在训练时生成了大量的正负对。

😃😃😃

























 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








