高等数学（数二专题）

---

一、积分的几何应用

1. 求形心坐标

2. 求弧长

下面举出几道例题：

3. 求旋转曲面的面积（侧面积）

圆的表面积公式为 4·π·r² 。

下面举出几道例题：

二、定积分的物理应用

1. 抽水做功—体积

【必记】：dW = ρ · g · 体积 · 移动距离

例题：

2. 变力沿直线做功

【必记】：dW = F · 移动距离

例题：

3. 静水压力—面积

【必记】：dP = ρ · g · h · 受力面积

例题：

4. 万有引力

【必记】：质量 = 线密度 · 长度 ；万有引力 F = G·m₁·m₂ / r²

例题：

三、二阶可降阶方程

1. 二阶可降阶微分方程

2. 伯努利方程（了解）

四、微分方程的物理应用

1. 牛顿第二定律（F = ma）

【必记】：F = m·a ；a = d²x/dt² = dv/dt = v·(dv/dx) ，其中 a = v·(dv/dx) 最常用到。

例题：

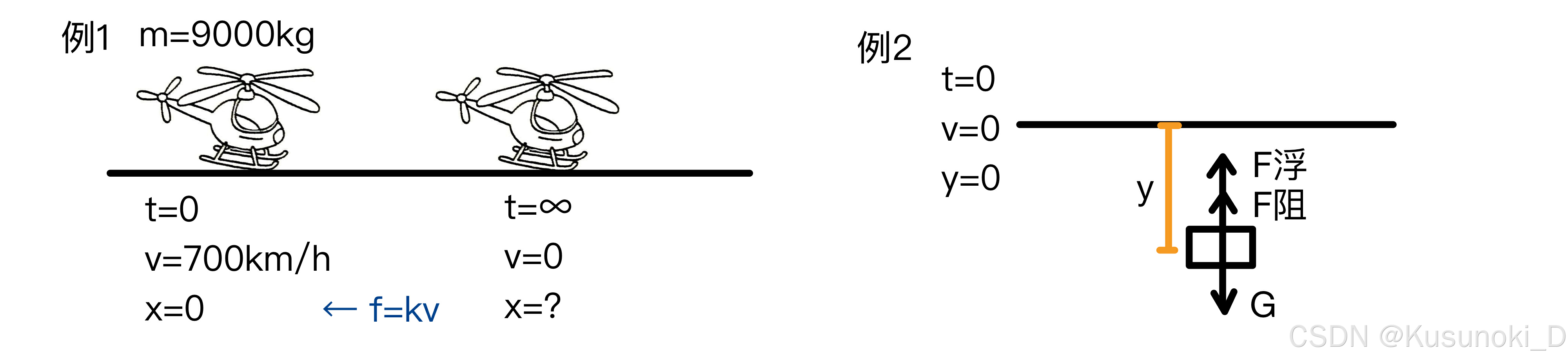
2. 变化率

例题：

3. 进出问题

例题：

时间	湖中A的含量
1999年	5·m0
2000年	m(t)
？年	m0

4. 追击问题

例题：

五、形心质心、曲率圆、相关变化率、已知截面求体积

1. 求形心质心

对于均匀物体（ρ 为一个常数），形心就等于质心。

例题：

2. 曲率与曲率半径、曲率圆

【注】：(x²)^3/2 = √(x²)³ = √(x⁶) = |x| 。

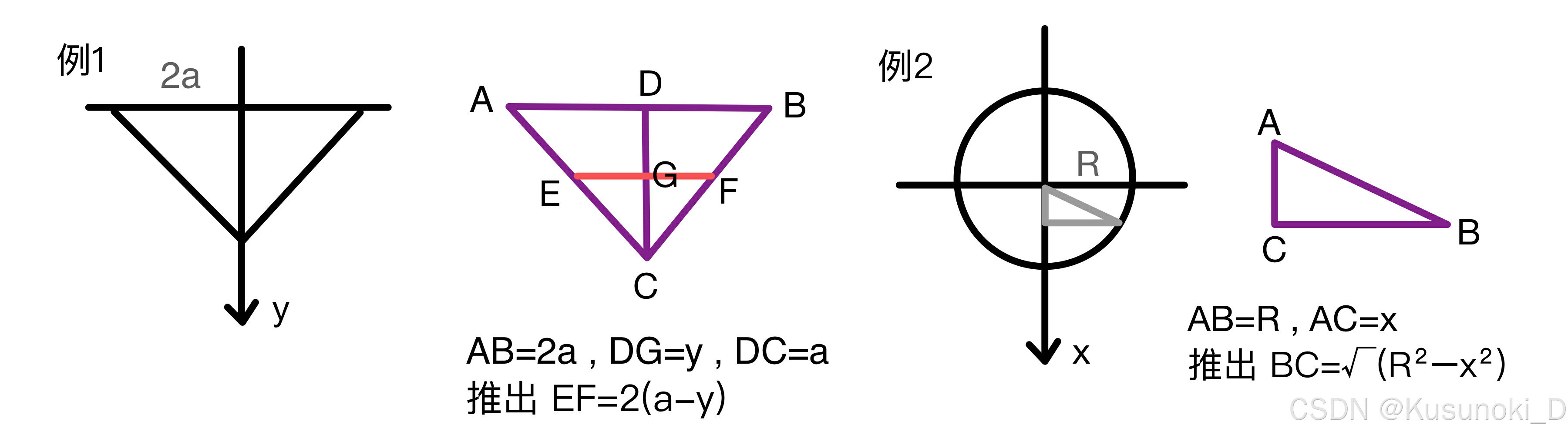
例题：曲线 y² = x 在点 (0,0) 处的曲率圆方程为？
答案：(x-½)² + y² = ¼

3. 平行截面面积为已知的立体的体积

例题：

4. 相关变化率

例题：