机器学习基础认识（一）

一、 机器学习应用

机器学习的应用，主要分为两类：预测、分类

预测，一般是指：根据数据，预测数值
分类，一般是指：根据数据，进行分类

1. 预测与分类的关系【个人理解】

分类，本质上也是一种预测。

预测，可预测实值，也可预测类别。

预测实值可通过线性回归模型，预测出线性的实际数值。
但当预测某个数据的类别（例如男女、老少等非连续的离散值）时，则变为了人们常说的分类问题。

因此，如果非要对预测、分类进行一个严格区分：

『 预测问题是对定量数据的预测，分类问题是对定性数据的预测 』

二、机器学习核心流程

1. 建立模型：根据应用类型，构造函数模型
2. 学习模型：将数据应用于模型计算，并求解出当前模型的最优参数
3. 衡量模型：衡量学习后的模型效果

机器学习的核心流程，就像是做菜-菠萝炒鸡。

👉建立模型，就像是根据目标，凭经验设计一个做菜的固定步骤。

• 开火
• 烧油
• 放菜
• 放盐
• 关火

虽然知道需要什么材料，但这个过程需要多少油，多少盐，多少火力，煮多久——无从知晓！
所以，建立模型时，只知道需要锅碗瓢盆油盐酱醋这些参数，但却不知道参数是多少！！！

👉学习模型，就像是一个鲁莽的菜鸟厨师。
它菜就菜在，不知道这些材料，都需要放多少量（即它也不知道放多少油盐酱醋才好吃）
它莽就莽在，不管三七二十一，先按这个步骤随便放初始量的材料，直接开炒！
每次炒的结果，都由一个试吃小白鼠去尝，如果小白鼠摇摇头不满意，鲁莽的菜鸟厨师就稍微调整一下材料用量

俗话说的好，不怕莽夫莽，就怕莽夫坚持不懈地莽下去。——我人有多俗，这话就有多俗，因为这话就是我这个俗人说的。。。

炒的次数多了，这个材料量自然就会慢慢调整好，小白鼠总有一天会拍灯，为你转身！
于是，鲁莽的菜鸟厨师，经过坚持不懈的尝试与改进，终于含泪掌握了菠萝炒鸡的配方。

其实有点儿“暴力破解法”的思想，就是，我也不知道你什么答案，但我一个个试，总能试出最佳答案！

👉衡量模型，就像是最后的质检，检验你训练后最优状态的模型，是否是个好的模型

• 如果衡量出最优状态模型的效果并不好，说明你当初建模时就有问题了（即，做菜用的材料不对或流程有误等）
• 如果衡量出最优状态模型的效果比较好，说明你当初建的模型，是比较合理的，可以应用！

【学习模型】，只是在尽可能地帮你把当初建立的模型，训练到最优状态；
但这个最优状态下的模型，是否真的实用好用，还是要通过最后一步【衡量模型】来判断的

【比喻还是有些不够恰当的，但精髓到位就行】

1. 建立模型

建立模型，就是根据应用类型，构造函数模型。
应用类型分为：预测、分类。

1.1 预测的函数模型

预测：一般采用线性回归模型。

求解线性回归模型参数，即是学习模型的过程

常见的线性回归函数：一元线性回归【y = wx + b】、多元线性回归【Y=$W^{T}X$】

1.1.1 一元线性回归

一元线性回归【y = wx + b】，只有一个自变量 x，和一个因变量 y，有两个未知参数w和b
它其实就是数学中的一元一次方程。 其中，w是变量x的权重，b是偏差。

一元线性回归，适用于预测只有单个因素影响某个指标的数据，并且该因素与该数据指标，是线性关系才会预测的更准。

例如，假设工资是唯一影响幸福指数的因素，那么可以建立一元线性回归的预测模型。
即：y = wx+b，x表示工资，y表示幸福指数

工资x	幸福指数y
10k	10%
19k	13%
15k	40%
119k	80%
500k	120%
…	…

1.1.2 多元线性回归

多元线性回归【y = $W^{T}X$】，有多个变量x1,x2,x3…xm，构成了自变量X，每一个自变量$x_i$，都有对应的权重w1,w2,w3…wn
即 y = $W^{T}X$ = $w_1\ast x_1+w_2\ast x_2+w_3\ast x_3+....+w_m\ast x_m+w_0\ast x_0$

【这里的$w_0\ast x_0$，其实相当于$x_0=1,w_0=b$，表示偏差b，写成$w_0\ast x_0$，是为了让参数变成一个整齐的向量W
因此，一元线性方程的两个参数w和b，也可以写成多元线性方程：$Y=W^{T}X$】

假设有 m+1个影响因素，则参数w也有m+1个，则多元线性方程为：$W^{T}X$=$\left[\begin{array}{c}{w}_0,w_1,w_2,w_3,...,w_m\end{array}\right]$*$\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\\ ...\\ x_m\end{array}\right]$

这里的$\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\\ ...\\ x_m\end{array}\right]$，表示一条数据
如果有 n 条数据，则应为 X =$\left[\begin{array}{c}{x}_{00},x_{01}...x_{0n}\\ x_{10},x_{11}...x_{1n}\\ x_{20},x_{21}...x_{2n}\\ x_{30},x_{31}...x_{3n}\\ ...\\ x_{m0},x_{m1}...x_{mn}\end{array}\right]$

多元线性回归，适用于由多个因素x影响某个数据指标y的情况。

$Y^T$ = $\left[\begin{array}{c}\overline{y_0},\overline{y_1},\overline{y_2},\overline{y_3},...,\overline{y_n}\end{array}\right]$=$W^{T}X$=$\left[\begin{array}{c}{w}_0,w_1,w_2,w_3,...,w_m\end{array}\right]$$\left[\begin{array}{c}{x}_{00},x_{01}...x_{0n}\\ x_{10},x_{11}...x_{1n}\\ x_{20},x_{21}...x_{2n}\\ x_{30},x_{31}...x_{3n}\\ ...\\ x_{m0},x_{m1}...x_{mn}\end{array}\right]$
或$Y$ = $\left[\begin{array}{c}\overline{y_0}\\ \overline{y_1}\\ \overline{y_2}\\ \overline{y_3}\\ ...\\ \overline{y_n}\end{array}\right]$=$X^{T}W$=${\left[\begin{array}{c}{x}_{00},x_{01}...x_{0n}\\ x_{10},x_{11}...x_{1n}\\ x_{20},x_{21}...x_{2n}\\ x_{30},x_{31}...x_{3n}\\ ...\\ x_{m0},x_{m1}...x_{mn}\end{array}\right]}^T$*$\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ w_3\\ ...\\ w_m\end{array}\right]$

例如，假设颜值和工作，是影响幸福指数的两个因素，那么加上偏差b，总共有3个影响因素x0,x1,x2即如下

1.2 分类的函数模型

分类：一般采用逻辑回归模型（即，线性回归函数+非线性函数）。

逻辑回归模型：线性回归函数+非线性函数
1）先用线性回归函数，计算出一个实值。（例如，线性回归模型-计算出资产为100w）
2）再用非线性函数，对实值按条件进行分类。（例如，根据线性回归模型计算出的资产100w，则分类为“高价值人群”）

这里的非线性函数，其实是激活函数，常见的激活函数有逻辑回归

具体的激活函数有多种，常见的有sigmoid函数（也叫逻辑回归函数）、Relu函数、softmax函数等。

（sigmoid与softmax实际相通，解释不同）

1.2.1 二分类的逻辑回归

二分类的逻辑回归，其实指的就是 sigmoid 函数，又称“对数几率函数”。

二分类，是指只有两种类别，而分类结果是这两种类别中的其中一种。

例如人的性别，只有男、女中的一种；婚育状况，只有已婚、未婚中的一种；生命状态，只有生、死中的一种。

当我们要实现的是二分类问题时，可以选用sigmoid函数。

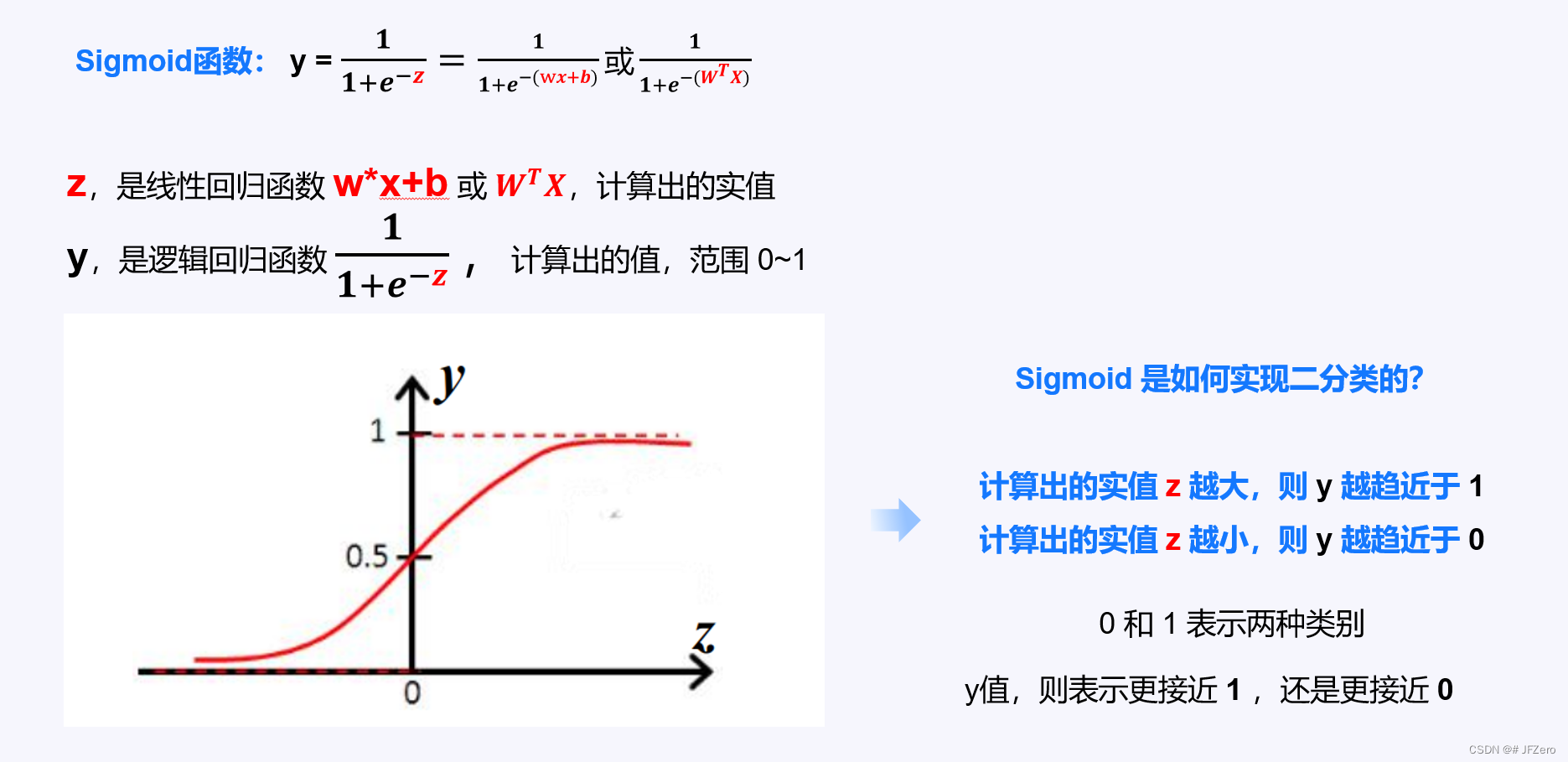
从sigmoid函数可以看出，分类结果是从 y 值来判断的：例如如果以0.5作为分类标准
y>0.5 : 判定类别为 1 （可以自己设置标签，例如，1表示男）
y≤0.5：判定类别为 0（可以自己设置标签，例如，0表示女）

从sigmoid函数，我们能看出未知参数，依然是 W（多元线性方程，以后均用多元线性方程代替一元线性方程）。

总结二分类逻辑回归的计算步骤：先计算多元线性方程 → 再计算逻辑回归方程

多元线性方程：Z = $\left[\begin{array}{c}\overline{z_0}\\ \overline{z_1}\\ \overline{z_2}\\ \overline{z_3}\\ ...\\ \overline{z_n}\end{array}\right]$=$X^{T}W$=${\left[\begin{array}{c}{x}_{00},x_{01}...x_{0n}\\ x_{10},x_{11}...x_{1n}\\ x_{20},x_{21}...x_{2n}\\ x_{30},x_{31}...x_{3n}\\ ...\\ x_{m0},x_{m1}...x_{mn}\end{array}\right]}^T$$\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ w_3\\ ...\\ w_m\end{array}\right]$

二分类逻辑回归方程：Y = $\left[\begin{array}{c}\overline{y_0}\\ \overline{y_1}\\ \overline{y_2}\\ \overline{y_3}\\ ...\\ \overline{y_n}\end{array}\right]$= Sigmoid(Z) =$\left[\begin{array}{c}\frac{1}{1+e^{-\overline{z_0}}}\\ \frac{1}{1+e^{-\overline{z_1}}}\\ \frac{1}{1+e^{-\overline{z_2}}}\\ \frac{1}{1+e^{-\overline{z_3}}}\\ ...\\ \frac{1}{1+e^{-\overline{z_n}}}\end{array}\right]$

1.2.2 多分类的逻辑回归

多分类的逻辑回归，其实指的就是 softmax 函数，它是sigmoid函数的进化，本质上与sigmoid无差。

多分类，是指有多种类别，而分类结果是这多种类别中的其中一种。【暂不讲其他多分类情况】
例如：声音分为男高音、男中音、男低音、女高音、女低音、女中音这6种类别，分类时只判断为其中一种，则为多分类问题，适用softmax函数。
【举个简单的🌰】

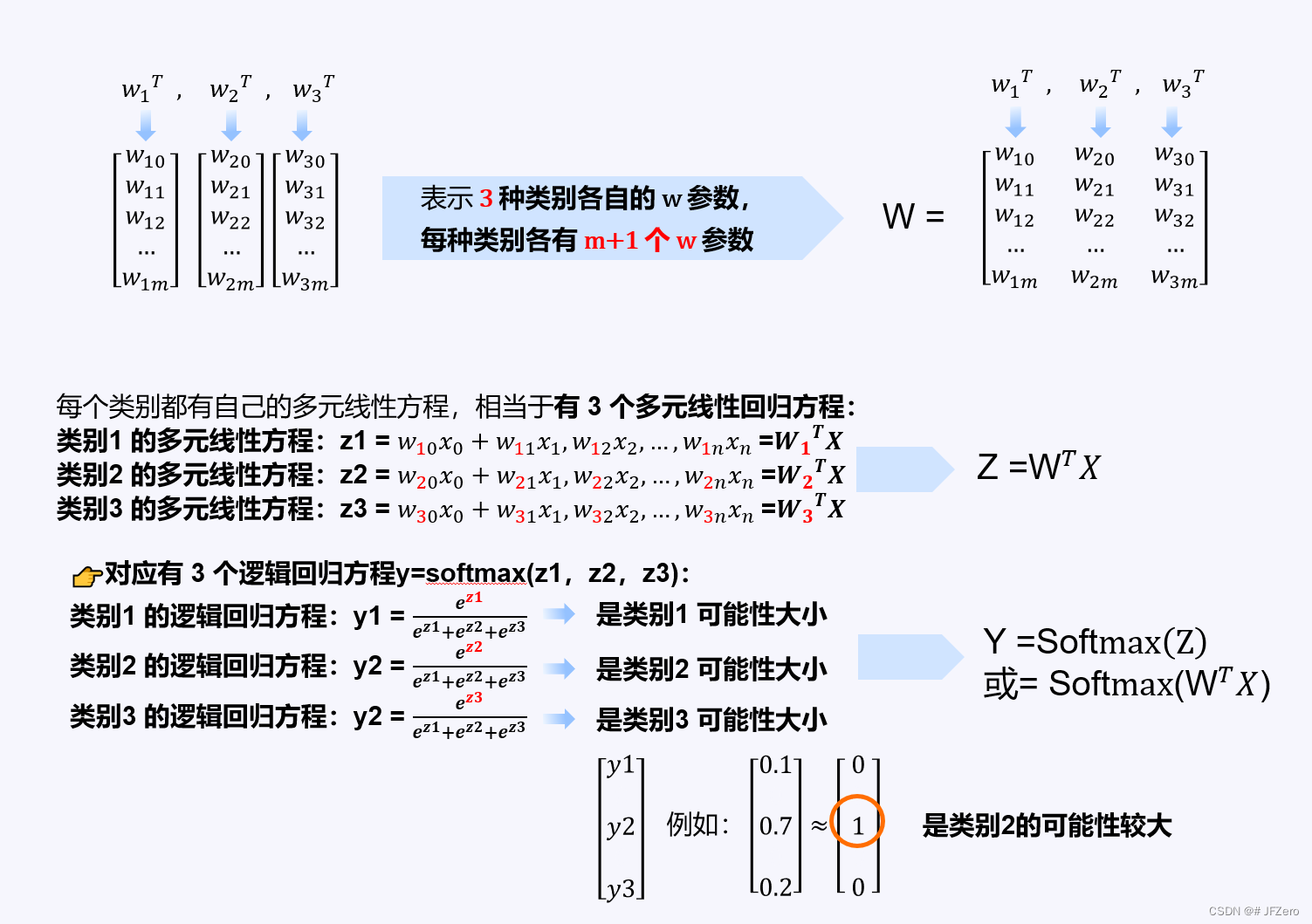
由此可见：
二分类的sigmoid逻辑回归模型，只输出 1 个y值，用于判断是否为某个类别
多分类的softmax逻辑回归模型，则输出多个y值，用于判断多个类别中，可能性最大的那种类别。

为什么说sigmoid函数和softmax函数，本质是一样的呢？

sigmoid函数 y = $\frac{1}{1+e^{-z}}=\frac{e^z}{e^z+e^0}$，相当于判断是否为某个类别：
是该类别，例如性别是男的， $Z1=W{1}^{T}X$；
不是该类别，例如性别不是男的 Z2 = 0*X=0 【二分类问题：不是男的，默认为女】
于是，就可以变形为 $sigmoid函数y=\frac{1}{1+e^{-z}}\to softmax函数y=\frac{e^z}{e^z+e^0}$

妙哉妙哉…

举个简单的sofgmax适用栗子🌰：假设颜值、工资等m个因素，决定了生活的多种价值类型（高、中、低价值）

这样的分类方式，非常肤浅，价值导向问题很大…但简单易懂…

假设生活的价值类型，由m+1个因素决定，于是参数w就有m+1个：w0,w1,w2,…wm。
生活价值有 3 个类型，低价值、中价值、高价值，那么各自的参数为W0,W1,W2
W0 = $\left[\begin{array}{c}{w}_{00}\\ w_{01}\\ w_{02}\\ w_{03}\\ ...\\ w_{0m}\end{array}\right]$, W1 = $\left[\begin{array}{c}{w}_{10}\\ w_{11}\\ w_{12}\\ w_{13}\\ ...\\ w_{1m}\end{array}\right]$, W2 = $\left[\begin{array}{c}{w}_{20}\\ w_{21}\\ w_{22}\\ w_{23}\\ ...\\ w_{2m}\end{array}\right]$
合在一起的 W = [ W0,W1,W2]=$\left[\begin{array}{c}{w}_{00},w_{01},w_{02}\\ w_{01},w_{11},w_{21}\\ w_{02},w_{12},w_{22}\\ w_{03},w_{13},w_{23}\\ ...\\ w_{0m},w_{1m},w_{2m}\end{array}\right]$
👉先建立3个多元线性回归方程，从0开始作为类别序号【0，1，2】
$Z0=W{0}^{T}X或X^T{W}_0$；
$Z1=W{1}^{T}X或X^T{W}_1$；
$Z2=W{2}^{T}X或X^T{W}_2$；

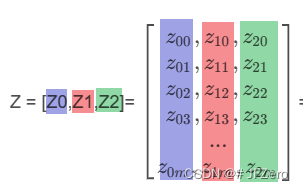
这三个多元线性方程，可以合并为 1 个：

Z = [Z0,Z1,Z2]= $\left[\begin{array}{c}{z}_{00},z_{10},z_{20}\\ z_{01},z_{11},z_{21}\\ z_{02},z_{12},z_{22}\\ z_{03},z_{13},z_{23}\\ ...\\ z_{0m},z_{1m},z_{2m}\end{array}\right]$=$X^{T}W$=${\left[\begin{array}{c}{x}_{00},x_{01}...x_{0n}\\ x_{10},x_{11}...x_{1n}\\ x_{20},x_{21}...x_{2n}\\ x_{30},x_{31}...x_{3n}\\ ...\\ x_{m0},x_{m1}...x_{mn}\end{array}\right]}^T$$\left[\begin{array}{c}{w}_{00},w_{01},w_{02}\\ w_{01},w_{11},w_{21}\\ w_{02},w_{12},w_{22}\\ w_{03},w_{13},w_{23}\\ ...\\ w_{0m},w_{1m},w_{2m}\end{array}\right]$

其中，z0,z1,z2的对应关系如下：

👉再建立多分类逻辑回归模型：
Y = [ Y0,Y1,Y2]=$\left[\begin{array}{c}{y}_{00},y_{10},y_{20}\\ y_{01},y_{11},y_{21}\\ y_{02},y_{12},y_{22}\\ y_{03},y_{13},y_{23}\\ ...\\ y_{0m},y_{1m},y_{2m}\end{array}\right]$=Softmax(Z)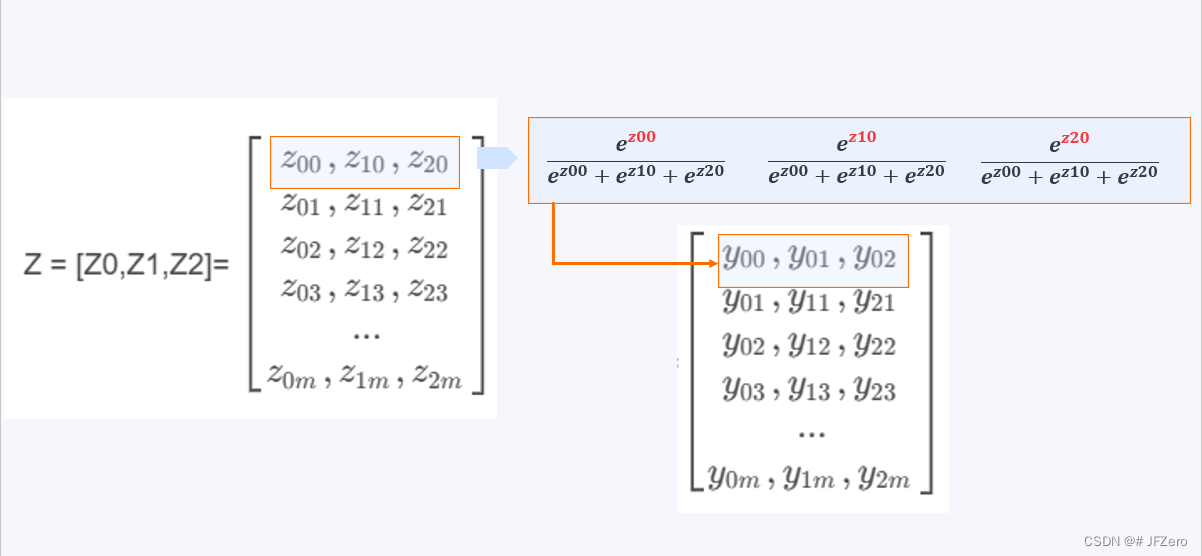

例如
$\left[\begin{array}{c}y1,y2,y3\end{array}\right]=\left[\begin{array}{c}0.2,0.7,0.1\end{array}\right]$≈$\left[\begin{array}{c}0,1,0\end{array}\right]$
判断为第2种类别。

这是一种独热编码one-hot的体现，只有一个值为1，其余值为0。 例如：010和100和001，分别是3种类别

更详细的极大似然估计：极大似然估计法的公式推导-二分类、多分类，损失函数的优化方法

1.3 预测和分类的模型总结

如果要求实现预测，需建立线性回归模型。
👉一元或多元回归模型：$Y=W^{T}X$

参数w的个数，是由影响因素的个数决定的，如果y值由m个x因素影响，则参数w的个数为m，但考虑到偏差b也用$w_0{x}_0$表示
则，

• 参数w为 m+1 个：$W=\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_m\end{array}\right]$;
• 因素x分别为：X = $\left[\begin{array}{c}{x}_{00},x_{01}...x_{0n}\\ x_{10},x_{11}...x_{1n}\\ x_{20},x_{21}...x_{2n}\\ x_{30},x_{31}...x_{3n}\\ ...\\ x_{m0},x_{m1}...x_{mn}\end{array}\right]$,表示 m+1 个因素组成一条数据，共有 n+1 条数据;
• 实值y分别为：根据模型计算出的$\bar{Y}=\left[\begin{array}{c}\overline{y_0}\\ \overline{y_1}\\ \overline{y_2}\\ \overline{y_3}\\ ...\\ \overline{y_n}\end{array}\right]$，实际数据里的$Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\\ ...\\ y_n\end{array}\right]$

如果要求实现分类，需建立逻辑回归模型。
👉二分类逻辑回归模型：
二分类，实际是只有一个类别，因此：
① 先建立一个多元线性回归模型：$Z=W^{T}X$

其中，$W=\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_m\end{array}\right]$

② 再建立一个二分类逻辑回归模型sigmoid：$Y=Sigmoid(Z)=\frac{1}{1+e^{-Z}}$

👉多分类逻辑回归模型：
多分类，实际是有多个类别，例如 3 个，因此：
① 先建立一个多元线性回归模型：$Z=W^{T}X$

其中，W = [ W0,W1,W2]=$\left[\begin{array}{c}{w}_{00},w_{01},w_{02}\\ w_{01},w_{11},w_{21}\\ w_{02},w_{12},w_{22}\\ w_{03},w_{13},w_{23}\\ ...\\ w_{0m},w_{1m},w_{2m}\end{array}\right]$
② 再建立一个多分类逻辑回归模型softmax：$Y=softmax(Z)=\frac{1}{1+e^{-Z}}$

$\left[\begin{array}{c}y1\\ \\ y2\\ \\ y3\end{array}\right]=\left[\begin{array}{c}\frac{e^{W{1}^{T}X}}{e^{W{1}^{T}X}+e^{W{2}^{T}X}+e^{W{3}^{T}X}}\\ \\ \frac{e^{W{2}^{T}X}}{e^{W{1}^{T}X}+e^{W{2}^{T}X}+e^{W{3}^{T}X}}\\ \\ \frac{e^{W{3}^{T}X}}{e^{W{1}^{T}X}+e^{W{2}^{T}X}+e^{W{3}^{T}X}}\end{array}\right]$

注意：模型参数 W未知！

下一步学习模型，目的就是根据已有的 X 和 Y 数据，求解出最优模型的参数 $W_{优}$

2. 学习模型：求解最优模型

学习模型，是根据上一步建立的模型，进行批量数据的计算，求解模型的最优状态。

我们需要思考两个核心问题：

• 什么是模型的最优状态？
• 用什么指标衡量模型状态？
• 如何来达到最优状态？

所以，在学习模型主要分为 3 个步骤：

1）了解什么是模型最优状态
2）明确衡量模型状态的指标
3）明确计算指标最优的方式

先来解决第一个问题：什么是模型的最优状态？

2.1 了解什么是模型最优状态

模型状态如何，是通过判断【当前模型计算结果】与【实际结果】拟合程度，拟合程度可通过损失函数来计算。

在训练模型时，主要是通过【实际结果($y_i$)】对比【根据模型计算出的结果（$\overline{y_i}$)】，来判断模型的计算结果，是否符合实际结果。

$\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ ...\\ y_n\end{array}\right]$ 对比 $\left[\begin{array}{c}\overline{y_0}\\ \overline{y_1}\\ \overline{y_2}\\ ...\\ \overline{y_n}\end{array}\right]$

如果每一个计算结果，都等于（或近似等于）实际结果，这个模型状态无疑是最优的！（先不管过拟合问题）

$y_0=\overline{y_0}$
$y_1=\overline{y_1}$
…
$y_n=\overline{y_n}$

可惜，天不如人意…能尽可能让大部分（相等或相似）拟合就好。

再来解决第二个问题：用什么指标衡量模型的状态？

2.2 明确衡量模型状态的指标

预测的线性回归模型，常用衡量指标为：最小二乘法 - 残差平方和
分类的逻辑回归模型，常用衡量指标为：极大似然估计法 - 似然值

最常用的两个指标：①线性回归模型：残差平方和 ②逻辑回归模型：似然值

2.2.1 线性回归模型：最小二乘法-残差平方和

残差平方和：最小二乘法

残差平方和：通常指两组数据一一对应的残差平方和。

SSE = $\sum ({\bar{y}}_{i计算}-y_{i实际}{)}^2$

当 SST 值最小，则表示模型计算结果，与实际结果差异最小——模型最优！

这种以残差平方和最小为模型最优状态的方法，通常叫“最小二乘法”。

最小二乘法：适用于预测问题，即适用于求解线性回归模型的最优状态。

损失函数，就相当于试吃的小白鼠，用来判断菜味道是否达到最好！

2.2.2 逻辑回归模型：极大似然估计法-似然值

——极大似然估计法即交叉熵法，解释角度不同，但公式相同

似然值：$Y_{实际}$在当前模型下发生的可能性大小，叫做似然值。

当似然值越大，表示$Y_{实际}$在该模型下，发生的概率值较大，即当前模型与实际模型更接近。

极大似然估计法，就是在挑出似然值越大的那个模型。

L = ${\sum }_{}^{}\overline{y_i}.ln{y}_i+(1-\overline{y_i}).ln{y}_i$

似然值（或称交叉熵）越大，模型越优。

极大似然估计法：适用于分类问题，即适用于求解逻辑回归模型的最优状态。

最后来解决第一个问题：如何达到模型的最优状态？

• 如果是最小二乘法，残差平方和最小，则模型最优
• 如果是极大似然估计法，似然值最大，则模型最优

那么如何使最小二乘法的残差平方和最小，如何使极大似然估计法的似然值达到最大呢？

2.3 明确计算指标最优的方式

模型与实际模型的拟合程度指标，可通过损失函数Loss计算可得。

1）最小二乘法：SSE = $\sum ({\bar{y}}_{i计算}-y_{i实际}{)}^2$，求出Loss最小值（即残差平方和Sum of squares for total最小）
2）极大似然估计法：L = ${\sum }_{}^{}\overline{y_i}.ln{y}_i+(1-\overline{y_i}).ln{y}_i$，求出L最大值（即似然值Likelyhood最大）

这两个函数，都可以统一为损失函数 Loss。

最小二乘法的损失函数：Loss = SSE = $\sum ({\bar{y}}_{i计算}-y_{i实际}{)}^2$
极大似然估计法的损失函数：Loss = - L = - ${\sum }_{}^{}[\overline{y_i}.ln{y}_i+(1-\overline{y_i}).ln{y}_i]$

Loss函数，则表示模型计算结果与实际结果的误差，通常称为损失函数。

损失函数值Loss越小，表示模型计算结果与实际结果误差越小，模型越优。

【👉注：在原极大似然估计法L函数前，加负号】
这样，无论是最小二乘法，还是极大似然估计法，它们的损失函数值Loss越小，表示模型计算结果与实际结果误差越小，模型越优。

当 Loss 达到最小值时，说明模型达到最优状态，这时可以明确最优模型的参数 $W_{优}$ 了。

而损失函数求极值，通常有以下两种方法：

• 通过求导，求出解析解，得到精确模型——数学计算求极值
• 通过迭代，求出近似解，逼近较优模型——梯度下降法、牛顿法…

2.3.1 求导：解析解

Loss 函数对参数W求导，并使导数$Los{s}^{{}^{\prime }}$为0，计算出精确的参数 W，使得Loss得到最大值或最小值。

2.3.1.1 最小二乘法-求导解析解

最小二乘法的Loss函数，本质上就是个二元方程，求解二元方程的最小值，直接求导即可。
Loss = $\sum ({\bar{y}}_{i计算}-y_{i实际}{)}^2$

求导数$Los{s}^{{}^{\prime }}=\frac{dLoss(W)}{d(W)}=0时，求解出的W值为模型最优状态下的参数，此时的SSE达到最小值。$

• 对 W 求导，实际是对每一个w0,w1,w2…求偏导$\frac{\partial Loss(w0)}{\partial (w0)}=\frac{\partial Loss(w1)}{\partial (w1)}=\frac{\partial Loss(wi)}{\partial (wi)}=0$
• 最终求得每一个$w_i$，构成最终的$W_{优}$
  

目前sklearn求解多元线性回归模型时，用的是最小二乘法的求导-解析解方式。

最小二乘法-求导公式推导

2.3.1.1 极大似然估计法-求导解析解

极大似然估计法，本质上就是个对数方程，求解它的最大值，直接求导即可。
Loss = ${\sum }_{}^{}\overline{y_i}.ln{y}_i+(1-\overline{y_i}).ln{y}_i$

求导数$L^{{}^{\prime }}=\frac{dLoss(W)}{d(W)}=0时，求解出的W值为模型最优状态下的参数，此时的L达到最大值。$

• 对 W 求导，实际是对每一个w0,w1,w2…求偏导$\frac{\partial Loss(w0)}{\partial (w0)}=\frac{\partial Loss(w1)}{\partial (w1)}=\frac{\partial Loss(wi)}{\partial (wi)}=0$
• 最终求得每一个$w_i$，构成最终的$W_{优}$

解析法难以应对大批量的数据集计算，因此实际常用求近似解，逼近较优模型的方式。

2.3.2 迭代：近似解

迭代法：通过不断地更新模型参数W，求出近似最优的模型。

迭代求解的过程如下：
→ 从W的初始值开始，不断地迭代参数W，使每次迭代的损失函数Loss逐渐变小
→直到Loss达到极小值，即可停止迭代 W，得到模型最优状态下的$W_{优}$ 。

因此，在进行迭代前，需要明确3个问题：
1）W的初始值是多少？
2）如何迭代 W，才能使Loss变小？
3）什么时候停止迭代？

先来解决第一个问题：W的初始值是多少？

2.3.2.1 明确参数初始值

无论是线性回归模型，还是逻辑回归模型，未知参数均为W。

要为 W 设置一个初始值，$W_0$例如
$W^0$ = $\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_n\end{array}\right]$ = $\left[\begin{array}{c}0\\ 0\\ 0\\ ...\\ 0\end{array}\right]$ 或

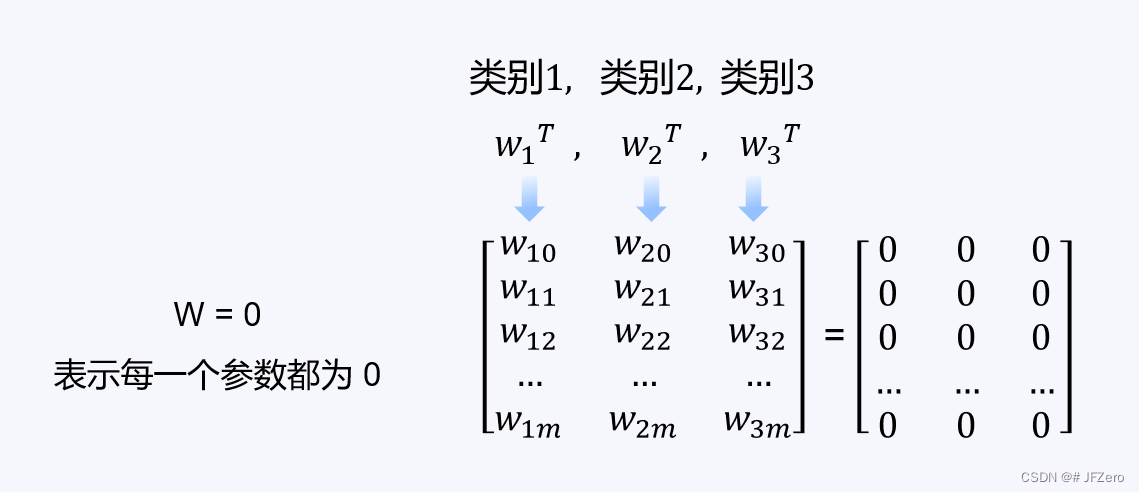
当然，W初始值不一定是0，也可以设置为别的值。

根据初始参数 $W^0=0$，先计算出初始状态模型的$\overline{Y^0}$值
再根据实际$Y$值和模型计算的初始$\overline{Y^0}$值，计算出初始的Loss值，即$Los{s}_0$
最小二乘法：Loss = $\sum ({\bar{y}}_{i计算}-y_{i实际}{)}^2$
极大似然估计法：Loss = -${\sum }_{}^{}(\overline{y_i}.ln{y}_i+(1-\overline{y_i}).ln{y}_i)$

逻辑回归函数及损失函数公式堆导

再来解决第一个问题：如何迭代 W，才能使Loss变小？

2.3.2.2 明确参数迭代方法

迭代参数W的方式有坐标下降法、梯度下降法、牛顿法、拟牛顿法等

a. 梯度下降法

每次迭代的步长 Δ ，为学习率*导数：

$\Delta =\eta \ast \frac{d(Los{s}_k)}{dw}$

$w_{k+1}=w_k-\Delta$

因此，梯度下降法的参数迭代公式为：$w_{k+1}=w_k-\eta \ast \frac{d(Los{s}_k)}{dw}$

1）当前$w_k$下的导数越大，则下次迭代的步长越大。
2）当前$w_k$下的导数越小，则下次迭代的步长越小。

• 这样的迭代方式，可根据函数倾斜程度，自动调整步长。

b. 牛顿法

下次迭代的$w_{k+1}$，为$w_k$处切线方程 ax+b = 0 时的根，步长Δ计算如下图

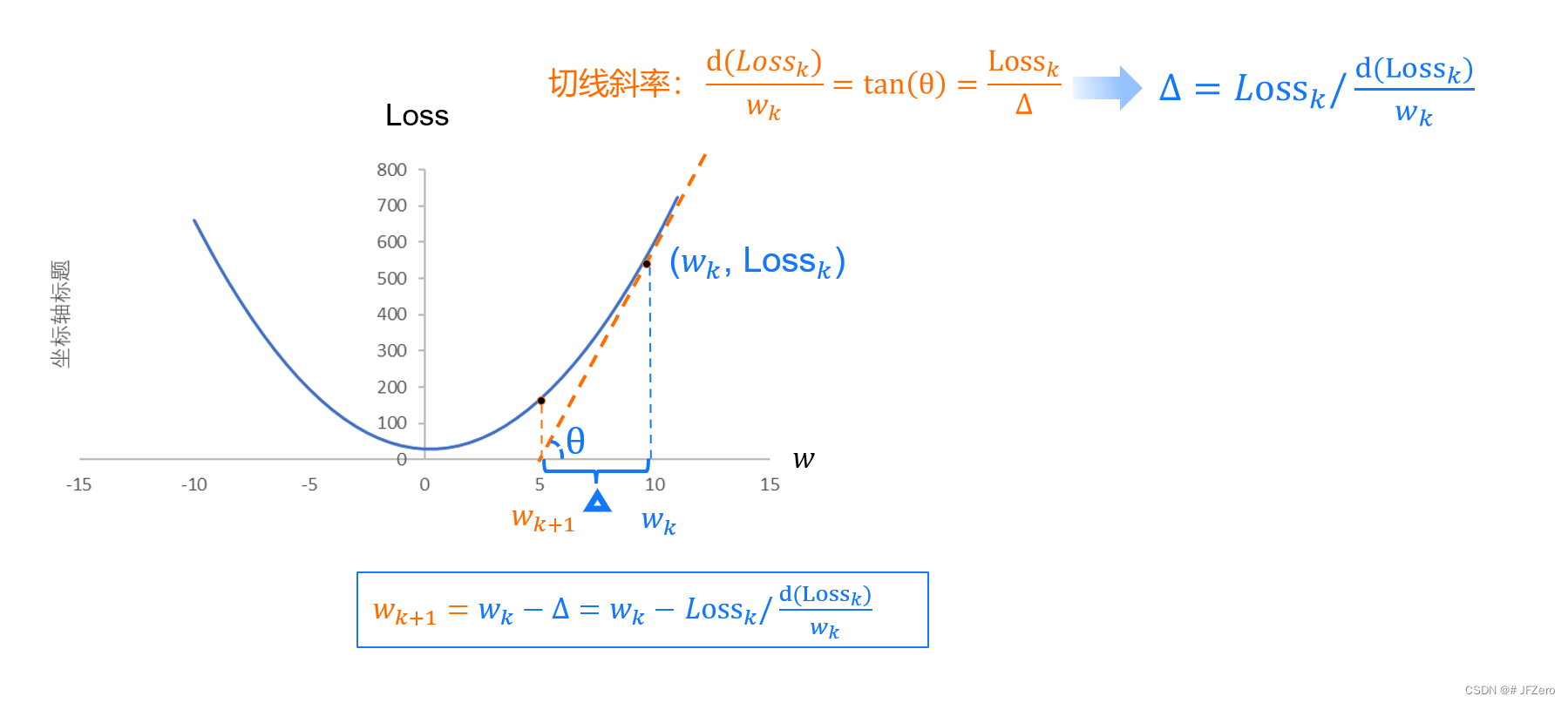
$w_{k+1}=w_k-\Delta$

最终得出迭代公式:$w_{k+1}=w_k-\frac{Los{s}_k}{\frac{d(Los{s}_k)}{dw}}$

c. 拟牛顿法【暂缺】

d. 坐标下降法【暂缺】

与梯度下降法很像，就是通过对每个维度的向量求导

使用梯度下降法或牛顿法，对参数W进行迭代，每次迭代，都可以计算出对应的 Loss 损失函数值。

最后解决第三个问题：什么时候停止迭代？

2.3.2.3 明确停止迭代方式

停止迭代的方式有两种：

①设置损失函数的阈值，当损失函数Loss小于某阈值，即停止迭代

②设置迭代的次数，当迭代次数超过时，即停止迭代（迭代会收敛，迭代次数越多，则越逼近极值）

多次迭代过程中，不断更新模型参数，使模型在迭代过程中逐渐变优。

迭代法的核心是，每次如何更新参数 W？

3. 衡量模型

衡量模型，其实应该用损失函数来衡量模型效果，但损失函数的衡量，缺少参照对比。

例如，如果线性回归模型：最小二乘法的损失函数Loss，计算出的Loss极小值为50，只能说明这个模型当前达到了最优状态。

但并不能说明模型最优状态下的预测或分类效果是好的。

这就好像是，矮子里边拔高个儿，或者是，一群小矮人里的最高个儿，实际也并不高…上限太低

所以，我们需要用别的方式，最好是能够对比衡量拟合程度的指标，来衡量最优状态下的模型效果。

就好比，如果我们说本月销售额达300万，这个销售额到底是好，还是不好呢？——不好说
但如果我们说，本月销售额同比增长 30%，或是本月销售额占年度销售额的90%，这就能说明销售额情况表现比较好！
模型的衡量亦是如此，指标要有对比！

线性回归模型和逻辑回归模型的衡量方式，均有所不同。

3.1 线性回归模型：R²

R²(R squared, Coefficient of determination)，中文翻译为“决定系数”或者“拟合优度”，反映的是模型拟合数据的准确程度

一般R² 的范围是0到1：
1）越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好
2）越接近0，表明模型拟合的越差

R2=$\frac{SSR}{SST}=1-\frac{SSE}{SST}$

其中：SST=SSR+SSE
SST(total sum of squares)为总离差平方和，SST = $\sum (y_{i实际}-{\bar{y}}_{i实际}{)}^2$
实际每个y值，与实际y均值之差的平方和：表示实际数据的均值波动水平
SST越大，则实际数据本身波动越大
SST越小，则实际数据本身波动越小

SSR(regression sum of squares)为回归平方和，SSR = $\sum (y_{i计算}-{\bar{y}}_{i实际}{)}^2$
计算出的每个y值，与实际y均值之差的平方和

SSE(error sum of squares) 为残差平方和，SSE = $\sum (y_{i计算}-y_{i实际}{)}^2$
计算出的每个y值，与实际对应的每个y值之差的平方和（实际就是最小二乘法计算得到的）：表示计算数据与实际数据的误差波动水平
SSE越大，则计算数据与实际数据拟合程度较差。
SSE越小，则计算数据与实际数据拟合程度较好。
SSE本可以作为最小二乘法中损失函数值，但由于缺少对比，因此SSE到底要多小，才能认为拟合程度较好呢？？？

所以，R²引入 SST，与SSE能够对比衡量，$R^2=1-\frac{SSE}{SST}$

当 SSE 远远小于 SST 时，则 R² 越接近 1 ，表示计算数据与实际数据的误差波动，远远小于实际数据本身的波动。

这就像是，无论你上刀山还是下火海，波峰还是波谷，我都摸透了你的路数，每次掐指一算都能准确猜到你的下一步先迈左脚还是右脚，醒来是先睁眼还是先起身——一个拟合程度好的模型表示：我太懂你了！

当 SSE 与 SST 差距越小时，则 R² 越接近 0 ，表示计算数据与实际数据的误差波动，与实际数据本身的波动相差不大。
实际数据本身的波动SST，是实际数据跟实际均值作比较的，实际数据是有波动的，实际均值就是一条水平线（没有波动）。
计算数据与实际数据的误差波动SSE，是实际数据与计算数据作比较的，实际数据是有波动的，那计算数据是否与实际数据波动相似呢？

如果SSE与SST接近，则说明，计算数据的值相当于实际均值（没有波动），说明计算数据与波动的实际数据，拟合效果并不好。

这就像是，无论你上刀山还是下火海，波峰还是波谷，我都无法跟随你的步子——一个拟合程度不好的模型表示：我不懂你，所以跟不上你的路数。

3.2 逻辑回归模型

模型分类\实际类别	0	1
0	✔	×
1	×	✔

3.2.1 分类准确率

分类准确率：正确分类的样本数，与总样本数之比

3.2.2 精确率、召回率、F1

精确率，是模型分类为某一类的结果中，该类结果的分类精确率 = $\frac{准确分类数}{准确分类数+错误分类数}$

例如，模型分类为男的样本数量为 100，但其中，这100个模型分类为男的结果中，
与实际类别相符的为80个（实际男，分类男），与实际类别不相符的为20个（实际女，分类男）
那么男性分类精确率 = 80/100

在支付宝人脸识别中，如果支付宝识别出是你本人，就允许你用支付宝花钱、借贷等。
那么，提升精确率就非常必要！！！
识别为你的精确率，就是在支付宝识别为你的结果中，识别正确的比率。——是不是很正要！！！识别为你的精确率如果太低，意味着什么呢？
意味着，别人的脸有较大概率，也会被支付宝识别出是你！！！
这与假设检验中的β错误，逻辑相通：原假设为假，却接受原假设

精确率一般在“不能犯错”的情况下，非常重要！！！

比如，你精确率太低，意味着模型分类的结果中，错误的情况很多：自动驾驶时，道路识别错误就完蛋了

召回率，是实际为某一类中，模型分类结果与实际结果相符的比率。

例如，实际性别为男性的样本有200个，模型对其分类时，
正确分类为男性的有150个，错误分类为女性的有50个，
那么召回率 = 150/200

在支付宝人脸识别中，如果支付宝在识别你时，如果识别正确，就允许你用支付宝花钱、借贷等，识别不正确就不允许你花钱、借贷。
提升召回率，在这种情况下，只是用户体验的问题，并不会有太大的犯错问题。
比如，召回率低，意味着支付宝在识别你时，经常无法识别出是你，你就无法花支付宝的钱。——这时，你只是生个气，但财产没损失呀！
召回率高，意味着支付宝在识别你时，经常能识别出是你，你的用户体验就会比较好！
这与假设检验中的α错误，逻辑相通：原假设为真，却拒绝原假设

但召回率在某些“不能错过”的情况下，非常重要！！！

比如，你召回率太低，意味着实际某种情况的数量很多，但模型都没准确分类出来：比如自动驾驶时，实际有很多拐弯的道路，如果模型识别不出来，岂不是很可怕！

F1 分数，是精确率和召回率的调和平均。

F1 = $\frac{2\ast 精确率\ast 召回率}{精确率+召回率}$

困惑：为什么F1是精确率和召回率的调和平均呢？

为什么就不能是 F1 = 0.5精确率+0.5召回率

即使看了很多解释，感觉还缺点儿什么，还是用自己的理解吧。

	实际男	实际女	分类汇总
分类男	30	a1-50	a1-20
分类女	a0-30	50	a0+20
实际汇总	a0	a1	a0+a1

当实际数据类别中，总人数确定时，a1 = 总人数-a0

如果实际男a0远远小于实际女a1，精确率 = $\frac{30}{a0}$，召回率 = $\frac{30}{a1-20}$= $\frac{30}{总人数-a0-20}$，精确就会高于召回率

这种由于实际数据分类的不均匀，会导致精确率、召回率的相对不均匀

因此，应该先进行倒数计算为 $\frac{1}{精确率}=\frac{a0}{30}$，$\frac{1}{召回率}=\frac{a1-20}{30}$

将俩倒数相加后 除以 2 =（$\frac{a0}{30}+\frac{a1-20}{30}$）÷2

这样，实际a0与a1不均匀导致俩率不均匀问题就被消除了，再将其倒回来就成了F1

F1 = $\frac{2\ast 精确率\ast 召回率}{精确率+召回率}$

如果F1值越大，说明整体分类的效果较好。

4. 全流程总结

【极简流程，甚至不算科学严谨，但…能大致理解】

👉建立模型：根据任务类型（预测or分类），建立对应模型

预测定量数值：预测-线性回归模型

• 一元线性回归方程
• 多元线性回归方程

预测定类数据：分类-逻辑回归模型

• 二分类的逻辑回归方程-sigmoid函数
• 多分类的逻辑回归方程-softmax函数

👉 学习模型：求解模型最优状态下的参数W

1）明确衡量模型状态的指标，确定损失函数Loss

• 预测-线性回归模型的损失函数：最小二乘法
• 分类-逻辑回归模型的损失函数：极大似然估计法

2）求解计算指标最优的方式
求导解析解：

• 对Loss函数求W导，使导数为0，求出$W_{优}$

迭代近似解 ：

• ①设置W初始值
• ②明确W迭代方式：梯度下降法、牛顿法
• ③明确停止迭代方式：设置Loss阈值、设置迭代次数

👉 衡量模型：衡量最优状态下的模型效果

• 预测-线性回归模型：R²
• 分类-逻辑回归模型：准确率、精确率、召回率、F1分数

三、机器学习案例实现

多元线性回归_代码示例_sklearn实现
分类逻辑回归_代码示例_sklearn实现