时间序列分析 # 平稳AR模型和MA模型的识别与定阶

1. 掌握AR模型平稳性和MA模型可逆性的判别条件；
2. 掌握利用序列的自相关图和偏自相关图识别模型并进行初步定阶。

原始数据在文末！！！

练习1、根据某城市过去63年中每年降雪量数据（题目1数据.txt），求：

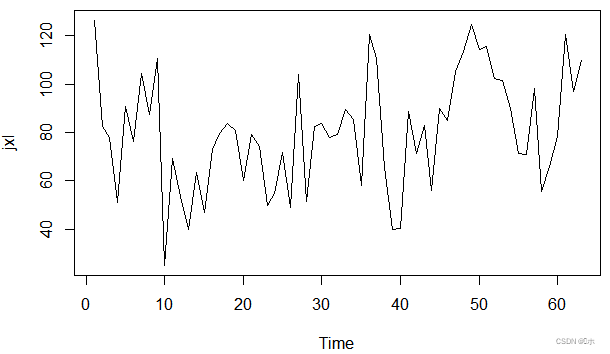
（1）绘制该序列的时序图，并对图形做出解释，判断该序列是否平稳；

（2）判断该序列的纯随机性；

（3）如果序列平稳且非白噪声，绘制样本自相关图（ACF）和偏自相关图（PACF），根据相关性特征，选择适当模型拟合该序列的发展。

setwd("C:/Users/Administrator/Desktop/实验4/习题数据")
#读入数据并绘制时序图
data1 <- scan("题目1数据.txt")
jxl <- ts(data1)
jxl
plot(jxl)
#白噪声检验
for (i in 1:2) print(Box.test(jxl,type = "Ljung-Box",lag = 6*i))
#绘制自相关图和偏自相关图
acf(jxl)
pacf(jxl)

结果分析：

（1）时序图显示，该序列始终在常数80附近波动，且波动范围有界。无明显的趋势性或周期性。该序列是平稳序列。

（2）延迟6阶的LB统计量的P值为0.03874小于α0.05，但是延迟12阶的LB统计量的P值为0.2474大于α0.05，则拒绝原假设，认为序列不是白噪声序列。