拉普拉斯变换（Fourie.Plus+）：通过引入衰减因子，让原函数图像在某种程度上“掰弯”，从而实现等幅震荡并满足傅里叶变换的计算要求

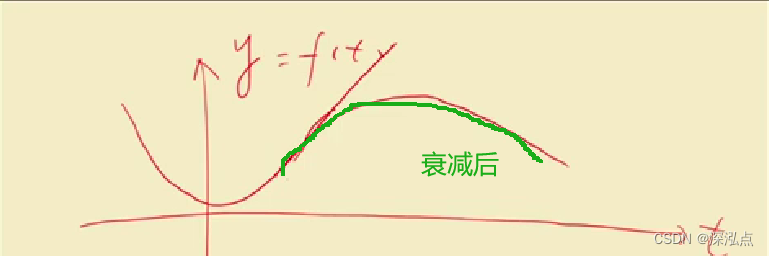
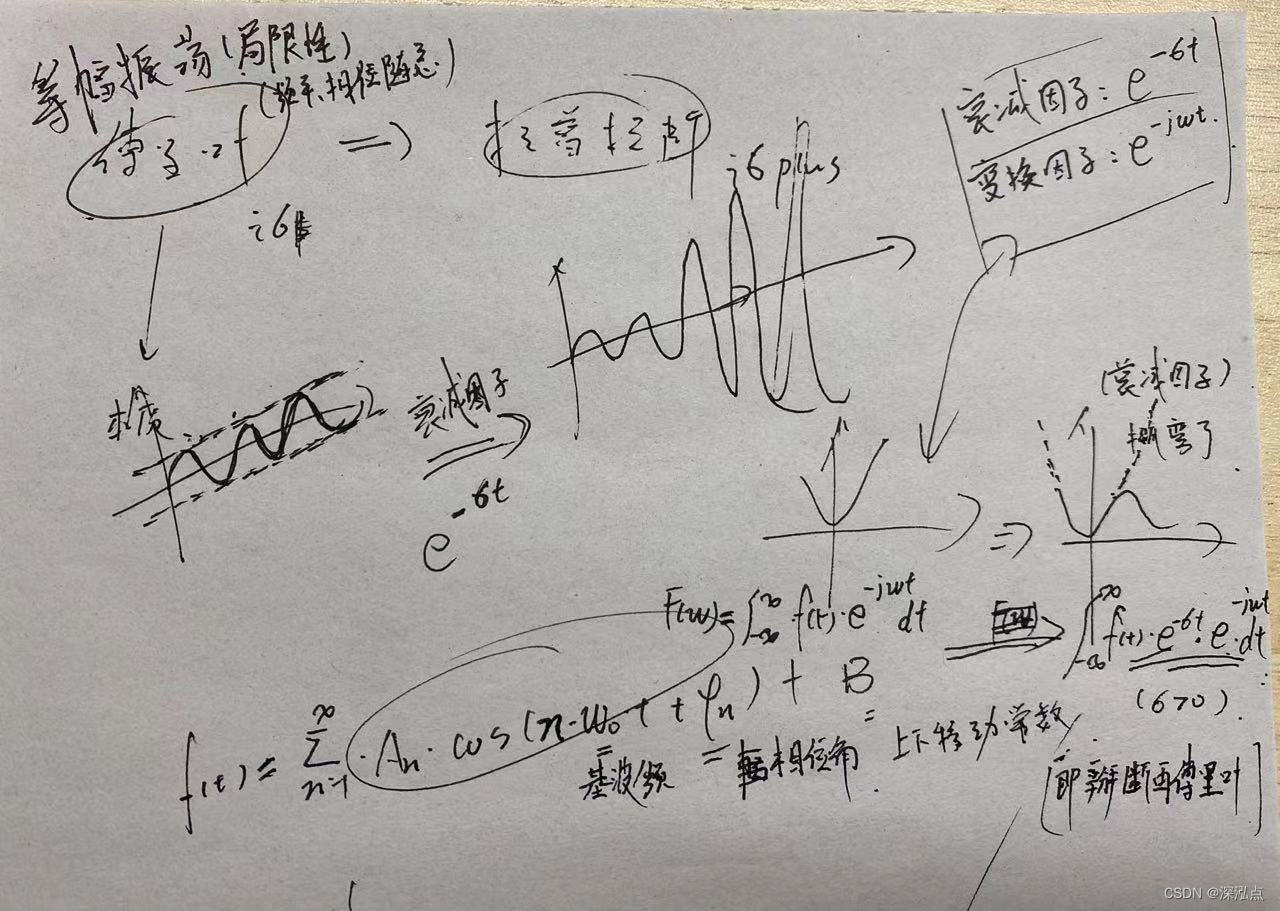
在处理一些在震荡同时幅度变得越来越大甚至趋于无限大的函数时，拉普拉斯变换通过引入衰减因子，使原函数的图像在某种程度上“掰弯”，从而实现等幅震荡，这样就能够满足傅里叶变换的计算要求。

拉普拉斯变换中的变量 s 实际上是引入衰减因子后的复数形式。傅里叶变换主要处理的是周期性函数，而拉普拉斯变换则适用于更广泛的情况，包括非周期性和增长型函数。

具体来说，拉普拉斯变换定义为：
L { f ( t ) } = F ( s ) = ∫ 0 ∞ f ( t ) e − s t d t \mathcal{L}\{f(t)\} = F(s) = \int_{0}^{\infty} f(t)e^{-st} dt L{f(t)}=F(s)=∫0∞​f(t)e−stdt
其中，$$s=\sigma +j\omega$$是复数【Tips：同，高中记的（ a + bi ) ，i 和 j 在数学和电学上都表示虚数单位（电气工程和物理学中，虚数单位通常表示为 j，以避免与电流表示的字母 i 混淆）】。

相比之下，傅里叶变换的定义为：
F { f ( t ) } = F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t \mathcal{F}\{f(t)\} = F(\omega) = \int_{-\infty}^{\infty} f(t)e^{-j\omega t} dt F{f(t)}=F(ω)=∫−∞∞​f(t)e−jωtdt

通过引入衰减因子$$e^{-\sigma t}$$，拉普拉斯变换可以处理那些傅里叶变换无法直接处理的函数。

附：收敛域（Region of Convergence, ROC）
是非常重要的一个概念。收敛域是指在复平面上拉普拉斯变换积分收敛的区域。具体来说，收敛域是使得积分
$${\int }_0^{\infty }f(t)e^{-st}dt$$
收敛的所有复数 s 的集合。

为了更好地理解这一点，我们可以考虑一个具体的例子。

假设有一个函数$$f(t)=e^{at}u(t)$$，其中$$u(t)$$是单位阶跃函数。

对这个函数进行拉普拉斯变换：
L { e a t u ( t ) } = ∫ 0 ∞ e a t e − s t d t = ∫ 0 ∞ e ( a − s ) t d t \mathcal{L}\{e^{at}u(t)\} = \int_{0}^{\infty} e^{at}e^{-st} dt = \int_{0}^{\infty} e^{(a-s)t} dt L{eatu(t)}=∫0∞​eate−stdt=∫0∞​e(a−s)tdt

为了使这个积分收敛，需要满足$$\mathrm{Re}(a-s)<0$$，也就是$$\mathrm{Re}(s)>a$$。

因此，对于函数$$e^{at}u(t)$$，其拉普拉斯变换的收敛域是$$\mathrm{Re}(s)>a$$。

总结来说，收敛域是拉普拉斯变换中非常关键的一部分，它决定了拉普拉斯变换存在的条件。不同的函数会有不同的收敛域，需要根据具体的函数形式进行分析。