三相电路分析

基本概念

相电压$U_p$：每相火线对中性线之间的电压
线电压$U_l$：每相火线之间的电压
相电流$I_p$：流经每相负载的电流
线电流$I_l$：流经每相火线的电流
对称三相电路：
相电压&线电压有：
$\underline{U_l}=\underline{U_p}\ast (\sqrt{3}\angle 30°)$
相电流&线电流有：
$\underline{I_l}=\underline{I_p}\ast (\sqrt{3}\angle -30°)$
(下划线表示是相量)

相序

a),正序
b),负序
c),零序

注意，线电压方向

对称三相电路计算

不对称三相电路计算

三相电路功率的计算

对称

$P=\sqrt{3}{U}_l{I}_{l}cos\phi$
$P=3U_p{I}_{p}cos\phi$
φ角是功率因数角，
是任意一相相电压和相电流的差角
不是线电压和线电流的差角
同理，有
$Q=\sqrt{3}{U}_l{I}_{l}sin\phi$
$Q=3U_p{I}_{p}sin\phi$
$S=\sqrt{3}{U}_l{I}_l$
$S=3U_p{I}_p$

不对称

提醒，关于不对称电路，将其当作复杂的时变电路分析即可，
电阻电路的一些分析方法依然适用
戴维南，诺顿，叠加，替代，回路电流，结点电压，电桥等等
功率不满足叠加定理
电路有功计算，只能计算出每相有功求和，
$P_{总}=P_A+P_B+P_C=U_{phA}{I}_{phA}cos{\phi }_A+U_{phB}{I}_{phB}cos{\phi }_B+U_{phC}{I}_{phC}cos{\phi }_C$
同理，无功也是
$Q_{总}=Q_A+Q_B+Q_C=U_{phA}{I}_{phA}sin{\phi }_A+U_{phB}{I}_{phB}sin{\phi }_B+U_{phC}{I}_{phC}sin{\phi }_C$
谨慎用电压电流关系直接相乘求得
不对称的三相电路只能下式计算
$S_{总}=\sqrt{P_{总}^2+Q_{总}^2}$
但
$S_{总}\ne U_{phA}{I}_{phA}+U_{phB}{I}_{phB}+U_{phC}{I}_{phC}$
表明不能用各相视在功率的叠加求总的视在功率

三相功率的测量

三表法

两表法

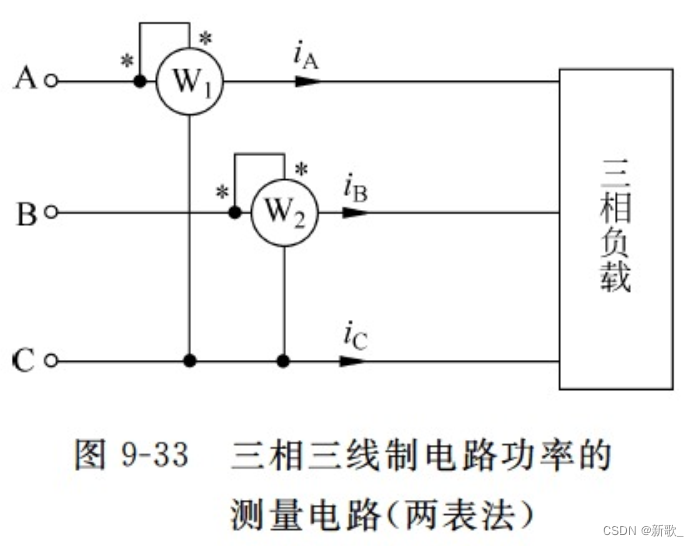
$P_{总}=P_1+P_2$
若是对称三相电路，就有
$Q_{总}=\sqrt{3}(P_1-P_2)$
$\phi =arctan\frac{Q_{总}}{P_{总}}=arctan(\frac{\sqrt{3}(P_1-P_2)}{P_1+P_2})$

对称三相电路一表法

测无功

测有功

由于线路是对称的，所以只需测出一相有功P×3即可

经典电路

裂相电路

$tan30°=\frac{X_{C1}}{R_1}=\frac{1}{\sqrt{3}}$
$tan60°=\frac{X_{C2}}{R_2}=\sqrt{3}$
即
$R_1=\sqrt{3}{X}_{C1}$
$X_{C2}=\sqrt{3}{R}_1$

同理，我们可以根据位形图，推出，
电感&电阻组合的裂相电路
电感、电容、电阻组合的裂相电路
不一一赘述

相序仪

三角函数

诱导公式记忆口诀：“奇变偶不变，符号看象限”。
“奇、偶”指的是π/2的倍数的奇偶，“变与不变”指的是三角函数的名称的变化：“变”是指正弦变余弦，正切变余切。（反之亦然成立）“符号看象限”的含义是：把角α看做锐角，不考虑α角所在象限，看n·(π/2)±α是第几象限角，从而得到等式右边是正号还是负号。
以cos（π/2+α）=－sinα为例，等式左边cos（π/2+α）中n=1，所以右边符号为sinα，把α看成锐角，所以π/2<（π/2+α）<π，y=cosx在区间（π/2，π）上小于零，所以右边符号为负，所以右边为－sinα。