三相四线制是一种电力系统配置，包括三根火线和一根零线，其中任意两火线间电压为380伏，火线与零线间电压为220伏。在低压配电网中，三相四线制常用于传输电能，零线通常不承载电流。颜色编码为A线黄色，B线绿色，C线红色，N线淡蓝色。在单相电应用中，使用火线和零线，零线有电流通过。遵循标准导线颜色编码能确保安全操作。
三相四线制
概述
1、三相四线是指三根火线和一根零线，正规叫法应该是三根相线和一根中线。
2、任意两根火线间的电压互为380伏。
3、任意火线和零线间的电压为220伏。
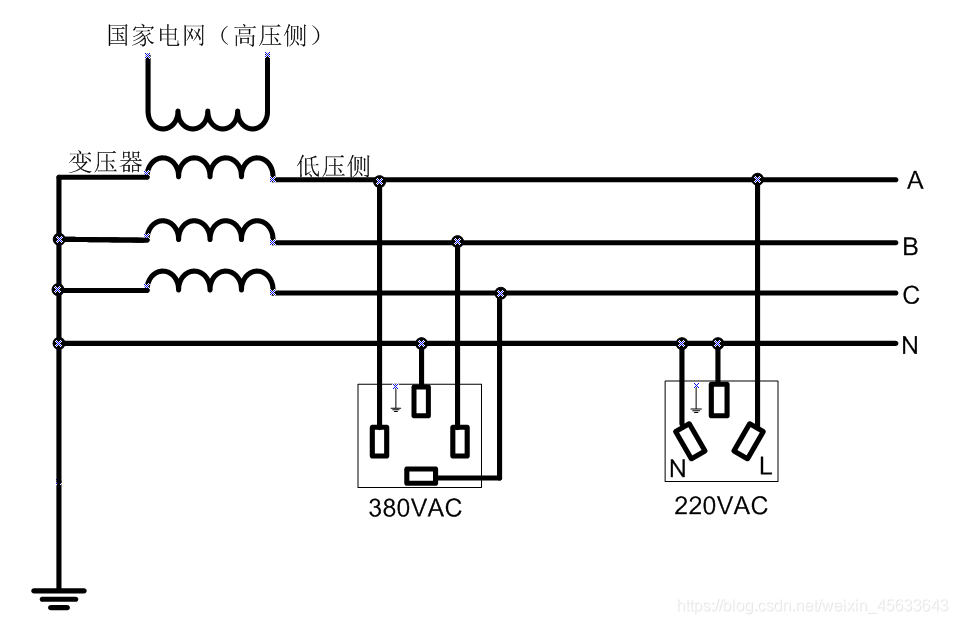
常见的三相电插座和单相电插座
三相(380VAC)：
单相（220VAC）
三相四线中最下面一根为零线，在低压配电网中，输电线路一般采用三相四线制，其中：
1、三条线路分别代表A，B，C三相，另一条是中性线N。
2、颜色分别表示为（红绿黄蓝）区别于零线。
3、在进入用户的单相输电线路中，有两条线，一条我们称为火线，另一条我们称为零线。
4、零线正常情况下要通过电流以构成单相线路中电流的回路。
5、三相系统中，三相自成回路，正常情况下中性线是无电流的，称三相四线制。
6、应用中最好使用标准/规范的导线颜色：A线用黄色，B线用绿色，C线用红色，N线用淡蓝色，PE线用黄绿色
单相电进户示意图
扫一扫
2481
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
