【LQR算法学习】[视频参考B站DR_CAN]【Advanced控制理论】8.5_线性控制器设计_轨迹跟踪(Follow a Desired Path) 文字版

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

DR_CAN是我很喜欢的B站博主。本文的图片来自视频的截图。侵删。
DR_CAN出书了，《控制之美》，欢迎大家购书支持。
本文用于记录学习LQR算法的学习过程。

学习资源：【Advanced控制理论】8.5_线性控制器设计_轨迹跟踪(Follow a Desired Path)
【Advanced控制理论】8.5_线性控制器设计_轨迹跟踪(Follow a Desired Path)

---

一、动机？

这部分讲的是系统的开环平衡点是（0，0），所以我们可以控制u，使系统收敛于平衡点。


建立了以误差和角速度为状态变量的空间状态方程。此时开环系统的平衡点不是（0，0），所以控制器需要有如下两个作用。

1. 稳定系统。没啥说的，控制首先要稳定。
2. 调整平衡点。个人理解是准的要求。
   
   对比之前的（0，0）为平衡点的系统，发现多了三角号那一项，所以在输入中想办法抵消掉。所以新的输入如图。
   
   最后，得到的状态空间方程如图。平衡点也是我们期望的。

施加输入后，新的系统的平衡点变为（0，0）。我们控制器设计的第二个目标达成。
然后再让特征值的实部小于0，就可以达到稳定的目的。这里是直接给了-1。
? 这里可以使用cost function来确定特征值吗？

二、simmulink仿真

matlab/simulink仿真

可爱的状态空间方程

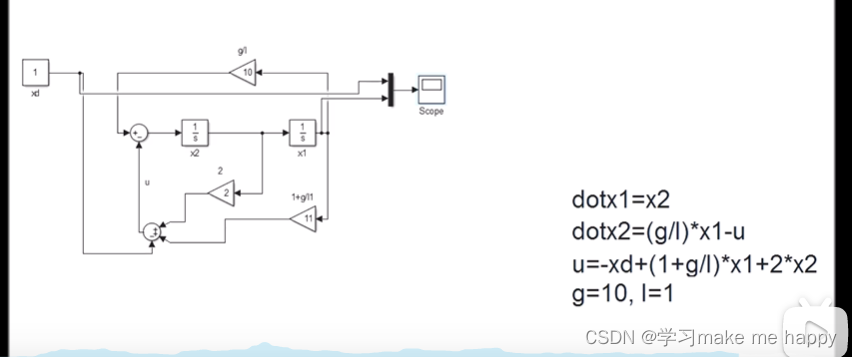
如下是上一节的图，可以对比着看一下。

上节内容结束。

输入为固定值时的响应。

为啥本节的主题是轨迹跟踪，给一个变换的输入。

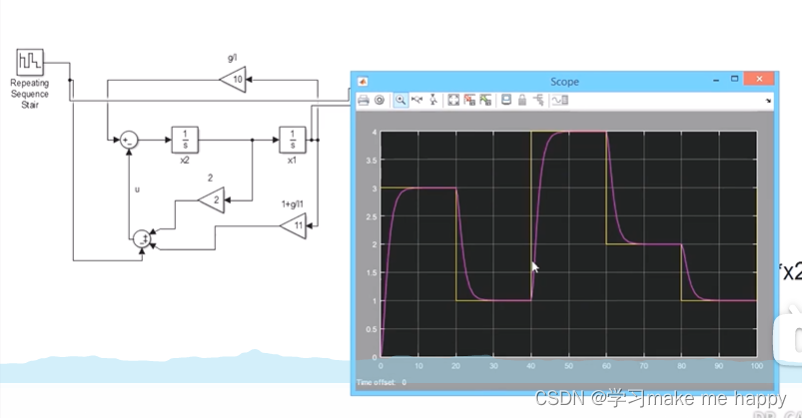
复杂的路线，还需要非线性的控制。<头疼>

总结

感谢DR_CAN提供的讲解。