stats | 使用（偏）自相关函数判断ARMA模型的阶数

自回归移动平均（autoregressive moving-averge，ARMA）模型是时间序列分析中常用的方法。它由自回归和移动平均两部分构成。

阶自回归过程：

• 其中， 。

阶移动平均过程：

• 其中，。

自回归移动平均模型：

• AR()、MA()过程分别可以看作是和时的特例。

判断ARMA模型的阶数一般使用自相关函数（ACF）和偏自相关函数（PACF）；自相关系数和偏自相关系数分别使用和表示。

判断的标准如下：

• 当和均不为0时，ACF和PCF呈现拖尾分布：

  • ACF：，从时开始衰减（可能直接，也可能震荡）；

  • PACF：从时开始衰减（可能直接，也可能震荡）。

• 当和时其中一个为0时：

  • 时为纯AR过程，PACF呈截尾分布，即在时为波峰（可正可负），之后为0；

  • 时为纯MA过程，ACF呈截尾分布，即在时为波峰（可正可负），之后为0。

上述两个函数在R语言中对应的函数分别是stats工具包中的acf()和pacf()。

AR(2)过程

set.seed(123)
p = rnorm(200)
y1 = rep(0,200)
for(i in c(3:200)){
  y1[i] = 0.7*y1[i-1] - 0.49*y1[i-2] + p[i]
}

layout(
  matrix(c(1,1,2,3), 2, byrow = T)
)
plot(y1[51:200], type = "l")
acf(y1[51:200])
pacf(y1[51:200])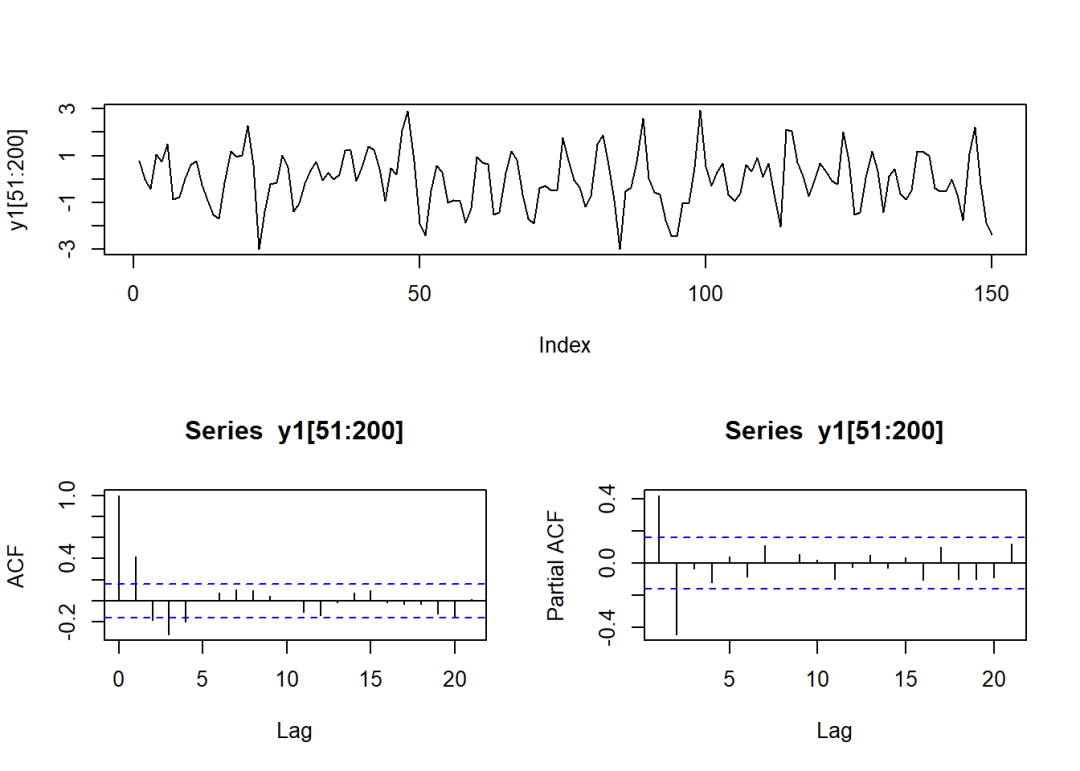

• 蓝色虚线内的值可以认为是不显著区别于0；

• ACF特征：拖尾分布；从起点处就开始震荡衰减；

• PACF特征：截尾分布；在处取得波峰（负峰），之后为0。

MA(1)过程

set.seed(456)
p = rnorm(200)
y2 = rep(0,200)
for(i in c(4:200)){
  y2[i] = p[i] - 0.7*p[i-1]
}

layout(
  matrix(c(1,1,2,3), 2, byrow = T)
)
plot(y2[51:200], type = "l")
acf(y2[51:200])
pacf(y2[51:200])

• ACF特征：截尾分布；在时取得波峰（负峰），之后为0；

• PACF特征：拖尾分布；从起点处就开始衰减。

ARMA(3,2)过程

set.seed(123)
p = rnorm(200)
y3 = rep(0,200)
for(i in c(4:200)){
    y3[i] = 0.2*y3[i-1] - 0.1*y3[i-2] + 0.5*y3[i-3] + p[i] + 0.2*p[i-1] - 0.7*p[i-2]
}

layout(
  matrix(c(1,1,2,3), 2, byrow = T)
)
plot(y3[51:200], type = "l")
acf(y3[51:200])
pacf(y3[51:200])

• ACF特征：拖尾分布；从处开始衰减（不明显）；

• PACF特征：拖尾分布；从处开始衰减（实际应为）。

使用（偏）自相关函数只能对ARMA模型的阶数作大致的判断，之后需要对系数进行估计和显著性检验来进行最终的判断。