day14 python shap可视化

参考帖子：SHAP 可视化解释机器学习模型简介_shap图-CSDN博客

今日任务
1．参考上述文档补全剩余的几个图
2．尝试确定一下shap各个绘图函数对于每一个参数的尺寸要求
3．确定分类问题和回归问题的数据如何才能满足尺寸，分类采取信贷数据集，回归采取单车数据集。

# 先运行之前预处理好的代码

import pandas as pd    #用于数据处理和分析，可处理表格数据。
import numpy as np     #用于数值计算，提供了高效的数组操作。
import matplotlib.pyplot as plt    #用于绘制各种类型的图表
import seaborn as sns   #基于matplotlib的高级绘图库，能绘制更美观的统计图形。
import warnings
warnings.filterwarnings("ignore")
 
 # 设置中文字体（解决中文显示问题）
plt.rcParams['font.sans-serif'] = ['SimHei']  # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False    # 正常显示负号
data = pd.read_csv('data.csv')    #读取数据


# 先筛选字符串变量 
discrete_features = data.select_dtypes(include=['object']).columns.tolist()
# Home Ownership 标签编码
home_ownership_mapping = {
    'Own Home': 1,
    'Rent': 2,
    'Have Mortgage': 3,
    'Home Mortgage': 4
}
data['Home Ownership'] = data['Home Ownership'].map(home_ownership_mapping)

# Years in current job 标签编码
years_in_job_mapping = {
    '< 1 year': 1,
    '1 year': 2,
    '2 years': 3,
    '3 years': 4,
    '4 years': 5,
    '5 years': 6,
    '6 years': 7,
    '7 years': 8,
    '8 years': 9,
    '9 years': 10,
    '10+ years': 11
}
data['Years in current job'] = data['Years in current job'].map(years_in_job_mapping)

# Purpose 独热编码，记得需要将bool类型转换为数值
data = pd.get_dummies(data, columns=['Purpose'])
data2 = pd.read_csv("data.csv") # 重新读取数据，用来做列名对比
list_final = [] # 新建一个空列表，用于存放独热编码后新增的特征名
for i in data.columns:
    if i not in data2.columns:
       list_final.append(i) # 这里打印出来的就是独热编码后的特征名
for i in list_final:
    data[i] = data[i].astype(int) # 这里的i就是独热编码后的特征名



# Term 0 - 1 映射
term_mapping = {
    'Short Term': 0,
    'Long Term': 1
}
data['Term'] = data['Term'].map(term_mapping)
data.rename(columns={'Term': 'Long Term'}, inplace=True) # 重命名列
continuous_features = data.select_dtypes(include=['int64', 'float64']).columns.tolist()  #把筛选出来的列名转换成列表
 
 # 连续特征用中位数补全
for feature in continuous_features:     
    mode_value = data[feature].mode()[0]            #获取该列的众数。
    data[feature].fillna(mode_value, inplace=True)          #用众数填充该列的缺失值，inplace=True表示直接在原数据上修改。

# 最开始也说了 很多调参函数自带交叉验证，甚至是必选的参数，你如果想要不交叉反而实现起来会麻烦很多
# 所以这里我们还是只划分一次数据集
from sklearn.model_selection import train_test_split
X = data.drop(['Credit Default'], axis=1)  # 特征，axis=1表示按列删除
y = data['Credit Default'] # 标签
# 按照8:2划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  # 80%训练集，20%测试集

from sklearn.ensemble import RandomForestClassifier #随机森林分类器

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score # 用于评估分类器性能的指标
from sklearn.metrics import classification_report, confusion_matrix #用于生成分类报告和混淆矩阵
import warnings #用于忽略警告信息
warnings.filterwarnings("ignore") # 忽略所有警告信息
# --- 1. 默认参数的随机森林 ---
# 评估基准模型，这里确实不需要验证集
print("--- 1. 默认参数随机森林 (训练集 -> 测试集) ---")
import time # 这里介绍一个新的库，time库，主要用于时间相关的操作，因为调参需要很长时间，记录下会帮助后人知道大概的时长
start_time = time.time() # 记录开始时间
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train) # 在训练集上训练
rf_pred = rf_model.predict(X_test) # 在测试集上预测
end_time = time.time() # 记录结束时间

print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
print("\n默认随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred))
print("默认随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred))

运行结果：

---

SHAP 原理简介

目标： 理解复杂机器学习模型（尤其是“黑箱”模型，如随机森林、梯度提升树、神经网络等）为什么会对特定输入做出特定预测。 SHAP 提供了一种统一的方法来解释模型的输出。

核心思想：合作博弈论中的 Shapley 值

SHAP (SHapley Additive exPlanations) 的核心基于博弈论中的 Shapley 值概念。想象一个合作游戏：

1. 玩家 (Players): 模型的特征 (Features) 就是玩家。
2. 游戏 (Game): 目标是预测某个样本的输出值。
3. 合作 (Coalition): 不同的特征子集可以“合作”起来进行预测。
4. 奖励/价值 (Payout/Value): 某个特征子集进行预测得到的值。
5. 目标： 如何公平地将最终预测结果（相对于平均预测结果的“收益”）分配给每个参与的特征（玩家）？

Shapley 值的计算思路（概念上）：

为了计算一个特定特征（比如“特征 A”）对某个预测的贡献（它的 Shapley 值），SHAP 会考虑：

1. 所有可能的特征组合（子集/联盟）： 从没有特征开始，到包含所有特征。
2. 特征 A 的边际贡献： 对于每一个特征组合，比较“包含特征 A 的组合的预测值”与“不包含特征 A 但包含其他相同特征的组合的预测值”之间的差异。这个差异就是特征 A 在这个特定组合下的“边际贡献”。
3. 加权平均： Shapley 值是该特征在所有可能的特征组合中边际贡献的加权平均值。权重确保了分配的公平性。

SHAP 的关键特性 (加性解释 - Additive Explanations):

SHAP 的一个重要特性是加性 (Additive)。这意味着：

• 基准值 (Base Value / Expected Value): 这是模型在整个训练（或背景）数据集上的平均预测输出。可以理解为没有任何特征信息时的“默认”预测。
• SHAP 值之和： 对于任何一个样本的预测，所有特征的 SHAP 值加起来，再加上基准值，就精确地等于该样本的模型预测值。

  模型预测值(样本 X) = 基准值 + SHAP值(特征1) + SHAP值(特征2) + ... + SHAP值(特征N)

为什么会生成 shap_values 数组？

根据上述原理，SHAP 需要为每个样本的每个特征计算一个贡献值（SHAP 值）：

1. 解释单个预测： SHAP 的核心是解释单个预测结果。
2. 特征贡献： 对于这个预测，我们需要知道每个特征是把它往“高”推了，还是往“低”推了（相对于基准值），以及推了多少。
3. 数值化： 这个“推力”的大小和方向就是该特征对该样本预测的 SHAP 值。

因此：

• 对于回归问题：

  • 模型只有一个输出。
  • 对 n_samples 个样本中的每一个，计算 n_features 个特征各自的 SHAP 值。
  • 这就自然形成了形状为 (n_samples, n_features) 的数组。 shap_values[i, j] 代表第 i 个样本的第 j 个特征对该样本预测值的贡献。

• 对于分类问题：

  • 模型通常为每个类别输出一个分数或概率。
  • SHAP 需要解释模型是如何得到每个类别的分数的。
  • 因此，对 n_samples 个样本中的每一个，分别为每个类别计算 n_features 个特征的 SHAP 值。
  • 最常见的组织方式是返回一个列表，列表长度等于类别数。列表的第 k 个元素是一个 (n_samples, n_features) 的数组，表示所有样本的所有特征对预测类别 k 的贡献。
  • shap_values[k][i, j] 代表第 i 个样本的第 j 个特征对该样本预测类别 k 的贡献。

总结:

SHAP 通过计算每个特征对单个预测（相对于平均预测）的边际贡献（Shapley 值），提供了一种将模型预测分解到每个特征上的方法。这种分解对于每个样本和每个特征（以及分类问题中的每个类别）都需要进行，因此生成了我们看到的 shap_values 数组结构。

shap库可解释性分析

import shap
import matplotlib.pyplot as plt
 
# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(rf_model)
 
# 计算 SHAP 值（基于测试集），这个shap_values是一个numpy数组，表示每个特征对每个样本的贡献值
# 这里大家先知道这是个numpy数组即可，我们后面学习完numpy在来回头解读这个值
shap_values = explainer.shap_values(X_test) # 这个计算耗时

1.SHAP 特征重要性条形图

# --- 1. SHAP 特征重要性条形图 (Summary Plot - Bar) ---
print("--- 1. SHAP 特征重要性条形图 ---")
shap.summary_plot(shap_values[:, :, 0], X_test, plot_type="bar",show=False)  #  这里的show=False表示不直接显示图形,这样可以继续用plt来修改元素，不然就直接输出了
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()

2.SHAP 特征重要性蜂巢图

# --- 2. SHAP 特征重要性蜂巢图 (Summary Plot - Violin) ---
print("--- 2. SHAP 特征重要性蜂巢图 ---")
shap.summary_plot(shap_values[:, :, 0], X_test,plot_type="violin",show=False,max_display=10) # 这里的show=False表示不直接显示图形,这样可以继续用plt来修改元素，不然就直接输出了
plt.title("SHAP Feature Importance (Violin Plot)")
plt.show()
# 注意下上面几个参数，plot_type可以是bar和violin，max_display表示显示前多少个特征，默认是20个

3. SHAP 依赖图

print("--- 3. SHAP 依赖图 ---")
shap.dependence_plot('Monthly Debt', shap_values[:,:,0], X_test, 
                    display_features=X_test,
                    interaction_index='Credit Score',show=False)
plt.title("SHAP Dependence Plot")
plt.show()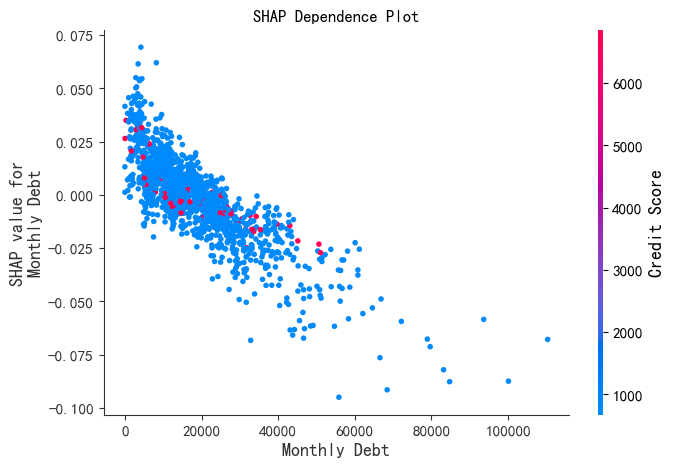

4. SHAP 力图

print("--- 4. SHAP 力图 ---")
shap.force_plot(explainer.expected_value[0],
                shap_values[:,:,0][0],
                X_test.iloc[0],
                matplotlib=True,
                show=False,
                text_rotation=30)
plt.title("SHAP Force Plot for Single Sample")
plt.show()

5. SHAP 决策图

print("--- 5. SHAP 决策图 ---")
shap.decision_plot(explainer.expected_value[0], 
                shap_values[:,:,0][50], 
                X_test.iloc[:50], 
                feature_order='hclust',
                show=False)
plt.title("SHAP Decision Plot")
plt.show()

重要提示：都知道shap_values是个三维数组，它这三个维度，分别对应着样本数量、特征数量，还有个额外维度。先看shap_values[:,:,0][0]，这里面这个0，它是从这个三维数组里，把第三个维度（也就是额外维度）的第一个切片给取出来。这么操作完，三维数组就变成二维的了。你就想象一个三层的书架，这个操作就像是只把最上面那一层书架拿出来，其他两层先不管。这个新得到的二维数组，每一行代表一个样本，每一列代表一个特征。再来说说后面那个0，也就是shap_values[:,:,0][0] 里的第二个0。前面不是已经得到一个二维数组了嘛，这个0就是从这个二维数组里选出第一行数据。这一选，二维数组就变成一维的了。打个比方，就像从刚才拿出来的那层书架上，只挑了第一本书。这 “一本书” 里存的，就是第一个样本在咱们前面选的那个额外维度切片下，所有特征的 SHAP 值。

如果按照shap_values[0][0]可能会出现shap_values的实际数据和形状不匹配的情况，我反复试验了好久一直找不到这个错误，但是在某些情况这样写可以的。还是要具体情况具体分析样本数量、特征数量。

@浙大疏锦行