【算法10】树状数组

1. 回顾一下前缀和数组：

基本性质：

• 首先我们知道前缀和数组初始化的时间复杂度是O(N)的，因为要遍历所有的元素
• 其次为什么要有前缀和？——因为方便了区间和的查询，时间复杂度为O(1)。

缺点和遗憾：
前缀和数组不好的一点是，他的**单点修改，时间复杂度是O(N)**的。因为一旦涉及到前面某一个点的修改，后续的前缀和都需要发生修改。

改进的想法：
我们发现查询的时间够快，但是修改和维护的速度太慢，成本太高。我们能不能舍弃一部分查询的速度，从而降低修改和维护的时间复杂度呢？

按照这个思路，我们会自然而然地想到分段求和。因为这样弱化了前缀和数组与原数组的关系，这个时候单点修改只需要维护某一段区间内的前缀和。但是代价是查询的时间复杂度变高。因为需要做一定的拼接。时间复杂度不再是O(1)了。可这种取舍，是值得的！

2. 分段求和的艺术：二进制表示法

前面已经明确了分段求和的思路，那么具体该怎么分段呢？十进制数的二进制表示法就是一个天然的分段规则。比如14=8+4+2，不就把前14个元素分成了三段了吗？

为什么说二进制是一种天然的分段规则，我想理由有两点：

1. 二进制能够表示所有的十进制整数下标
2. 这是我们唯二熟悉的进制。我们对位运算进行了大量的研究，有很多性质和规律可以供我们使用。

改进前缀和：
我们用c[i]来表示改进后的前缀和数组
1-----0001 1个1，只能分成一段：c[1] = a[1]
2-----0010 1个1，只能分成一段：c[2] = a[1] + a[2]
3-----0011 2个1，第一段c[2]已经维护，只需维护最新的一段：c[3] = a[3]
4-----0100 1个1，只能分成一段：c[4] = a[1] + a[2] + a[3] + a[4]
5-----0101 2个1，第一段c[4]已经维护，只需维护最新的一段：c[5] = a[5]
6-----0110 2个1，第一段c[4]已经维护，只需维护最新的一段：c[6] = a[5] + a[6]
7-----0111 3个1，前两段c[4]和c[2]已经维护，秩序维护最新的一段：c[7] = a[7]
8-----1000 1个1，只能分成一段：c[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8]
以此类推…

这里我们干了什么？

• 原本的前缀和数组s[i]是从a[1]一直加到a[i]。
• 改进后的前缀和数组c[i]就仅仅是：往前，下标所对应二进制的最后一个1的位权这么多个元素，相加的和。如果我们用 lowbit(i) 这个函数来代表下标所对应二进制的最后一个1的位权。那么c[i]就是前lowbit(i)项的和。

画个图可能会更加形象：

3. 树状数组

我们到这其实已经完成了树状数组的构建。我们再从下面这张图中感受一下树状数组的特点：

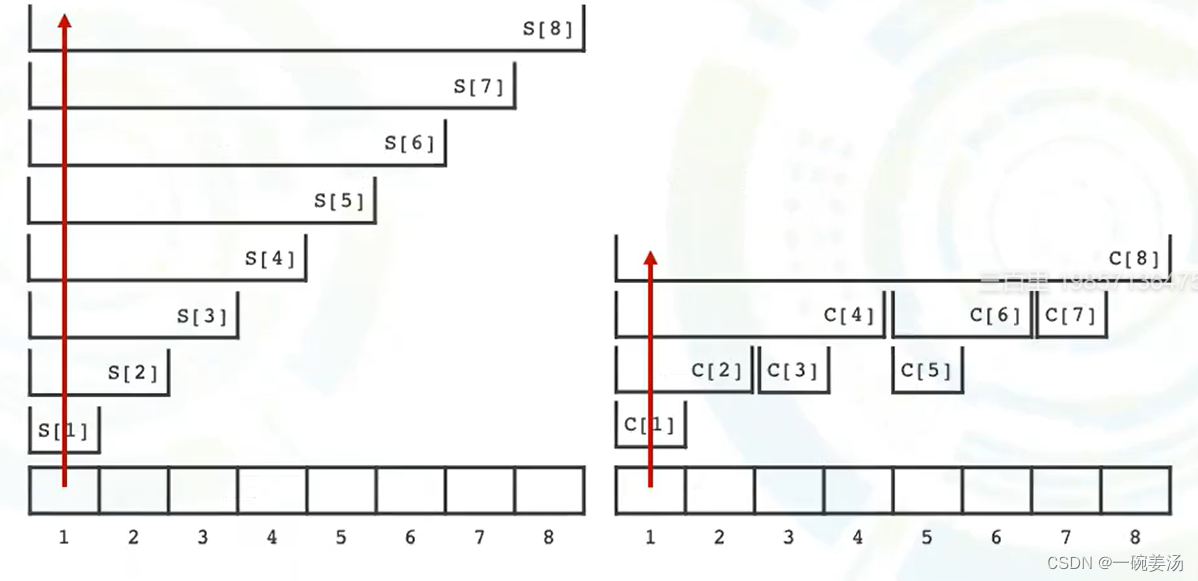
1. 扁平的树状结构使得单点修改的效率得到提升。修改了a[1]只需要修改c[1],c[2],c[4],c[8]，而不需要修改c[3],c[5]c[6],c[7]
2. 分段求和使得查询的效率降低：查询前7个元素的和=c[4] + c[6] + c[7]

基本操作

知道了它的分段求和规则以后，再来看树状数组的两个基本操作，是不是好理解了很多呢。（时间复杂度都是log(n)）

1. 前缀和查询： S[i] = S[i - lowbit(i)] + C[i] （向前统计）
2. 单点修改：A[j]发生改变时，当修改完C[j]，下一个应该修改的是C[j+lowbit[j]] （向后更新）

其中第二点似乎不太好理解，我们拿C[4]进行举例，为什么下一个要修改的元素是C[8]，而不是C[5],C[6]或者C[7]？因为只要C[j+k]中的k小于lowbit(j)，那么C[j+k]就不会包含C[j]，而当k=lowbit(j)的时候，C[j+k]就会包含C[j]区间
证明：
当k<lowbit(j)时：
lowbit(j+k)<=k
j+k - lowbit(j+k) >= j+k - k
j+k - lowbit(j+k) >= j

当k=lowbit(j)时：
lowbit(j+k)>k
j+k - lowbit(j+k) < j+k - k
j+k - lowbit(j+k) < j

lowbit(x)的计算：
x的二进制表示：xxxxx10000
x按位取反之后：x’x’x’x’x’01111
x按位取反再加1：x’x’x’x’x’10000
跟原来的二进制表示相与：0000010000
lowbit(x) = x & (-x)

代码模板：

#define MAX_N 100000
int c[MAX_N + 5];
inline int lowbit(int x) { return x & (-x); }
// 单点修改
void add(int x, int val, int n) { 
	while (x <= n) c[x] += val, x += lowbit(x);
}
// 查询
int query(int x) {
	int sum = 0;
	while (x) sum += c[x], x -= lowbit(x);
	return sum;
}

再来分享一道树状数组的经典例题：

• 操作C：区间加：差分优化，差分数组的两次单点修改。
• 操作Q：查询某个值：差分数组的前缀和。

代码：

#include<iostream>
using namespace std;
#define MAX_N 100000
int c[MAX_N + 5];
inline int lowbit(int x) { return x & (-x); }
void add(int x, int val, int n) {
    while (x <= n) c[x] += val, x += lowbit(x);
}
int query(int x) {
    int sum = 0;
    while (x) sum += c[x], x -= lowbit(x);
    return sum;
}
int main () {
    int n, pre = 0, now, m;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> now;
        add(i, now - pre, n);
        pre = now;
    }
    char str[10];
    cin >> m;
    for (int i = 0; i < m; i++) {
        cin >> str;
        switch (str[0]) {
            case 'C': {
                int a, b, c;
                cin >> a >> b >> c;
                add(a, c, n);
                add(b + 1, -c, n);
            } break;
            case 'Q': {
                int x;
                cin >> x;
                cout << query(x) << endl;
            } break;
        }
    }
    return 0;
}