【机器学习06】聚类基本概念

聚类是针对给定的样本，一句他们特征的相似度或距离，将其归并到若干个”类“或”簇“的数据分析问题。

一个类是样本的一个子集。直观上，相似的样本聚集在相同的类，不相似的样本分散在不同的类。

样本之间的相似度或距离起着重要作用。

相似度或距离

聚类的对象是观测数据，或样本集合。假设有n个样本，每个样本由m个属性的特征向量组成。样本集合可以用矩阵X表示：

1. 闵可夫斯基距离（样本 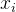 和  ）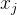

p=2时为欧氏距离；

p=1时为曼哈顿距离；

p=时为切比雪夫距离：(取各坐标数值差的绝对值的最大值)

2. 马哈拉诺比斯距离 / 马氏距离（样本 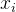 和  ）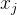

• S是协方差矩阵。

当S为单位矩阵时，即样本数据的各分量互相独立且各个分量的方差为1时，马氏距离就是欧氏距离。马氏距离是欧式距离的推广。

3. 相关系数

4. 夹角余弦（越接近1，越相似）

类或簇 ()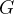

定义：

(1) 类的均值：

(2) 类的直径: 任意两样本之间的最大距离。

(3) 类的样本散步矩阵： 

(4) 类的样本协方差矩阵：

•  类与类之间的距离

  （1）最短距离或单连接：

        （2）最长距离或完全连接：

        （3）中心距离：

        （4）平均距离：