论文学习 DOLCE:AModel-Based Probabilistic Diffusion Framework for Limited-Angle CT Reconstruction

前言

论文连接
代码连接

省流

目标问题： 解决有限角度CT断层扫描的重建问题

具体问题：有限角度扫描进行重建后，重建的结果会有明显的伪影。

框架名称：DOLCE

具体方法：利用扩散模型作为图像的去噪器使用，去除伪影，数据一致性更新与扩散模型采样更新同步？不是很理解最后一句话。

相关描述

逆问题

对于CT重建的逆问题，实际上可以写作一个线性问题的逆。

我们定义$x\in R^n$为未知图像，$y\in R^m$为MRI，则线性方程可以描述为$$y=Ax$$

其中$A\in R^{m\times n}$，这实际上是一个不确定问题，因此往往需要更多的假设，才能使这个方程有唯一解。

DDPM

去噪扩散模型由一个确定性的前向过程，和一个参数化训练得到的反向过程组合。

前向过程按照如下公式进行:

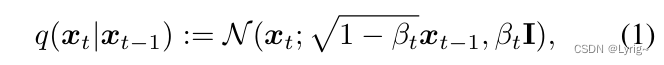
其中的${\beta }_t$是预先设定好的，随着$T$的不断增大，$x_t$最终会成为一个各向同性的高斯噪音。

改进的反向过程

反向过程遵循该公式，其中${\mu }_{\theta }$是参数化的神经网络预测的均值，这里需要说明的是，已经有论文证明，加上方差${\sigma }_t$的预测会使结果更加准确.

因此去噪过程的公式最终为：

DOLCE

文章采用了和DDPM相似的方法，但是添加了条件$c$，文章认为他们是第一个将条件生成用于CT重建的（这一点对此存疑）。

公式中的方差，文章采用生成的方式，即${\sigma }_t^2:={\sigma }_{\theta }^2(x_t,c,t)$

优化去噪模型

我们发现，通过预先构造低保真的图像作为条件，能够简化训练过程。目前主流的低保真的重建方法包含FBP和RLS，这里合适的选取时机，就需要各位战友们好好摸索一番了（不是），方法的选取主要取决于期望的重建质量以及运算效率，文章认为RLS方法有更高的GPU运行效率，且重建质量更好。

去噪模型的目标函数为：

这里需要说明，文章中添加条件的方式为，将条件$c$与前文RLS粗重建的图像，按照channel的维度进行合并。作为输入，进入模型。

这里还需要说明的是，在训练${\sigma }_{\theta }^2(x_t,c,t)$时，并不采取任何更多的约束，因为好像并不会有更多的性能提升。

此外，我们还采用随机条件训练的策略，对一个扩散模型同时采用条件与无条件两种推理方式，其选择概率为$p_{uncond}=0.2$，最终noise的预测采用加权的方式：

其中$\lambda$实际上是用于权衡两种噪音预测方式。

基于模型的迭代优化模式

迭代优化的第一步在于，利用传统inference阶段的过程，先重建一个${\hat{x}}_{t-1}$，只是这里采用的是条件模型预测得到的噪音。

其中$z\sim \mathcal{N}(0,I)$

之后，我们对于数据连续性的保证，采用近端优化策略：

其中的${\gamma }_t$用于权衡用于衡量数据连续性的$||Az-y|{|}_2^2$在式中所占比例。

当然，我们的模型也可以同时采用多个$x$并最终取平均值来代表。这种方法我们记作DOLCE-SA

实验结果

总结评价

需要格外注意 优化去噪模型 这一部分，方法太密集了，整篇论文的核心就在其中。