Diffusion（扩散模型）原理

–https://arxiv.org/abs/2006.11239
留意后续更新，欢迎关注微信公众号：组学之心

Diffusion（扩散模型）原理

扩散模型的相关工作大都起源于 OpenAI 于 2020 年提出的降噪扩散概率模型（Denoising Diffusion Probabilistic Models，DDPM）。DDPM 包含前向过程（Forward Process）和逆向过程（Reverse Process）

• 前向过程，称为扩散过程（Diffusion Process），本质上是在输入图像数据的基础上逐步注入符合高斯分布的随机噪声，直至图像数据本身变为服从标准高斯分布的随机噪声。
• 而逆向过程，则是进行图像生成的推断过程，当给定一个服从标准高斯分布的噪声，逐步去除噪声从而还原图像。

1. DDPM 前向过程

前向过程如图中的虚线箭头所示的 $q$ 过程，给定真实图像 ${\mathbf{x}}_0\sim q({\mathbf{x}}_0)$ 和 $T$ 个方差超参数 β = { β t ∈ ( 0 , 1 ) } t = 1 T \boldsymbol{\beta} = \{ \beta_t \in (0,1) \}_{t=1}^{T} β={βt​∈(0,1)}t=1T​，前向过程会逐步在图像中添加高斯噪声，得到图像集合 { x 1 , x 2 , . . . , x T } \{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_T\} {x1​,x2​,...,xT​}。

前向过程是马尔可夫过程

每个时刻的状态只与前一时刻的状态相关，因此前向过程是一个马尔可夫过程。以第 t 步为例，$t$ 仅与 $x_t$ 和 $x_{t-1}$ 相关，那么有:

$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I}\right)$$

$$q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$$

对于一个高斯分布 $\mathcal{N}(x;{\mu }_{\theta },{\sigma }_{\theta }^2\mathbf{I})$，如果要从中采样一个 $x$，利用重参数技巧，可以将采样写成：

$$x={\mu }_{\theta }+{\sigma }_{\theta }\odot ϵ,ϵ\sim \mathcal{N}(0,\mathbf{I})$$

因此，对于前向过程中的任意步骤的状态 $x_t$，可以表示为：

$$\begin{array}{rl}{x}_t& =\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{ϵ}_{t-1}\\ & =\sqrt{1-{\beta }_t}\left(\sqrt{1-{\beta }_{t-1}}{x}_{t-2}+\sqrt{{\beta }_{t-1}}{ϵ}_{t-2}\right)+\sqrt{{\beta }_t}{ϵ}_{t-1}\\ & =\sqrt{(1-{\beta }_t)(1-{\beta }_{t-1})}{x}_{t-2}+\sqrt{(1-{\beta }_t){\beta }_{t-1}}{ϵ}_{t-2}+\sqrt{{\beta }_t}{ϵ}_{t-1}\end{array}$$

其中，${ϵ}_{t-1},{ϵ}_{t-2}\sim \mathcal{N}(0,\mathbf{I})$。此外，对于两个独立的高斯分布 $\mathbf{X}\sim \mathcal{N}({\mu }_X,{\sigma }_X^2\mathbf{I})$ 与 $\mathbf{Y}\sim \mathcal{N}({\mu }_Y,{\sigma }_Y^2\mathbf{I})$，它们的和仍然服从高斯分布，即 $X+Y\sim \mathcal{N}({\mu }_X+{\mu }_Y,({\sigma }_X^2+{\sigma }_Y^2)\mathbf{I})$。

因此上述公式的后一项可写为：

$$\sqrt{(1-{\beta }_t){\beta }_{t-1}+{\beta }_t}{\overline{ϵ}}_{t-2},{\overline{ϵ}}_{t-2}\sim \mathcal{N}(0,\mathbf{I})$$

将其代回到原公式中，得到：

$$x_t=\sqrt{(1-{\beta }_t)(1-{\beta }_{t-1})}{x}_{t-2}+\sqrt{(1-{\beta }_t){\beta }_{t-1}+{\beta }_t}{\overline{ϵ}}_{t-2}$$

令 ${\alpha }_t=1-{\beta }_t$
${\bar{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$，代入上述式，得到：

$$\begin{array}{rl}{x}_t& =\sqrt{a_t{a}_{t-1}{x}_{t-2}}+\sqrt{a_t(1-a_{t-1})}+1-a_t{\overline{ϵ}}_{t-2}\\ & =\sqrt{a_t{a}_{t-1}{x}_{t-2}}+\sqrt{1-a_t{a}_{t-1}{\overline{ϵ}}_{t-2}}\\ & =\sqrt{{\bar{a}}_t}{x}_0+\sqrt{1-{\bar{a}}_t}{\overline{ϵ}}_0,{\overline{ϵ}}_{t-2},\dots ,{\overline{ϵ}}_0\sim \mathcal{N}(0,I)\end{array}$$

至此，可以发现在给定方差超参数集合 $\beta$ 的前提下，任意时刻的 $x_t$ 都可以使用 $x_0$ 和 $\beta$ 来表示，即：

$$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\bar{a}}_t}{x}_0,(1-{\bar{a}}_t)I)$$

其中，$a_t=1-{\beta }_t$，${\bar{a}}_t={\prod }_{i=1}^T{a}_i$， 且当 $T\to \infty$， ${\bar{a}}_t={\prod }_{i=1}^T{a}_i\to 0$， 从而 $x_T\sim \mathcal{N}(0,I)$。即当前向过程的步数趋于无穷大时，$x_T$ 最终将变为服从标准高斯分布的随机噪声。

如图所示为 DDPM 前向过程的简单示例，将 $T$ 设置为 100，方差超参数 ${\beta }_t$ 从 0.0001 递增到 0.1，可以发现当步数增多，原始图像也逐渐变得难以辨认直到完全变为随机噪声

2. DDPM 逆向过程

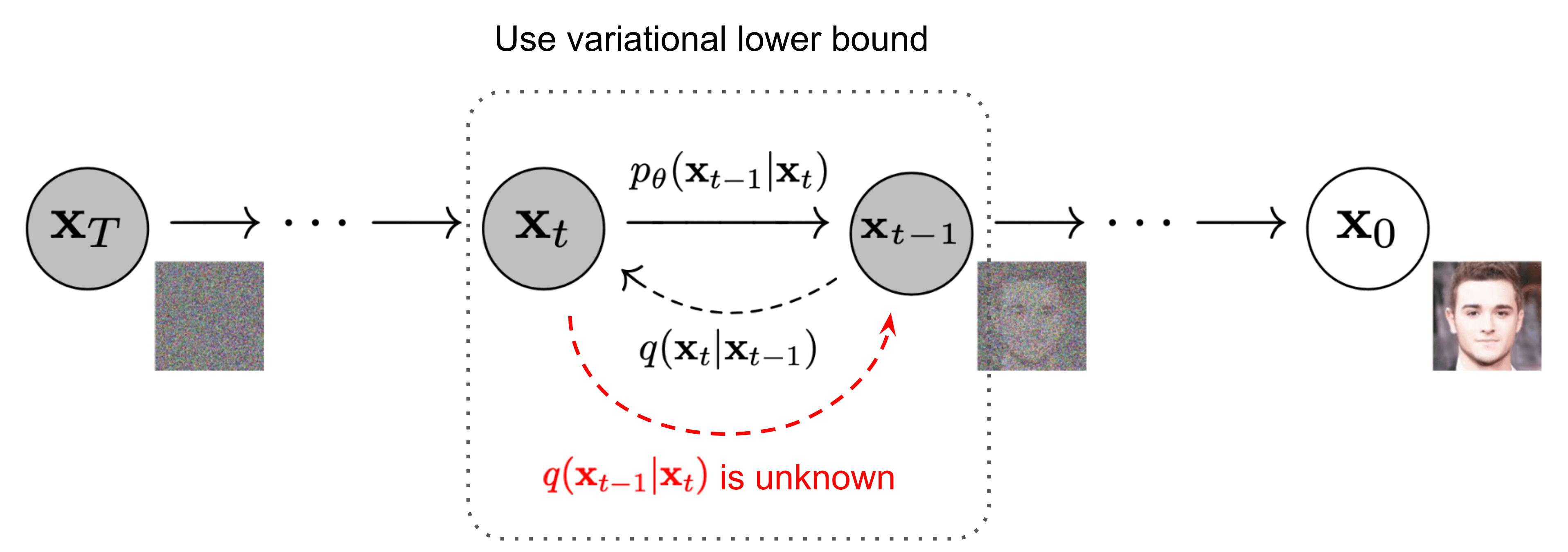
在前向过程中，通过 $q(x_t|x_{t-1})$ 逐步将真实图像 $x_0$ 变为标准高斯分布噪声 $x_T$；反之，如果可以获取前向过程每一步的真实逆向分布 $q(x_{t-1} | x_t) $，那也可以从一个标准高斯分布 $x_T$ 逐步去除噪声还原得到原始图像 $x_0$。

但实际上无法直接对真实逆向分布 $q(x_{t-1}|x_t)$ 进行推断，DDPM 使用神经网络 $p_{\theta }(x_{t-1}|x_t)$ 对逆向分布进行预测。

逆向分布 $p_{\theta }$ 可以表示为：

$$p_{\theta }(x_{0:T})=p_{\theta }(x_T)\prod _{t=1}^T{p}_{\theta }(x_{t-1}\mid x_t)$$

$$p_{\theta }(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))$$

逆向过程中的贝叶斯推理

DDPM 模型的目标则是学习到正确的 ${\mu }_{\theta }(x_t,t)$ 和 ${\Sigma }_{\theta }(x_t,t)$ 预测。虽然无法通过前向过程的分布 $q(x_t|x_{t-1})$ 去简单的推断出真实的逆向分布 $q(x_{t-1}|x_t)$，但是可以将 $x_0$（干净的图片数据）引入，根据贝叶斯公式，有：

$$q(x_{t-1}\mid x_t,x_0)=\frac{q(x_{t-1})q(x_0\mid x_{t-1})q(x_t\mid x_{t-1},x_0)}{q(x_0)q(x_t\mid x_0)}$$

$$=\frac{q(x_{t-1}\mid x_0)q(x_t\mid x_{t-1},x_0)}{q(x_t\mid x_0)}$$

将 $q(x_{t-1}\mid x_t,x_0)$ 的均值和方差表示为 ${\tilde{\mu }}_t(x_t,x_0)$ 和 ${\tilde{\beta }}_t$，即：

$$q(x_{t-1}\mid x_t,x_0)=\mathcal{N}(x_{t-1};{\tilde{\mu }}_t(x_t,x_0),{\tilde{\beta }}_{t}I)$$

逆向过程中的马尔科夫链推理

还记得刚刚提到前向过程是马尔可夫链吗？关键点是任一时间步的 $x_t$ 都可以使用 $x_0$ 和 $\beta$来表示，那么可以将(11)中的每一分项分别表示为如下形式：

$$q(x_t\mid x_{t-1},x_0)=q(x_t\mid x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$$

$$q(x_{t-1}\mid x_0)=\mathcal{N}(x_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}{x}_0,(1-{\bar{\alpha }}_{t-1})I)$$

$$q(x_t\mid x_0)=\mathcal{N}(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$$

化简$q(x_t\mid x_{t-1},x_0)$

对于一元高斯分布$x\sim \mathcal{N}(\mu ,{\sigma }^2)$，其概率密度函数为$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$。将上述每一分项高斯分布的概率密度函数的指数部分代入，有：

$$q(x_{t-1}\mid x_t,x_0)=\frac{q(x_{t-1}\mid x_0)q(x_t\mid x_{t-1},x_0)}{q(x_t\mid x_0)}$$

$$\propto \frac{\exp \left(-\frac{(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{)}^2}{2(1-{\bar{\alpha }}_{t-1})}\right)\exp \left(-\frac{(x_t-\sqrt{1-{\beta }_t}{x}_{t-1}{)}^2}{2{\beta }_t}\right)}{\exp \left(-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{2(1-{\bar{\alpha }}_t)}\right)}$$

$$=\exp \left(-\frac{1}{2}\left(\frac{(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}+\frac{(x_t-\sqrt{1-{\beta }_t}{x}_{t-1}{)}^2}{{\beta }_t}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}\right)\right)$$

$$=\exp \left(-\frac{1}{2}\left(\left(\frac{1}{1-{\bar{\alpha }}_{t-1}}+\frac{1-{\beta }_t}{{\beta }_t}\right)x_{t-1}^2-\left(2\frac{\sqrt{{\bar{\alpha }}_{t-1}}{x}_0}{1-{\bar{\alpha }}_{t-1}}+2\frac{\sqrt{1-{\beta }_t}{x}_t}{{\beta }_t}\right)x_{t-1}+C(x_t,x_0)\right)\right)$$

其中，$C(x_t,x_0)$为与$x_{t-1}$无关项的组合，可以忽略。此外，一元高斯分布概率密度函数的指数部分可以展开：

$$\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)=\exp \left(-\frac{1}{2}\left(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}\right)\right)$$

$\frac{1}{{\sigma }^2}$和$\frac{2\mu }{{\sigma }^2}$分别对应公式中的：

$$\frac{1}{{\tilde{\beta }}_t}=\left(\frac{1}{1-{\bar{\alpha }}_{t-1}}+\frac{1-{\beta }_t}{{\beta }_t}\right)=\frac{1-{\bar{\alpha }}_t}{(1-{\bar{\alpha }}_{t-1}){\beta }_t}$$

$$\frac{2{\tilde{\mu }}_t(x_t,x_0)}{{\tilde{\beta }}_t}=\left(2\frac{\sqrt{{\bar{\alpha }}_{t-1}}{x}_0}{1-{\bar{\alpha }}_{t-1}}+2\frac{\sqrt{1-{\beta }_t}{x}_t}{{\beta }_t}\right)$$

因此可以求得$q(x_{t-1}\mid x_t,x_0)$的均值${\tilde{\mu }}_t(x_t,x_0)$和方差${\tilde{\beta }}_t$：

$${\tilde{\mu }}_t(x_t,x_0)=\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t{x}_0+(1-{\bar{\alpha }}_{t-1})\sqrt{{\alpha }_t}{x}_t}{1-{\bar{\alpha }}_t},{\tilde{\beta }}_t=\frac{(1-{\bar{\alpha }}_{t-1}){\beta }_t}{1-{\bar{\alpha }}_t}$$

引入前向过程中已得到的$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}\overline{{ϵ}_0}$，$\overline{{ϵ}_0}\sim \mathcal{N}(0,I)$，可以得到$x_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left(x_t-\sqrt{1-{\bar{\alpha }}_t}\overline{{ϵ}_0}\right)$，代入上述公式中有：

$${\tilde{\mu }}_t(x_t,x_0)=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}\overline{{ϵ}_0}\right)$$

• 虽然去除了$x_0$的影响，但是引入了一个新的变量$\overline{{ϵ}_0}$，它在前向过程中为标准高斯分布采样的噪声，但是在逆向过程中无法得知其真实值，DDPM引入一个参数化的神经网络模型${ϵ}_{\theta }(x_t,t)$去预测噪声 $\overline{{ϵ}_0}$，$\theta$表示模型的参数。

现在已经可以确定DDPM需要学习的逆向过程$p_{\theta }(x_{t-1}\mid x_t)$的分布：

$$p_{\theta }(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))$$

其中：

$${\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)\right)$$

$${\Sigma }_{\theta }(x_t,t)={\tilde{\beta }}_t=\frac{(1-{\bar{\alpha }}_{t-1}){\beta }_t}{1-{\bar{\alpha }}_t}\approx {\beta }_t$$

• DDPM 逆向过程可总结为：在给定$x_t$的前提下，首先预测高斯噪声${ϵ}_{\theta }(x_t,t)$，然后计算$p_{\theta }(x_{t-1}\mid x_t)$的均值${\mu }_{\theta }(x_t,t)$和方差${\Sigma }_{\theta }(x_t,t)$，最后通过重参数技巧计算得到$x_{t-1}$完成一步推断，循环进行直至得到$x_0$。

3. DDPM 的损失函数设计

DDPM 使用最大似然估计作为优化目标，损失函数为：

$$L={\mathbb{E}}_{q(x_0)}[-\log p_{\theta }(x_0)]$$

应用变分下限 (Variational Lower Bound, VLB) 优化负对数似然，在原始损失函数$L$的基础上，引入一项KL散度$D_{KL}(q(x_{1:T}\mid x_0)\parallel p_{\theta }(x_{1:T}\mid x_0))$。KL散度的值非负，所以满足下列不等式：

$${\mathbb{E}}_{q(x_0)}[-\log p_{\theta }(x_0)]\le {\mathbb{E}}_{q(x_0)}[-\log p_{\theta }(x_0)+D_{KL}(q(x_{1:T}\mid x_0)\parallel p_{\theta }(x_{1:T}\mid x_0))]$$

其中，KL 散度的定义如下：

$$D_{KL}(q(x_{1:T}\mid x_0)\parallel p_{\theta }(x_{1:T}\mid x_0))=\sum q(x_{1:T}\mid x_0)\cdot \log \left(\frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{1:T}\mid x_0)}\right)$$

$$={\mathbb{E}}_{q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{1:T}\mid x_0)}\right]$$

将其代入到上述公式中，并应用贝叶斯公式进行化简，有：

$${\mathbb{E}}_{q(x_0)}[-\log p_{\theta }(x_0)]$$

$$\le {\mathbb{E}}_{q(x_0)}\left[-\log p_{\theta }(x_0)+{\mathbb{E}}_{q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{1:T}\mid x_0)}\right]\right]$$

$$={\mathbb{E}}_{q(x_0)}\left[-\log p_{\theta }(x_0)+{\mathbb{E}}_{q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})/p_{\theta }(x_0)}\right]\right]$$

$$={\mathbb{E}}_{q(x_0)}\left[-\log p_{\theta }(x_0)+{\mathbb{E}}_{q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})}+\log p_{\theta }(x_0)\right]\right]$$

$$={\mathbb{E}}_{q(x_0)}\left[{\mathbb{E}}_{q(x_{1:T}\mid x_0)}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})}\right]\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})}\right]=L_{VLB}$$

此时，DDPM 的优化目标可以从最小化$L$转换为最小化$L_{VLB}$，由前向过程和逆向过程的介绍可知$q(x_{1:T}\mid x_0)={\prod }_{t=1}^{T}q(x_t\mid x_{t-1})$，$p_{\theta }(x_{0:T})=p_{\theta }(x_T){\prod }_{t=1}^T{p}_{\theta }(x_{t-1}\mid x_t)$，代入上面的公式可进一步推导得出：

$$L_{VLB}$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{q(x_{1:T}\mid x_0)}{p_{\theta }(x_{0:T})}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{{\prod }_{t=1}^{T}q(x_t\mid x_{t-1})}{p_{\theta }(x_T){\prod }_{t=1}^T{p}_{\theta }(x_{t-1}\mid x_t)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[-\log p_{\theta }(x_T)+\sum _{t=1}^T\log \frac{q(x_t\mid x_{t-1})}{p_{\theta }(x_{t-1}\mid x_t)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[-\log p_{\theta }(x_T)+\sum _{t=2}^T\log \frac{q(x_t\mid x_{t-1})}{p_{\theta }(x_{t-1}\mid x_t)}+\log \frac{q(x_1\mid x_0)}{p_{\theta }(x_0\mid x_1)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[-\log p_{\theta }(x_T)+\sum _{t=2}^T\log \left(\frac{q(x_{t-1}\mid x_t,x_0)q(x_t\mid x_0)}{p_{\theta }(x_{t-1}\mid x_t)q(x_{t-1}\mid x_0)}\right)+\log \frac{q(x_1\mid x_0)}{p_{\theta }(x_0\mid x_1)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[-\log p_{\theta }(x_T)+\sum _{t=2}^T\log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta }(x_{t-1}\mid x_t)}+\sum _{t=2}^T\log \frac{q(x_t\mid x_0)}{q(x_{t-1}\mid x_0)}+\log \frac{q(x_1\mid x_0)}{p_{\theta }(x_0\mid x_1)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[-\log p_{\theta }(x_T)+\sum _{t=2}^T\log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta }(x_{t-1}\mid x_t)}+\log \prod _{t=2}^T\frac{q(x_t\mid x_0)}{q(x_{t-1}\mid x_0)}+\log \frac{q(x_1\mid x_0)}{p_{\theta }(x_0\mid x_1)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[-\log p_{\theta }(x_T)+\sum _{t=2}^T\log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta }(x_{t-1}\mid x_t)}+\log \frac{q(x_T\mid x_0)}{q(x_1\mid x_0)}+\log \frac{q(x_1\mid x_0)}{p_{\theta }(x_0\mid x_1)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{q(x_T\mid x_0)q(x_1\mid x_0)}{q(x_1\mid x_0)p_{\theta }(x_0\mid x_1)}\frac{1}{p_{\theta }(x_T)}+\sum _{t=2}^T\log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta }(x_{t-1}\mid x_t)}\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[\log \frac{q(x_T\mid x_0)}{p_{\theta }(x_T)}+\sum _{t=2}^T\log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta }(x_{t-1}\mid x_t)}-\log p_{\theta }(x_0\mid x_1)\right]$$

$$={\mathbb{E}}_{q(x_{0:T})}\left[D_{KL}(q(x_T\mid x_0)\parallel p_{\theta }(x_T))+\sum _{t=2}^T{D}_{KL}(q(x_{t-1}\mid x_t,x_0)\parallel p_{\theta }(x_{t-1}\mid x_t))-\log p_{\theta }(x_0\mid x_1)\right]$$

DDPM 对上述优化目标进行了简化，只考虑公式中计算分布$q(x_{t-1}\mid x_t,x_0)$与$p_{\theta }(x_{t-1}\mid x_t)$之间的KL散度部分：

$$q(x_{t-1}\mid x_t,x_0)=\mathcal{N}(x_{t-1};{\tilde{\mu }}_t(x_t,x_0),{\tilde{\beta }}_{t}I)$$

$$p_{\theta }(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_{-t},t),{\Sigma }_{\theta }(x_t,t))=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_{-t},t),{\tilde{\beta }}_{t}I)$$

因此：

$$L_t=D_{KL}(q(x_{t-1}\mid x_t,x_0)\parallel p_{\theta }(x_{t-1}\mid x_t))$$

$$=\left[\frac{1}{2{\beta }_t}\Vert {\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_{-t},t){\Vert }^2\right]$$

$$={\mathbb{E}}_{x_0,\overline{{ϵ}_0}}\left[\frac{1}{2{\beta }_t}\Vert \frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}\overline{{ϵ}_0}\right)-\frac{1}{\sqrt{{\alpha }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)\right){\Vert }^2\right]$$

$$={\mathbb{E}}_{x_0,\overline{{ϵ}_0}}\left[\frac{{\beta }_t^2}{2{\beta }_t{\alpha }_t(1-{\bar{\alpha }}_t)}\Vert \overline{{ϵ}_0}-{ϵ}_{\theta }(x_t,t){\Vert }^2\right]$$

$$={\mathbb{E}}_{x_0,\overline{{ϵ}_0}}\left[\frac{{\beta }_t^2}{2{\beta }_t{\alpha }_t(1-{\bar{\alpha }}_t)}\Vert \overline{{ϵ}_0}-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}\overline{{ϵ}_0},t){\Vert }^2\right]$$

DDPM 进一步对$L_t$进行简化，得到：

$$L_{simple}={\mathbb{E}}_{x_0,\overline{{ϵ}_0}}\left[\Vert \overline{{ϵ}_0}-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}\overline{{ϵ}_0},t){\Vert }^2\right]$$

由此可见：DDPM 最终损失函数的核心就是最小化采样的真实噪声$\overline{{ϵ}_0}$与模型所预测噪声${ϵ}_{\theta }$之间的均方误差损失。

下一篇推文来用代码实战一下怎么做一个DDPM模型。