基于智能优化算法实现自动泊车的路径动态规划（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

1. 问题定义

2. 智能优化算法应用

3. 动态规划方法

4. 环境感知与车辆运动模型

5. 安全性与约束条件

6. 仿真与实车测试

7. 用户体验与成本考量

📚2 运行结果

🎉3 参考文献

 🌈4 Matlab代码实现

---

💥1 概述

作为一种方便、快捷的交通工具，汽车已成为人们生活和工作的重要组成部分。随着汽车数量的逐年增加，有限的城市空间显得日趋拥挤，车辆平均分配到的停放空间也日趋缩小，车辆泊车入位困难问题在人们生活中逐渐显现。人们对车辆使用轻便性及安全性要求促使越来越多汽车生产商、科研机构及高校对泊车系统进行研究。目前，国外已有部分汽车生产商推出自己的自动泊车系统，但仅装配于高端车型，我国暂时还未具有自主知识产权的汽车自动泊车系统。因此，本文以低端车型为研究平台，针对自动平行泊车系统的核心技术——泊车控制策略进行探索，目的为提高泊车操作轻便性和泊车过程安全性。 本文采用泊车路径规划和泊车路径跟踪控制方法进行泊车系统控制器控制策略设计。

 本文旨在通过一个简单的脚本实现自动泊车的路径规划动态演示，并对泊车路线进行曲线拟合。

基于智能优化算法实现自动泊车的路径动态规划研究是一个结合了智能算法、自动化控制和车辆工程的跨学科领域，旨在通过高效寻找最佳泊车路径，提高自动泊车系统的可靠性和用户体验。以下是研究的关键方面和考虑因素：

1. 问题定义

自动泊车路径动态规划的目标是在给定的停车场环境中，考虑车辆尺寸、障碍物位置、车位位置及车辆运动约束（如转弯半径），自动规划出一条从当前位置到目标停车位的安全、高效的行驶路径。

2. 智能优化算法应用

• 遗传算法（GA）: 通过模拟自然选择和遗传机制搜索解空间，找到最佳或近似最佳的泊车路径。
• 粒子群优化（PSO）: 模拟鸟群觅食行为，通过粒子间的信息共享和迭代更新搜索最优路径。
• 模拟退火算法（SA）: 以金属退火过程为灵感，允许算法在搜索过程中“跳跃”出局部最优解，以求全局最优。
• 蚁群优化（ACO）: 借鉴蚂蚁觅食过程中信息素引导的路径选择机制，寻找最短或成本最低的路径。

3. 动态规划方法

结合上述智能优化算法与动态规划，考虑路径的分段优化，如将泊车路径分为几个阶段（如接近车位、转向对齐、倒车入库等），对每个阶段进行优化后再综合考虑全局路径，以解决复杂的泊车场景。

4. 环境感知与车辆运动模型

• 环境感知: 利用传感器（雷达、摄像头、超声波等）获取实时的车辆周边环境数据，包括障碍物位置、车位位置等。
• 车辆运动模型: 建立精确的车辆运动学和动力学模型，考虑车辆转向、加速、减速等动态特性，确保规划的路径可行。

5. 安全性与约束条件

确保规划路径满足车辆操作的安全约束，如最小转弯半径、避免碰撞、保持与障碍物的安全距离等。同时，考虑实时交通规则和泊车规定。

6. 仿真与实车测试

• 仿真验证: 利用MATLAB/Simulink、CarSim等工具进行软件仿真，验证算法的有效性、路径的可行性及系统的稳定性。
• 实车测试: 在封闭或指定测试场进行实地试验，评估自动泊车系统的实际表现，收集数据反馈优化算法。

7. 用户体验与成本考量

研究中还需考虑用户界面的友好性、操作便捷性及系统成本，确保技术的商业化推广潜力。

综上所述，基于智能优化算法的自动泊车路径动态规划研究是一个综合技术挑战与市场应用潜力并存的领域，需跨学科合作，不断推进算法的优化、系统集成及实际应用。

📚2 运行结果

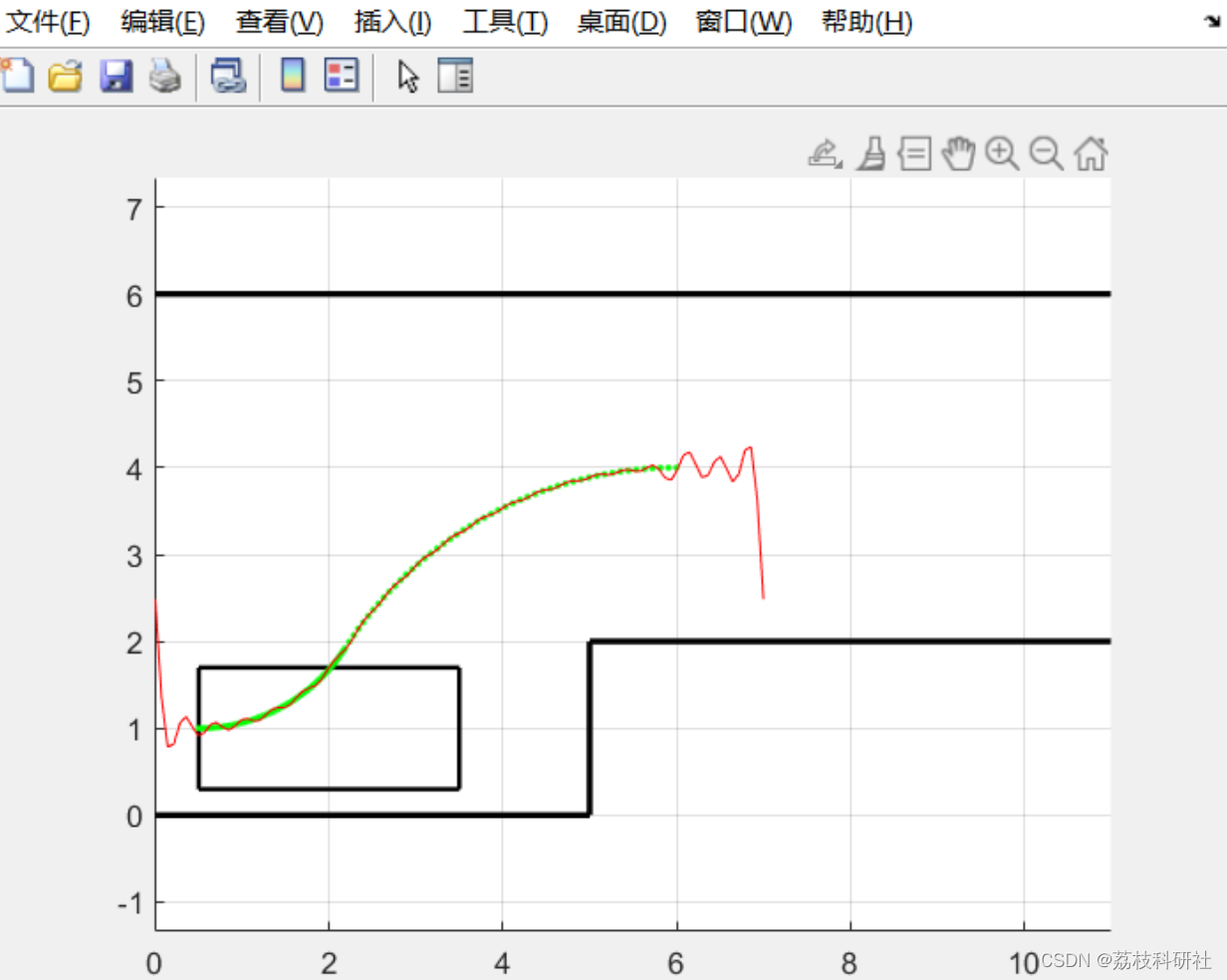
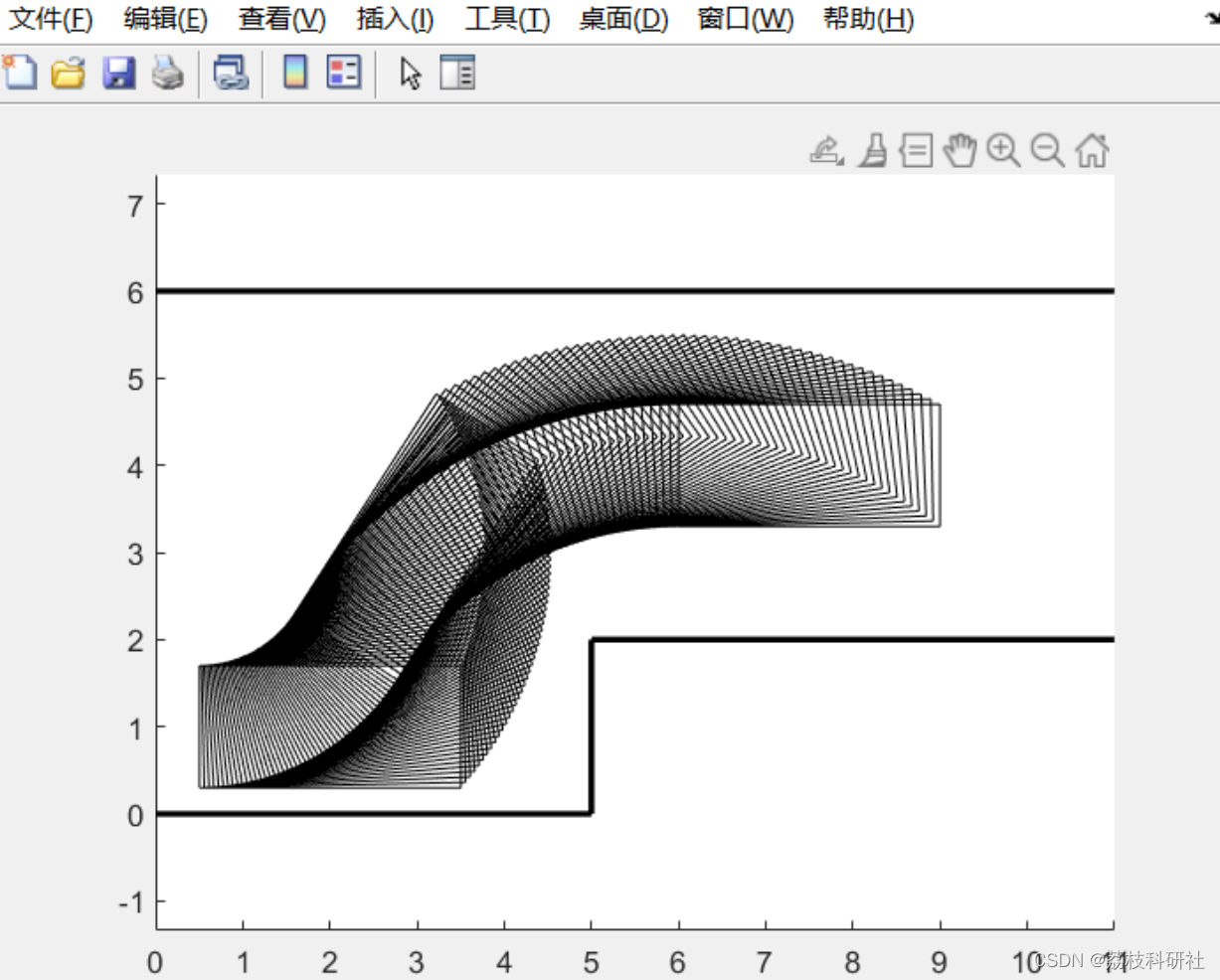
主函数部分代码：

clc;clear;close all
%   main_line.m
%   一个简单的脚本实现自动泊车的路径规划动态演示，并对泊车路线进行曲线拟合。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 参数设定
up_limit = 6;%上边界纵坐标
front_p = [5, 2]; % 车位信息C点, 参见说明文档最后碰撞检测第二部分
right_limit = 11; % 横坐标右边界

o_3 = [0.5, 1]; % 泊车点
ini = [6, 4];   % 初始点

c_l = 3; % 车长
c_w = 1.4; % 车宽
r_min = 2;    % 最小转弯半径
plot_vec = 0.01; % 动画速度, 数越小, 越快, 为0直接出图
fit_model = 0; % 拟合形式, 1位高次多项式, 其他数为傅里叶级数拟合, 图中最后出现的红色曲线为拟合曲线
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1)
hold on
grid on
%% 泊车区域限定
% 左下角坐标, 沿x长度, 沿y长度
line([0, right_limit],          [up_limit, up_limit]    ,'LineWidth',2, 'Color',[0 0 0]);
line([0, front_p(1)],           [0, 0]                  ,'LineWidth',2, 'Color',[0 0 0]);
line([front_p(1), front_p(1)],  [0, front_p(2)]         ,'LineWidth',2, 'Color',[0 0 0]);
line([front_p(1), right_limit], [front_p(2), front_p(2)],'LineWidth',2, 'Color',[0 0 0]);
axis([0 right_limit 0 up_limit], 'equal');
%% 参数
x = ini(1); y = ini(2); % 车辆后轴中心点坐标
c_o = [x, y];

c_line(1,:) = [x,       x,       y - c_w/2, y + c_w/2];
c_line(2,:) = [x,       x + c_l, y + c_w/2, y + c_w/2];
c_line(3,:) = [x + c_l, x + c_l, y + c_w/2, y - c_w/2];
c_line(4,:) = [x + c_l, x,       y - c_w/2, y - c_w/2];

for i = 1:4
    car(i) = line([c_line(i,1),c_line(i,2)], [c_line(i,3), c_line(i,4)],'LineWidth',1.5, 'Color',[0 0 0]);
end
%% 弧长确定
% 倒推法, 根据最小转弯半径确定弧2的圆心
cir2 = [o_3(1), o_3(2) + r_min];
% plot(cir2(1), cir2(2), 'ro');

% 根据过初始点和泊车点的圆的圆心确定最大半径
k_1 = (c_o(2) - o_3(2)) / (c_o(1) - o_3(1));
k_2 = - 1/k_1;
r_max = y - (k_2 * x + ((c_o(2) + o_3(2))/2 - k_2*(c_o(1) + o_3(1))/2)); % 第一次转弯最大半径

% 弧1, 根据最大最小转弯半径确定的圆心
p_rmin = [x, y - r_min];
p_rmax = [x, y - r_max];

% 最小转弯半径对应的到圆心2-r_min的距离和到初始点的距离, 以及所对应的转角
v_min = p_rmin - cir2;
l_min = norm(v_min) - r_min; % 最小转弯半径时, 与o_3连线得到的半径对比
d_min = y - p_rmin(2);
alpha_min = pi/2 - atan2(abs(v_min(2)), abs(v_min(1)));
% alpha_min*180/pi

% 最大转弯半径对应的到圆心2-r_min的距离和到初始点的距离, 以及所对应的转角
v_max = p_rmax - cir2;
l_max = norm(v_max) - r_min;
d_max = y - p_rmax(2);
alpha_max = pi/2 - atan2(abs(v_max(2)), abs(v_max(1)));
% alpha_max*180/pi

% 2分法找满足相切的两个弧的, 弧1的半径和圆心
l_middle = inf;
d_middle = 0;
% 由于弧1以最小转弯半径对应圆心构成的到初始点的长一般小于到圆心2的点, 同理, 另一个相反. 以此判断条件, 是否满足泊车最低要求.
if (l_min > d_min) && (l_max < d_max)
    while abs(l_middle - d_middle) > 0.000001
        % 根据中间角度对应的射线与x = x交点作为圆心, 计算l和d
        alpha_middle = (alpha_max + alpha_min)/2;
        k_middle = -tan(pi/2 - alpha_middle);
        y_middle = k_middle*c_o(1) + (cir2(2) - k_middle*cir2(1));
        d_middle = y - y_middle;
        v_middle = [x, y_middle] - cir2;
        l_middle = norm(v_middle) - r_min;
        
        if l_middle > d_middle
            v_min = [x, y_middle] - cir2;
            l_min = norm(v_min) - r_min; % 最小转弯半径时, 与o_3连线得到的半径对比
            d_min = y - y_middle;
            alpha_min = pi/2 - atan2(abs(v_min(2)), abs(v_min(1)));
        else
            v_max = [x, y_middle] - cir2;

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]李红. 自动泊车系统路径规划与跟踪控制研究[D].湖南大学,2014. 

 🌈4 Matlab代码实现