目录
前言
在《有限单元法》课程的学习中,对于杆系结构有限单元法的求解,笔者走了许多弯路,也产生了些许思考与浅薄的见解。结合个人经验与编程大作业,借助本帖来分享笔者的MATLAB编程求解思路,也希望与各位朋友友好讨论相关问题。
本文基于“先处理法”处理位移约束, 并秉持“面向对象程序设计语言的三大原则:封装、继承、多态”这一基本思想,给出MATLAB杆系结构通解程序,并分享所有源代码以交流讨论。
正文
1 例题
已知平面刚架单元的角度,长度和材料属性:EA=7.2e6kN,EI=2.16e5kNm2,求整体坐标系下的单元结点位移和约束反力。

2 分析
研究对象:钢架结构;
结点:刚节点(3自由度);
单元:梁单元。
3 求解
3.1 项目结构设计思路
基于“面向对象程序设计语言的三大原则:封装、继承、多态”这一基本思想,笔者将该项目程序分为“主程序”与“函数”,主程序只包含“求解对象基本信息的输入”与“函数的调用”,并无过多的复杂流程,这使得主程序结构清晰,可读性强,整体代码量较低。
项目整体使用先处理法处理位移约束。相较于后处理法,先处理法编程思路更加清晰,更易于变成,且总体刚度矩阵阶数更小。
3.2 主程序
借鉴工程问题有限单元法分析流程,笔者将主程序的功能设计为四部分:“基本信息的输入”、“前处理”、“分析”、“后处理”。
3.2.1 基本信息的输入
| 名称 | 符号 | 输入格式 | 功能 |
| 弹性模量 | EA | 7.2e6 | 输入单元弹性模量 |
| 抗弯刚度 | EI | 2.16e5 | 输入单元抗弯刚度 |
| 结点自由度 | nodof | 3 | 输入结点自由度数 |
| 结点坐标 | geom1 | [x1,y1;x2,y2;...] | 输入结点全局坐标 |
| 单元结点关联矩阵 | connec1 | [单元 i 结点1,单元 i 结点2;] | 输入单元内结点的关系 |
| 位移约束 | Constr | [节点号,x约束,y约束,转角约束] | 有约束为1,自由为0 |
| 力约束 | force_ele | 结点力输入: force_ele=[节点号,单元号,LoadNO,q,a1]; 结间力输入: force_ele=[ 0 ,单元号,LoadNO,q,a2]; | 按照格式输入,便于后续利用等效节点载荷处理。 【LoadNO:等效节点力标识;q:荷载大小;a1:结点到单元局部系原点距离;a2:作用范围】 |
| 缩放因子 | factor | 300 | 将变形放大300倍 |
3.2.2 前处理
对输入信息进行简单处理,为后续“分析”计算做准备。
1.钢架基本信息的运算
利用输入信息生成结点数nnd、单元节点数nne、单元自由度eldof等变量,减少信息的输入。
2.结点位移边条的处理
利用自定义的bound函数来处理位移约束,生成边条矩阵 nf 及活跃自由度数 nn。
3.等效结点载荷的处理
利用自定义的Force_equal函数来处理力约束,生成综合等效结点载荷矩阵loads_ele。
3.2.3 分析
1.总体刚度矩阵kk及总体力阵F的形成
利用自定义的FormKK函数来生成单元刚度矩阵kl(局部系)、kg(总体系)和单元力阵fl(局部系)、fg(总体系),并组装总体刚度矩阵kk与总体力列阵F。
2.总体平衡矩阵的求解
求解总体平衡矩阵得出结点位移delta。
总体平衡矩阵
即
3. 单元力&约束反力计算
利用自定义的ElemForce函数来生成单元力矩阵Force_all和约束反力矩阵R。
3.2.4 后处理
1.计算结果的输出
利用自定义的printresult函数将总刚kk、结点位移列阵delta、轴力&剪力&弯矩(包含在Force_all中)、反力R集中输出。
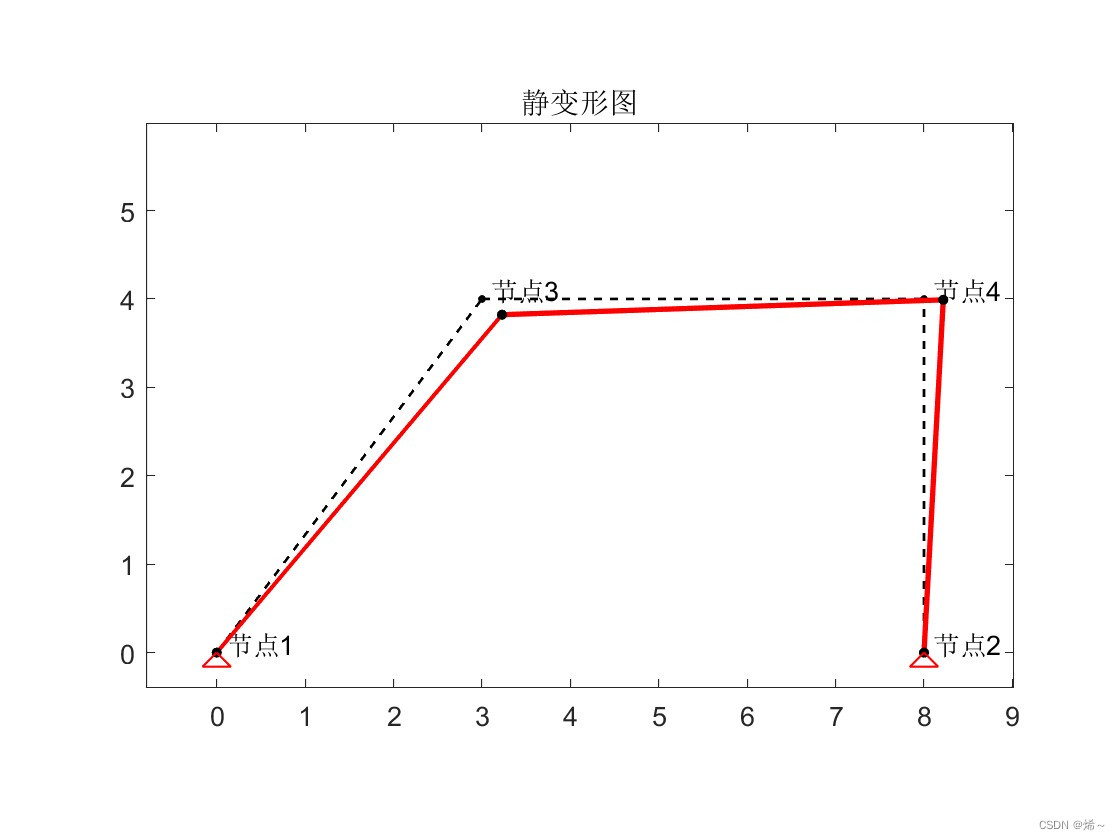
2.绘制静变形图
利用自定义的RenderFrame函数绘制静变形图。
%%主程序
%%先处理法求解钢架问题
%%作者:@烯~
%零、基本信息输入
format short e
EA = 7.2e6; EI = 2.16e5; % 材料属性
nodof = 3; % 节点自由度
geom1 = [0 0;8 0;3 4;8 4]; % 节点坐标
connec1 = [1 3;3 4;2 4]; % 单元节点关联矩阵
Constr = [1,0,0,0;2,0,0,0]; % 边条(位移约束)
force_ele = [3,2,1, 30,0; % 边条(力约束)
4,2,2, 30,5;
0,2,3,-18,5];
factor = 300; % 变形缩放系数
%一、前处理
%1 钢架基本信息运算
nnd = size(geom1,1); % 节点数
nne = size(connec1,2); % 单元节点数
eldof = nne*nodof; % 单元自由度
%2 节点位移边条的生成
[nf,n] = bound(Constr,nnd,nodof);
%3 等效节点荷载的生成
loads_ele = Force_equal(connec1,force_ele);
%二、分析
%1 总刚/总F的形成
[kk,F] = Formkk(EA,EI,geom1,connec1,loads_ele,nf,eldof,n,nodof);
%2 总体平衡矩阵的求解
delta = kk\F;
%3 单元力/约反力计算
[Force_all,R] = ElemForce(loads_ele,EA,EI,geom1,connec1,nf,eldof,delta,Constr);
%三、后处理
%1 计算结果的输出
printresult(kk,delta,Force_all,R);
%2 静变形图的绘制
RenderFrame(factor,nf,delta,nodof,connec1,geom1,Constr,2,'-r');3.3 函数
3.3.1 边界条件处理函数
function [nf,n]=bound(Constr,nnd,nodof)
% 本函数处理边界条件
% 作者:@烯~
%输入:Constr约束条件;nnd结点数;nodof节点自由度数
%输出:nf位移边界矩阵;n激活的自由度数
%1) 假设每个节点每个自由度都未被约束。
nf = ones(nnd,nodof); % 将nf初始化为 1
%2) 对实际有约束的自由度设置为0
for j=1:size(Constr,1)
nf(Constr(j),:)=0;
end
%3) 对未被约束的节点进行编号
n=0;
for i=1:nnd
for j=1:nodof
if nf(i,j) ~= 0
n=n+1; %n为激活的自由度数
nf(i,j)=n;
end
end
end
end3.3.2 等效结点力求解函数
本函数虽然只支持三种荷载类型的输入,单其结构完整且通用,可以很容易套用该模板来分丰富其功能,以便于求解更多在和类型。
function loads_ele= Force_equal(connec1,force_node)
% 本函数求解等效结点力
% 作者:@烯~
% 结点力输入:
% force_ele=[节点号,单元号,LoadNO,q,结点到单元局部系原点距离];
% 结间力输入:
% force_ele=[ 0 ,单元号,LoadNO,q,作用范围];
% LoadNO:等效节点力标识
% 【1:轴向结点集中力;2:结点/结间集中力偶;3:横向均布荷载;】
% q:荷载大小
%1 初始化荷载
nel = size(connec1,1); % 单元数
loads_ele=zeros(nel,6);
%2 将荷载分类组装
n1=0;n2=0;n3=0;
LoadNo=zeros(1,size(force_node,1));
for i=1:size(force_node,1)
LoadNo(i)=force_node(i,3);
switch LoadNo(i)
case 1
n1=n1+1;% 储存该类别等效节点力个数
elem1(n1)=force_node(i,2);% 储存单元位置
force1(n1,:)=force_node(i,:);
case 2
n2=n2+1;
elem2(n2)=force_node(i,2);
force2(n2,:)=force_node(i,:);
case 3
n3=n3+1;
elem3(n3)=force_node(i,2);
force3(n3,:)=force_node(i,:);
end
end
%3 计算等效节点力
%1) 组装轴向结点集中力
F1=zeros(nel,6); % 1类型单元等效结点力初始化
for i=1:n1
node=force1(i,1);
elemn=force1(i,2);
[~,b]=find(connec1(elemn,:)==node);% 搜寻结点在单元中的相对位置
if b==1
F1(elem1(i),1)=force1(i,4);
elseif b==2
F1(elem1(i),4)=force1(i,4);
end
end
%2) 组装结点集中力偶
F2=zeros(nel,6);
for i=1:n2
M=force2(i,4);
xi=force2(i,5);
a=force2(i,5);L=a;
F2(elem2(i),:)=M*[0 -6*xi/(L^2)+6*xi^2/(L^3) 1-4*xi/L+3*xi^2/(L^2) 0 6*xi/(L^2)-6*xi^2/(L^3) -2*xi/L+3*xi^2/(L^2)];
end
%3) 组装横向均布荷载
F3=zeros(nel,6);
syms x
for i=1:n3
q=force3(i,4);
a=force3(i,5);L=a;
N_v=[0 1-3*x^2/L^2+2*x^3/L^3 x-2*x^2/L+x^3/L^2 0 3*x^2/L^2-2*x^3/L^3 -x^2/L+x^3/L^2];
F3(elem3(i),:)=int(q*N_v,0,a);
end
%4 组装总等效单元荷载
for i=1:nel
loads_ele(i,:)=F1(i,:)+F2(i,:)+F3(i,:); % 单元总等效节点力
end
end3.3.3 总刚&总力求解函数
1.主函数
function [kk,F]=Formkk(EA,EI,geom1,connec1,loads_ele,nf,eldof,n,nodof)
% 本函数求解总刚kk和总力F
% 作者:@烯~
%1 初始化
F = frame_loads(n,nodof,nf);% 荷载初始化
nel = size(connec1,1); % 单元数
kk = zeros(n,n); % 总刚初始化
%组装总刚kk和总力F
for i=1:nel
[kg,T] = frame_kg(i,EA,EI,geom1,connec1);% 求整体系下单刚kg和坐标变换阵T
disp(['单刚(整体系) kg ',num2str(i),'=']);disp(kg);
fl=loads_ele(i,:);
fg=T*fl';
g = frame_g(i,connec1,nf); % 求解单元操作矢量
kk = form_KK(kk,kg,g,eldof); % 组装总刚
F = frame_loads_ele(F,fg,g,eldof); % 计算结果同PPT
end
end2.子函数1:求解单刚
function [kg,T] = frame_kg(i,EA,EI,geom,connec)
% 本函数形成整体系下的单刚【钢架】
% 作者:@烯~
% 输入:i第i个单元;EA刚度;geom节点坐标;connec单元节点关联矩阵
% 输出:kg单刚,T坐标变换阵
ndim = size(geom,2); % ndim为计算问题的维数
node_1=connec(i,1);node_2=connec(i,2);
switch ndim
case 1
x1=geom(node_1);
x2=geom(node_2);
L=abs(x1-x2);
kl=EI/(L^3)*[ 12 6*L -12 6*L;
6*L 4*L*L -6*L 2*L*L;
-12 -6*L 12 -6*L;
6*L 2*L*L -6*L 4*L*L ];
kg=kl;
case 2
x1=geom(node_1,1); y1=geom(node_1,2);
x2=geom(node_2,1); y2=geom(node_2,2);
L = sqrt((x2-x1)^2 + (y2-y1)^2);
kl=[ EA/L 0 0 -EA/L 0 0;
0 12*EI/L^3 6*EI/L^2 0 -12*EI/L^3 6*EI/L^2;
0 6*EI/L^2 4*EI/L 0 -6*EI/L^2 2*EI/L ;
-EA/L 0 0 EA/L 0 0;
0 -12*EI/L^3 -6*EI/L^2 0 12*EI/L^3 -6*EI/L^2;
0 6*EI/L^2 2*EI/L 0 -6*EI/L^2 4*EI/L ];
C=(x2-x1)/L; S=(y2-y1)/L;
T=[C S 0 0 0 0;
-S C 0 0 0 0;
0 0 1 0 0 0;
0 0 0 C S 0;
0 0 0 -S C 0;
0 0 0 0 0 1];
kg=T'*kl*T;
end
end3.子函数2:总刚组装函数
function kk = form_KK(kk,kg,g,eldof)
% 本函数组装总刚(先处理法)【桁架,钢架】
% 作者@烯~
for i=1:eldof
if g(i) ~= 0
for j=1: eldof
if g(j) ~= 0
kk(g(i),g(j))= kk(g(i),g(j))+kg(i,j);
end
end
end
end
end4.子函数3:操纵矢量组装函数
function g = frame_g(i,connec,nf)
% @烯~
% 本函数形成操作矢量【钢架】
%操作矢量确定了单刚哪个位置需组装至总刚(由节点边条确定);操作矢量中不为0的位置需要组装至总刚.
%1.对于任意i单元,检索其关联关系矩阵connec(,)的第1个节点和第2个节点
node1=connec(i,1);
node2=connec(i,2);
%2.从元素的自由度形成操作矢量
g=[nf(node1,1);
nf(node1,2);
nf(node1,3);
nf(node2,1);
nf(node2,2);
nf(node2,3)];
end5.子函数4:结点载荷生成函数
function F = frame_loads(n,nodof,nf)
% 本函数形成结点载荷
% @烯~
nnd = size(nf,1); % 节点数
F= zeros(n,1);
loads = zeros(nnd,3); % 所有节点载荷初始化为0
for i=1:nnd
for j=1:nodof
if nf(i,j)~= 0
F(nf(i,j)) = loads(i,j);
end
end
end
end6.子函数5:单元载荷生成函数
function F = frame_loads_ele(F,fg,g,eldof)
% 本函数形成单元载荷
% @烯~
for idof=1:eldof
if (g(idof))~= 0
F(g(idof))= F(g(idof))+ fg(idof);
end
end
end3.3.4 单元力&约束反力计算函数
function [Force_all,R]=ElemForce(loads_ele,EA,EI,geom1,connec1,nf,eldof,delta,Constr)
% 本函数求解轴力,剪力,弯矩,反力
% @烯~
%1 求单元内力
nel = size(connec1,1); % 单元数
edg=zeros(1,eldof); % 单元位移初始化
force_g=zeros(eldof,nel);force_l=zeros(eldof,nel); % 未消去等效节点力的总体系/局部系下的力
Force_g=zeros(eldof,nel);Force_l=zeros(eldof,nel); % 已消去等效节点力的总体系/局部系下的力
for i=1:nel
[kg,T] = frame_kg(i,EA,EI,geom1,connec1);
g = frame_g(i,connec1,nf);
for j=1:eldof
if g(j)== 0
edg(j)=0.; % 被约束的自由度位移为0
else
edg(j) = delta(g(j));
end
end
force_g(:,i) = kg*edg';
force_l(:,i) = T'*force_g(:,i) ;
f0=loads_ele(i,:); % 单元等效节点力
Force_l(:,i)=force_l(:,i)-f0';
Force_g(:,i)=T*Force_l(:,i);
end
%2 求解轴力、剪力、弯矩
Force_FL=Force_l([1,4],:); % 轴力
Force_FQ=Force_l([2,5],:); % 剪力
Force_M=Force_l([3,6],:); % 弯矩
Force_all={Force_FL,Force_FQ,Force_M};% 储存轴力、剪力、弯矩
%3 提取反力
R=zeros(size(Constr,1),3);%初始化反力
for i=1:size(Constr,1)
[b,a]=find(connec1==Constr(i,1));%寻找结点在单元的位置(b=单元1结点;a=单元2结点)
R(i,:)=[abs(Force_FL(a,b)),abs(Force_FQ(a,b)),abs(Force_M(a,b))];
end
end3.3.5 结果输出函数
function printresult(kk,delta,Force_all,R)
% 本函数输出计算结果
% @烯~
disp('总刚为 kk = ');disp(kk);
disp('结点位移为:');disp(delta);
Force_FL=Force_all{1,1};
Force_FQ=Force_all{1,2};
Force_M=Force_all{1,3};
disp('轴力为:');disp(' 单元1 单元2 单元3');disp(Force_FL);
disp('剪力为:');disp(' 单元1 单元2 单元3');disp(Force_FQ);
disp('弯矩为:');disp(' 单元1 单元2 单元3');disp(Force_M);
disp('约束反力为:');disp(' 轴力 剪力 弯矩 ');disp(R);
end3.3.6 变形图绘制函数
function RenderFrame(factor,nf,delta,nodof,connec,geom,Constr,LineWidth,LineStyle)
% 本函数绘制桁架变形图
% @烯~
%1 求结点位移
nnd = size(geom,1); % 节点数
nel = size(connec,1); % 单元数
node_disp=zeros(nnd,nodof);
for i=1:nnd
for j=1:nodof
node_disp(i,j)=0;
if nf(i,j)~=0
node_disp(i,j)=delta(nf(i,j));
end
end
end
%2 求静变形后的坐标
geom2=zeros(nnd,2);
for i=1:2*nnd
geom2(i)=geom(i)+node_disp(i)*factor;
end
%3 绘图
figure('Name','静变形图','NumberTitle','off');
CoordScale=[max(geom(:,1))-min(geom(:,1)),max(geom(:,2))-min(geom(:,2))];
%1) 绘制结点
for i=1:nnd
plot(geom(i,1),geom(i,2),'.','MarkerSize',10, ...
'MarkerFaceColor','k','MarkerEdgeColor','k')
a1=num2str(i);
a2=['节点',a1];
text(geom(i,1)+0.1,geom(i,2)+0.1,a2)
hold on
end
for i=1:nel
line([geom(connec(i,1),1),geom(connec(i,2),1)], ...
[geom(connec(i,1),2),geom(connec(i,2),2)],'Color', ...
'k','LineStyle','--','LineWidth',1);
end
%2) 绘制杆件
for i=1:length(connec(:,1))
plot([geom2(connec(i,1),1),geom2(connec(i,2),1)], ...
[geom2(connec(i,1),2),geom2(connec(i,2),2)],...
LineStyle,'LineWidth',LineWidth*connec(i,2)/max(connec(:,2)));
hold on
end
%3) 绘制变形后节点
for i=1:length(geom2(:,1))
x1=geom2(i,1);y1=geom2(i,2);
scatter(x1,y1,15,'k','filled')
end
%4) 绘制约束--选用结构最大的坐标尺寸作为基准来绘制约束
for i=1:length(Constr(:,1))
plot([geom2(Constr(i,1),1) geom2(Constr(i,1),1)- ...
0.02*max(CoordScale) geom2(Constr(i,1),1)+...
0.02*max(CoordScale) geom2(Constr(i,1),1)], ...
[geom2(Constr(i,1),2) geom2(Constr(i,1),2)-...
0.02*max(CoordScale) geom2(Constr(i,1),2)- ...
0.02*max(CoordScale) geom2(Constr(i,1),2)],...
'LineWidth',0.8,'color','r');
end
%5) 绘制坐标轴
axis equal
title('静变形图')
axis([min(geom2(:,1))-0.1*CoordScale(1),max(geom2(:,1))+ ...
0.1*CoordScale(1),min(geom2(:,2))-...
0.1*CoordScale(2),max(geom2(:,2))+0.5*CoordScale(2)]) %限定图像的显示范围
hold off
end3.4 结果展示
单刚(整体系) kg 1=
5.3167e+05 6.8125e+05 -4.1472e+04 -5.3167e+05 -6.8125e+05 -4.1472e+04
6.8125e+05 9.2906e+05 3.1104e+04 -6.8125e+05 -9.2906e+05 3.1104e+04
-4.1472e+04 3.1104e+04 1.7280e+05 4.1472e+04 -3.1104e+04 8.6400e+04
-5.3167e+05 -6.8125e+05 4.1472e+04 5.3167e+05 6.8125e+05 4.1472e+04
-6.8125e+05 -9.2906e+05 -3.1104e+04 6.8125e+05 9.2906e+05 -3.1104e+04
-4.1472e+04 3.1104e+04 8.6400e+04 4.1472e+04 -3.1104e+04 1.7280e+05
单刚(整体系) kg 2=
1440000 0 0 -1440000 0 0
0 20736 51840 0 -20736 51840
0 51840 172800 0 -51840 86400
-1440000 0 0 1440000 0 0
0 -20736 -51840 0 20736 -51840
0 51840 86400 0 -51840 172800
单刚(整体系) kg 3=
40500 0 -81000 -40500 0 -81000
0 1800000 0 0 -1800000 0
-81000 0 216000 81000 0 108000
-40500 0 81000 40500 0 81000
0 -1800000 0 0 1800000 0
-81000 0 108000 81000 0 216000
总刚为 kk =
1.9717e+06 6.8125e+05 4.1472e+04 -1.4400e+06 0 0
6.8125e+05 9.4980e+05 2.0736e+04 0 -2.0736e+04 5.1840e+04
4.1472e+04 2.0736e+04 3.4560e+05 0 -5.1840e+04 8.6400e+04
-1.4400e+06 0 0 1.4805e+06 0 8.1000e+04
0 -2.0736e+04 -5.1840e+04 0 1.8207e+06 -5.1840e+04
0 5.1840e+04 8.6400e+04 8.1000e+04 -5.1840e+04 3.8880e+05
结点位移为:
7.5554e-04
-5.9332e-04
-2.0410e-04
7.2710e-04
-3.3236e-05
1.4217e-04
轴力为:
单元1 单元2 单元3
-1.7563e+01 1.0963e+01 -5.9825e+01
1.7563e+01 -4.0963e+01 5.9825e+01
剪力为:
单元1 单元2 单元3
2.6876e+01 3.0175e+01 -4.0963e+01
-2.6876e+01 5.9825e+01 4.0963e+01
弯矩为:
单元1 单元2 单元3
3.2154e+01 -1.4520e+01 7.4249e+01
1.4520e+01 -8.9603e+01 8.9603e+01
约束反力为:
轴力 剪力 弯矩
1.7563e+01 2.6876e+01 3.2154e+01
5.9825e+01 4.0963e+01 7.4249e+01
4 讨论
本项目是在学习《有限单元法》这一本科课程的产物,该项目是第三个版本,我见证了这个项目从“不同教材的拼接”,到“蕴含个人思考”的转变;从原本的“手算流程的机械化复现”,到现在的“面向对象、化繁为简”,不禁唏嘘不已。该项目仍有许多不足之处,比如“等效结点载荷的求解”需要完善、“后处理”可以添加“弯矩图、剪力图、轴力图的绘制”,使功能更加丰富。后续在学有余力的情况下,会进一步完善该项目,并进行分享。
5 参考资料
[1]丁星, 王清远. MATLAB杆系结构分析[M]. 科学出版社, 2008.
[2]崔济东,沈雪龙.有限单元法——编程与软件应用[M]. 中国建筑工业出版社,2019.
[3]江文强.MATLAB和Abaqus有限元分析理论与应用[M]. 中国工信出版集团,2020.
后记
这是笔者第一次在网络上公开发文,笔者只是一名普通的本科生,在学习中经常碰壁,经常走弯路。然而,诸如CSDN、知乎、BIlibili等平台的博主们无私地提供了许多优质学习资源与宝贵的个人经验,使我收获颇多,也使我想向这些千千万万的博主们一样,分享我个人在学习生活中的见解和经验,希望能将经验分享,能将知识传递,能将这份理念传递。希望我的文章能帮助与我一样有这类困扰的朋友,也希望能在求学之路上结交到更多志同道合的伙伴。
后续,我也经秉持着“开放、共享、传递”这一理念,分享我在“力学”、“有限单元法”、“MATLAB编程”、“MATLAB AppDesigner程序开发”等方面的所思所感,希望各位朋友多多包容与支持,十分感谢。
























 439
439

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








