目录
算法学习
算法原理
迪杰斯特拉(Dijkstra)算法是用于解决只有非负权值的图的单源最短路径问题的算法。
迪杰斯特拉本质是一种局部贪心的思路,算法过程如下:
1 将图中所有的节点分为两个集合,S和Q,S为以确定最短路径的节点的集合,而Q为未确定最短路径的节点的集合。
在初始条件下,只有起点是确定最短路径的,为0,所以初始条件 S中只有起点,其他的节点都在Q中,后续每确定起点到一个节点的最短路径,就会将对应节点从Q中移除,加入到S中。
2 每一次从 Q 中找一个起点到该节点代价最小(路径最短,权值最小)的节点u。
每一轮我们都能确定一个点,起点到该点的最短路径能够确定。
3 将u从Q中移除,加入到S,然后对u的每一个相邻节点进行松弛操作。
松弛操作我们可以简单理解为:尝试从已确定最短路的节点前往所有的邻节点,看是否能够得到更小的路径。对于未确定最短路径的所有节点,从起点有一条或者多条路径能够到达该店,所以从起点到达该点的路径有多种值。 我们每有一个确定最短路径的节点,会尝试从这个点去到达所有未确定最短路径的邻节点,如果从本点到邻节点的路径比当前记录的路径要小,我们可以更新邻节点的路径为从起点到本节点,再从本节点到邻节点。
这样文字讲述起来其实并不好理解,我们可以用示例来分析,假设我们有这样一个图:

图为有向图,起点为0节点,我们需要求出从起点到达其他四个节点的最短路径。
我们需要一个dis数组来保存起点到所有结点的最短路径,在Dijkstra过程中可能保存的是当前所记录的最短路径。 dis[i] 表示从起点到节点 i 的最短路径。
首先集合 S 中只有一个节点 S{0},其中dis[0] = 0;然后我们需要从0节点对他的所有邻节点进行松弛操作,于是 dis数组就更新为了: dis = [0,5,7,13,11 ];

下一步从Q中选取一个路径最短的节点,本轮选取的节点为节点1,因为dis[1] < dis[2] < dis[4] < dis[3]。 那么我们本轮就能确定从起点到节点1的最短路径就是当前dis数组中记录的最短路径。
为什么呢? 因为图中所有的边的权值都非负,而从起点到节点1如果有很多的走法,不管从哪一条路径走,都会首先经过至少一个中间点,假设中间点为 x ,因为 dis{0->1}的路径已经是所有的dis中最小的了,那么到达中间点x的路径为 dis[x] ,本身 dis[1] <= dis[x],而从中间点x到节点1还至少需要走一条边,假设边的权值为 y ,而y >= 0 ,那么从中间节点x到节点1的路径就为 dis[x] + y,而 dis[1] <= dis[x] + y,说明直接从起点走到节点1的路径,一定是小于等于从其他的中间节点走到节点1的,那么最坏情况下,dis[1] == dis[x] + y ,此时我们的 dis[1] 仍然是最短路径。 这其实是一种局部贪心的策略。
那么我们将节点1从Q加入到S之后,还需要对节点1的邻节点进行松弛操作。

那么在本轮结束之后,我们就能够确定0和1的最短路径,下一步就继续从Q中选取一个最短路径的节点,本轮取出的节点为节点 2 , 因为 dis[2] < dis[4] < dis[3]; 所以当前的 dis[2] 就是从起点到节点2的最短路径,理由如上。因为当前已经确定最短路径的节点只有0和1,那么我们需要判断从节点0或者节点1到达Q中的点的所有路径中,最小的路径,而我们初始情况下dis数组中记录的就是从节点0到达所有节点的路径,而在第一轮取出节点1的时候,又更新了dis数组,dis数组中当前保存的是 从节点0直接到该点的路径 以及 从节点0先沿最短路径到达节点1,再从节点1到达目标点,这两种路径中的较小路径。那么Q中未确定最短路径的节点中,最小的路径为节点2的路径,这已经是 dis[2] = min {dis{0->2} , dis{0->1->2}},也就是min{dis{0->x->2}} x为S中的节点,到达节点2还可能有其他的路径,也就是先从0到达Q的节点,再去往节点2,但是由于当前所记录的 dis 中,从起点到达Q中所有的节点的路径都大于等于 dis[2] ,那么从起点到达这些节点本身路径就大于等于dis[2]了,再加上从该点到达节点2,路径只会更大,所以dis[2]已经是最优解了。

然后我们再对2的邻节点进行松弛操作。

那么以此类推,下一个从Q中取出或者说能够确定最短路径的节点就是节点 4 ,节点4取出来之后,松弛操作之后的 dis = [0,5,7,11,9]
最后再取出节点 3,松弛操作之后,dis = [0,5,7,11,9]。
那么这样一来,所有的节点都已经确定了最短路径,而最短路径就保存在dis数组中。
在Dijkstra的过程中,可能在某一轮的时候,有些节点还没有任何路径能够到达,比如下面的这个图:

在初始情况下,并没有从节点0到达节点4的边,那么起始的 dis[4]其实是未定义的,或者没有路径到达,那么如何定义呢? 由于后续我们需要从dis数组中取出一个未确定最短路径的最小值,也就是取min,那么为了让这些点不影响这个过程,我们需要将其初始化为正无穷大 0x3f3f3f3f。
还有就是如果最终图中的某些节点根本无法到达,也就是某一轮选出的最小的 dis = 0x3f3f3f3f,说明这些节点无法从起点到达, 那么我们可以提前结束Dijkstra的过程。
以上是使用单向图来举例,双向图的Dijkstra也是一样的思路。
#include<iostream>
#include<vector>
using namespace std;
vector<int> Dijkstra(int n, const vector<vector<int>>& grid, int k) {
}
int main() {
int n = 5; //节点个数
vector<vector<int>> grid{ {0,1,5},{0,2,7},{0,3,13},{0,4,11},{1,3,6},{1,4,4},{2,3,7},{2,4,3} }; //边,每一个grid[i]也就是 [x,y,z] 表示的是从x到y有一条边,权值为z
int k = 0; //起点
vector<int> dis = Dijkstra(n, grid, k);
return 0;
}根据图和边的比例,或者说稠密图和稀疏图,有两种做法,当然思路是一样的,只是代码形式有所不同。
稠密图Dijkstra模板

对于稠密图,也就是几乎所有的两个节点之间都有边,那么此时使用邻接矩阵来存储边的关系更加适合。
邻接矩阵 g[i][j] ,表示的是从节点 i 到节点 j 之间有一条边,权值为 g[i][j] ,当然也可能不存在,我们可以定义 i 到 j 没有直接边相连时,g[i][j] = -1;
如果是双向图,对于[i,j,z]表示的是i到j和j到i都有一条边,权值都为z,那么从事 g[i][j] = g[j][i] =z;
那么第一步就是创建一个邻接矩阵:
vector<vector<int>> g(n, vector<int>(n, -1));
for (auto& v : grid) g[v[0]][v[1]] = v[2];第二步就是创建一个dis数组,用于记录最短路径, 还需要一个数组 S ,s[i]用于记录节点是否已确定最短路径,并对起点进行初始化;
const int INF = 0x3f3f3f3f;
vector<int> dis(n, INF); //记录路径
vector<bool> S(n, false); //记录节点是否已确定最短路径
//初始化
dis[k] = 0; 注意在这里我们并没有对 S[k] 进行初始化,这样一来可以在循环的过程中对起点k的所有邻节点进行松弛操作,节省了我们对 k 的邻节点初始化的工作量。
//稠密图Dijkstra
vector<int> Dijkstra(int n, const vector<vector<int>>& grid, int k) {
//初始化邻接矩阵
vector<vector<int>> g(n, vector<int>(n, -1));
for (auto& v : grid) g[v[0]][v[1]] = v[2];
const int INF = 0x3f3f3f3f;
vector<int> dis(n, INF); //记录路径
vector<bool> S(n, false); //记录节点是否已确定最短路径
//初始化
dis[k] = 0;
//取最短路径并进行松弛操作
while (1) {
//首先需要找到一个未确定最短路径的节点中的最短路径
int x = -1 , mindis = INF;
for(int i = 0 ; i < n ; ++i){
if (!S[i] && dis[i] < mindis) { //注意这里是 dis[i] < mindis
x = i, mindis = dis[i];
}
}
if (x == -1) break; //此时有两种情况:1、所有节点的最短路径都已确定; 2、有节点不可达,此时也不需要继续进行松弛
//然后对 i 的邻节点进行松弛操作
S[x] = true;
for (int j = 0; j < n; ++j) {
if (!S[j] && g[x][j] != -1 && mindis + g[x][j] < dis[j]) { //三个条件:Q中的节点,x->j有边, dis[k->x->j] < dis[j]
dis[j] = mindis + g[x][j];
}
}
}
return dis;
}
稀疏图Dijkstra模板
对于稠密图,由于边的数量很多很多,那么在遍历 g[i][j]的时候,大多数都是有效遍历,也就是g[i][j] > -1,但是对于稀疏图,也就是边的数量远小于点的数量的平方,那么此时如果使用邻接矩阵的话,就会导致大部分的位置上都是-1,空间浪费过大,同时在遍历g[i][j]的时候,大多数都是无效遍历,所以稀疏图不适合采用邻接矩阵来存储边,而采用邻接表。
邻接表其实也很简单,我们也可以用二维数组来存储,只不过不是直接开 n* n的空间,而是根据具体的边的数量来开辟空间。
邻接表可以使用 vector<vector<pair<int,int>>> 来存储
对于g[i] ,是一个一维数组,每一个元素是pair<int,int>,其中 first 存储的是节点的编号,int存储的是边的权值, g[i][j] 表示的是从节点 i 到节点 g[i][j].first 存在一条边,边的权值为 g[i][j].second。
那么我们可以这样初始化邻接表:
vector<vector<pair<int, int>>> g;//邻接矩阵
for (auto& v : grid) g[v[0]].emplace_back(v[1], v[2]);同时,对于算法的过程,我们也可以优化。
由于我们会多次求dis中最小的路径,那么我们其实可以将未确定的节点在dis中记录的路径放到一个最小堆中,后续我们直接去堆顶的元素,就能拿到最短路径。
我们使用这样一个堆来存储:
class mygreater {
public:
bool operator()(const pair<int, int>& p1, const pair<int, int>& p2) { return p1.second > p2.second; }
};
priority_queue<pair<int, int>, vector<pair<int, int>>, mygreater> pq; //first存节点的编号,second存路径但是这样有一个问题:
按照上面的流程,我们在第一轮循环中,会将1~4节点都入堆,此时堆中有节点1,2,3,4的路径

在第二轮循环中,我们会取出节点1,并对节点1的邻节点进行松弛操作,那么此时如果发现对应的dis需要更新,那么就需要对该节点以及更新后的路径再次入堆,也就是会对3和4再次入堆。

那么此时堆中就有两个节点3和4的路径信息,那么两次出堆都需要更新最短路径以及松弛操作吗?
很简单,对于堆中同一个节点的多个路径,我们只会用到最小的,同时,该节点的最短路径一定是第一个出堆的该节点的pair,当第一个该节点的键值对出堆的时候,最短路径就确定了,此时dis数组中记录的就是这个最短路径,那么需要进行松弛操作,后续再次出堆,此时的 second 保存的路径一定大于 dis 中的路径,那么此时就不再需要进行松弛操作。
在使用堆来优化的情况下,既提高了找最小值的效率,也节省了S数组的空间。
代码如下:
//稀疏图Dijkstra
vector<int> Dijkstra(int n, const vector<vector<int>>& grid, int k) {
vector<vector<pair<int, int>>> g(n);//邻接矩阵
for (auto& v : grid) g[v[0]].emplace_back(v[1], v[2]); //first存储边的目的节点,second存储边的权值
const int INF = 0x3f3f3f3f;
vector<int>dis(n, INF);
class mygreater {
public:
bool operator()(const pair<int, int>& p1, const pair<int, int>& p2) { return p1.second > p2.second; }
};
priority_queue<pair<int, int>, vector<pair<int, int>>, mygreater> pq; //first存节点的编号,second存路径
//首先将起点入堆
dis[k] = 0;
pq.emplace(0, 0);
while (!pq.empty()) {
auto p = pq.top();
pq.pop();
if (dis[p.first] > p.second) continue; //非第一次出堆
//走到这里说明 dis[p.firrst] == p.second
//那么说明是对应节点的路径信息第一次出堆,本次出堆的一定是最小路径,那么需要进行松弛操作
int mindis = p.second, x = p.first;
//松弛操作
for (auto& pj : g[x]) //对x的出边遍历
{
if (mindis + pj.second < dis[pj.first]) //说明从k 到 x 再到 j 的路径小于当前dis数组记录的 k到j的路径,那么需要更新
{
dis[pj.first] = mindis + pj.second;
//入堆
pq.emplace(pj.first, dis[pj.first]);
}
}
}
//走到这里堆为空,如果有不可到达的节点,那么dis数组不会发生任何更新,保存的还是 INF
return dis;
}练习
1 网络延迟时间


题目解析:题目给我们所有的边,节点总数,以及起点,要我们求起点传播到其他点的最远时间,如果有节点无法到达,返回-1,如果所有点都可到达,那么需要返回最远的点的最短路径。
本题就是一个标准的Dijkstra问题,需要求出起点到所有点最短路径,在算法题中,我们一般就认为是稀疏图,一般都是使用邻接表来存储边,而Dijkstra的过程其实就和我们的模板一样。
但是要注意的一点就是一般题目中给的节点编号是从1开始,而不是0开始。
代码如下:
class Solution {
public:
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const pair<int,int>&p1,const pair<int,int>&p2){return p1.second > p2.second;}
};
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<vector<pair<int,int>>> g(n+1); //g[i] 存储节点i的边
for(auto&v:times) g[v[0]].emplace_back(v[1],v[2]);
vector<int> dis (n+1 , INF);
priority_queue<pair<int,int>,vector<pair<int,int>>,mygreater> pq;
dis[k] = 0;
pq.emplace(k,0);
while(!pq.empty()){
auto p = pq.top();
pq.pop();
if(p.second > dis[p.first]) continue; //不是第一次出堆
int x = p.first , mindis = p.second;
//松弛操作
for(auto& py : g[x]){
if(mindis + py.second < dis[py.first]){ //更新
dis[py.first] = mindis + py.second;
pq.emplace(py.first,dis[py.first]);
}
}
}
int res = -INF;
for(int i = 1 ; i <= n ; ++i){
res = max(res , dis[i]);
}
return res == INF ? -1 : res;
}
};
2 到达最后一个房间的最少时间Ⅰ


题目解析:一共有 n*m 个房间,每个房间有一个最小开启时间,也就是在这个时间之前,无法向该房间移动,比如times[1][1]=3,那么在第3s之前无法向{1,1}移动。 每一次移动只能移动到相邻的房间,也就是上下左右四个房间,相邻房间的移动需要耗时一秒,返回到达{m-1.n-1}房间的最少时间。
题目隐含的信息其实有两个:
1、每一个节点有四条边,与其上下左右四个节点直接相连。
2、每一条边的权值为1。
但是本题在求最短路径的时候有一个限制,假设我们更新了 {i,j} 的最短时间dis[i][j],那么更新dis[i+1][j]的时候,除了要考虑dis[i][j] 的大小之外,还需要考虑能够前往{i+1,j}的最短时间,也就是moveTime[i+1][j] ,最早在这个时间才能开始向{i+1,j}开始移动,而移动需要耗时1s,那么到达{i+1,j}房间的最早时间就是 moveTime[i+1][j]+1,所以如果我们使用 dis[i][j] + 1 算出来的时间比 moveTime[i+1][j]+1小,那么此时最早到达时间是 moveTime[i+1][j] + 1;
还有就是由于这里的节点是一个二元组,那么我们就需要保存二元组的位置以及路径,那么我们可以直接使用一个vector来入堆,后续出堆的时候就能很快提取位置和路径。
其他的地方没有需要修改的。
class Solution {
public:
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<int>&v1,const vector<int>&v2){return v1[2] > v2[2];}
};
int minTimeToReach(vector<vector<int>>& moveTime) {
int m = moveTime.size() , n = moveTime[0].size();
vector<vector<int>> dis(m,vector<int>(n,INF));
//起点为 0,0
dis[0][0] = 0;
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
pq.push({0,0,0});
while(!pq.empty()){
//取出堆顶元素
auto v = pq.top();
pq.pop();
//判断是不是最短路径第一次出栈
if(v[2] >dis[v[0]][v[1]]) continue;
int x = v[0] , y = v[1] , mindis = v[2];
if(x > 0 && (dis[x-1][y] == INF || max(mindis , moveTime[x-1][y]) + 1 < dis[x-1][y])){ //更新(x-1,y)
dis[x-1][y] = max(mindis , moveTime[x-1][y]) + 1;
pq.push({x-1,y,dis[x-1][y]});
}
if(y > 0 && (dis[x][y-1] == INF || max(mindis , moveTime[x][y-1]) + 1 < dis[x][y-1])){ //更新(x,y-1)
dis[x][y-1] = max(mindis , moveTime[x][y-1]) + 1;
pq.push({x,y-1,dis[x][y-1]});
}
if(x + 1 < m && (dis[x+1][y] == INF || max(mindis,moveTime[x+1][y]) + 1 < dis[x+1][y])){//更新(x+1,y)
dis[x+1][y] = max(mindis,moveTime[x+1][y]) + 1;
pq.push({x+1,y,dis[x+1][y]});
}
if(y + 1 < n && (dis[x][y+1] == INF || max(mindis,moveTime[x][y+1]) + 1 < dis[x][y+1])){//更新(x,y+1)
dis[x][y+1] = max(mindis,moveTime[x][y+1]) + 1;
pq.push({x,y+1,dis[x][y+1]});
}
}
return dis[m-1][n-1];
}
};
同时,在这种只需要求一个点的最短路径的情况下,其实是完全有可能提前求出来的,也就是说,我们并不需要求出所有的点的dis,而是只需要目标点,那么在出堆的过程中,如果目标点第一次出堆,一定是最短路径,此时我们就可以直接返回了,这也算是一个小优化。
class Solution {
public:
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<int>&v1,const vector<int>&v2){return v1[2] > v2[2];}
};
int minTimeToReach(vector<vector<int>>& moveTime) {
int m = moveTime.size() , n = moveTime[0].size();
vector<vector<int>> dis(m,vector<int>(n,INF));
//起点为 0,0
dis[0][0] = 0;
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
pq.push({0,0,0});
while(!pq.empty()){
//取出堆顶元素
auto v = pq.top();
pq.pop();
//判断是不是最短路径第一次出栈
if(v[2] >dis[v[0]][v[1]]) continue;
int x = v[0] , y = v[1] , mindis = v[2];
if(x == m-1 && y == n-1) return mindis; //提前结束
if(x > 0 && (dis[x-1][y] == INF || max(mindis , moveTime[x-1][y]) + 1 < dis[x-1][y])){ //更新(x-1,y)
dis[x-1][y] = max(mindis , moveTime[x-1][y]) + 1;
pq.push({x-1,y,dis[x-1][y]});
}
if(y > 0 && (dis[x][y-1] == INF || max(mindis , moveTime[x][y-1]) + 1 < dis[x][y-1])){ //更新(x,y-1)
dis[x][y-1] = max(mindis , moveTime[x][y-1]) + 1;
pq.push({x,y-1,dis[x][y-1]});
}
if(x + 1 < m && (dis[x+1][y] == INF || max(mindis,moveTime[x+1][y]) + 1 < dis[x+1][y])){//更新(x+1,y)
dis[x+1][y] = max(mindis,moveTime[x+1][y]) + 1;
pq.push({x+1,y,dis[x+1][y]});
}
if(y + 1 < n && (dis[x][y+1] == INF || max(mindis,moveTime[x][y+1]) + 1 < dis[x][y+1])){//更新(x,y+1)
dis[x][y+1] = max(mindis,moveTime[x][y+1]) + 1;
pq.push({x,y+1,dis[x][y+1]});
}
}
return dis[m-1][n-1];
}
};
3 到达最后一个房间的最少时间Ⅱ


解析题目:本题与上一题是一个类型的题目,也有可以前往对应房间的最早时间的限制,但是本题还多出了一个限制,就是如果是第奇数次移动,那么本次移动需要1秒,如果是第偶数次移动,那么本次移动需要2秒。
其实暴力的方法很简单,我们再入堆的时候,直接再添加一个元素,就是下一次移动是第几次,那么后续我们进行松弛操作的时候就能知道下一次移动需要1秒还是2秒。代码如下:
class Solution {
public:
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<int>&v1,const vector<int>&v2){return v1[3] > v2[3] ; }
};
int minTimeToReach(vector<vector<int>>& moveTime) {
int m = moveTime.size(), n = moveTime[0].size();
vector<vector<int>> dis(m,vector<int>(n,INF));
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
dis[0][0] = 0;
pq.push({0,0,1,0}); //v[0]表示横坐标,v[1]表示纵坐标,v[2]表示下一次移动是第几次移动,v[3]表示路径长度
while(!pq.empty()){
auto v = pq.top();
pq.pop();
int x = v[0] , y = v[1] , cnt = v[2] , mindis = v[3] , t = 2 - cnt % 2; //t表示松弛操作的时间,也就是下一次移动所需要的时间
if(mindis > dis[x][y]) continue;
if(x == m - 1 && y == n - 1) return mindis;
if(x > 0 && (dis[x-1][y] == INF || max(mindis , moveTime[x-1][y]) + t < dis[x-1][y])){ //更新(x-1,y)
dis[x-1][y] = max(mindis , moveTime[x-1][y]) + t;
pq.push({x-1,y,cnt+1,dis[x-1][y]});
}
if(y > 0 && (dis[x][y-1] == INF || max(mindis , moveTime[x][y-1]) + t < dis[x][y-1])){ //更新(x,y-1)
dis[x][y-1] = max(mindis , moveTime[x][y-1]) + t;
pq.push({x,y-1,cnt+1,dis[x][y-1]});
}
if(x + 1 < m && (dis[x+1][y] == INF || max(mindis , moveTime[x+1][y]) + t < dis[x+1][y])){ //更新(x+1,y)
dis[x+1][y] = max(mindis , moveTime[x+1][y]) + t;
pq.push({x+1,y,cnt+1,dis[x+1][y]});
}
if(y + 1 < n && (dis[x][y+1] == INF || max(mindis , moveTime[x][y+1]) + t < dis[x][y+1])){ //更新(x,y+1)
dis[x][y+1] = max(mindis , moveTime[x][y+1]) + t;
pq.push({x,y+1,cnt+1,dis[x][y+1]});
}
}
return dis[m-1][n-1];
}
};
本题还有一种更巧妙的做法,其实对于这种网格图,我们从当前位置的坐标,就能知道下一次移动是奇数次还是偶数次移动。
我们的起点是 (0,0) ,两个坐标都是偶数,那么横纵坐标之和也是偶数,下一次移动就是第一次移动。移动的时候,是将横坐标加以或者减一 或者 纵坐标加一或者减一,那么不管怎么说,都会导致其中一个坐标变成奇数,那么横纵坐标值和就变成了奇数。
而对于(0,1),两个坐标之和为奇数,下一次移动一定是第偶数次移动,因为只有经历奇数次移动才会使横纵坐标之和为奇数。
那么我们就能够根据当前所处的房间的下标(x,y)推导出下一次移动是第奇数次移动还是第偶数次移动,如果x+y是奇数,那么下一次就是第偶数次移动,如果x+y是偶数,那么下一次就是第奇数次移动。
代码如下:
class Solution {
public:
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<int>&v1,const vector<int>&v2){return v1[2] > v2[2] ; }
};
int minTimeToReach(vector<vector<int>>& moveTime) {
int m = moveTime.size(), n = moveTime[0].size();
vector<vector<int>> dis(m,vector<int>(n,INF));
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
dis[0][0] = 0;
pq.push({0,0,0}); //v[0]表示横坐标,v[1]表示纵坐标,v[2]表示下一次移动是第几次移动,v[3]表示路径长度
while(!pq.empty()){
auto v = pq.top();
pq.pop();
int x = v[0] , y = v[1] , mindis = v[2] , t = 1 + (x + y) % 2; //t表示松弛操作的时间,也就是下一次移动所需要的时间
if(mindis > dis[x][y]) continue;
if(x == m - 1 && y == n - 1) return mindis;
if(x > 0 && (dis[x-1][y] == INF || max(mindis , moveTime[x-1][y]) + t < dis[x-1][y])){ //更新(x-1,y)
dis[x-1][y] = max(mindis , moveTime[x-1][y]) + t;
pq.push({x-1,y,dis[x-1][y]});
}
if(y > 0 && (dis[x][y-1] == INF || max(mindis , moveTime[x][y-1]) + t < dis[x][y-1])){ //更新(x,y-1)
dis[x][y-1] = max(mindis , moveTime[x][y-1]) + t;
pq.push({x,y-1,dis[x][y-1]});
}
if(x + 1 < m && (dis[x+1][y] == INF || max(mindis , moveTime[x+1][y]) + t < dis[x+1][y])){ //更新(x+1,y)
dis[x+1][y] = max(mindis , moveTime[x+1][y]) + t;
pq.push({x+1,y,dis[x+1][y]});
}
if(y + 1 < n && (dis[x][y+1] == INF || max(mindis , moveTime[x][y+1]) + t < dis[x][y+1])){ //更新(x,y+1)
dis[x][y+1] = max(mindis , moveTime[x][y+1]) + t;
pq.push({x,y+1,dis[x][y+1]});
}
}
return dis[m-1][n-1];
}
};
4 访问消失节点的最少时间



解析题目:给定图的边,同时给定每个节点的消失时间,当到达时间大于等于节点的消失时间的时候,那么该节点无法到达。
本题相较于直接求最短路径多出了一个限制条件,也就是每个节点有一个消失的时间,我们只有在消失时间之前到达该节点才是有效的。
那么就有两种情况:
1、到达节点i的最短路径 dis[i] < disqppear[i] ,那么此时节点 i 是可到达的,需要进行松弛操作。
2、到达节点的最短路径 dis[i] >= disappear[i],那么此时节点i是不可达的,那么自然也无法通过该节点去往其他节点,那么不需要进行松弛操作,同时需要将dis[i] 置为-1,表示不可达。
其他的思路则还是和单源最短路径一样。
代码如下:
class Solution {
class mygreater{
public:
bool operator()(const vector<int>&v1,const vector<int>&v2){return v1[1] > v2[1];}
};
const int INF = 0x3f3f3f3f;
public:
vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {
vector<int> dis(n,INF);
vector<vector<pair<int,int>>> g(n); //邻接表
for(auto& v: edges){
g[v[0]].push_back(make_pair(v[1],v[2]));
g[v[1]].push_back(make_pair(v[0],v[2])); //注意题目的图是双向图
}
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
pq.push({0,0});
dis[0] = 0;
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[1] > dis[v[0]]) continue; //如果v[0]最短路已经不可达了,那么此时dis[v[0]] == -1,走当前if出去了
else if(v[1] >= disappear[v[0]]){ //走到这里说明本轮出堆的已经是最短路,最早到达时间
dis[v[0]] = -1; //说明最早到达时间节点已经消失,那么无法到达
continue;
}
else{ //v[0]节点消失之前可到达,那么需要松弛操作
for(auto&p : g[v[0]]){ //g[v[0]]的邻边
if(dis[p.first] == INF||p.second + v[1] < dis[p.first]){
dis[p.first] = v[1] + p.second; //在这里先不判断 v1[1] + p.second < disappear[i],出堆再判断
pq.push({p.first,dis[p.first]});
}
}
}
}
//再将不可达的点标记出来
for(auto& e:dis) if(e == INF) e=-1;
return dis;
}
};
5 设计可以求最短路径的图类


解析题目:题目要求我们设计一个类,构造函数初始化节点的个数,初始边的情况。然后还需要实现两个函数,一个用于添加有向边,一个用于求两个节点的最短路径。那么其实很简单,我们可以使用邻接表来保存边的集合,而求最短路径的时候,由于题目给出了边的权值是大于1的,所以我么可以直接使用Dijkstra算法来求。虽然题目还提示了调用函数的次数,但是Dijkstra算法的时间复杂度并不高,相当于 O(M+N),M为点的数量,N为边的数量,所以还是能够解决的。
那么代码如下:
class Graph {
public:
class mygreater{
public:
bool operator()(const vector<int>&v1,const vector<int>&v2){return v1[1] > v2[1];}
};
Graph(int n, vector<vector<int>>& edges)
:_n(n),_g(n)
{
for(auto& v : edges)_g[v[0]].push_back(make_pair(v[1],v[2]));
}
void addEdge(vector<int> edge) {
_g[edge[0]].push_back(make_pair(edge[1],edge[2]));
}
int shortestPath(int node1, int node2) {
vector<int> dis(_n,INF);
dis[node1] = 0;
_pq.push({node1,0});
while(!_pq.empty()){
auto v = _pq.top();
_pq.pop();
if(dis[v[0]] < v[1]) continue;
for(auto& p : _g[v[0]]){
if(p.second + v[1] < dis[p.first]){
dis[p.first] = v[1] + p.second;
_pq.push({p.first,dis[p.first]});
}
}
}
while(!_pq.empty()) _pq.pop();
return dis[node2] == INF ? -1 : dis[node2];
}
private:
const int INF = 0x3f3f3f3f;
int _n;
vector<vector<pair<int,int>>> _g;
priority_queue<vector<int>,vector<vector<int>>,mygreater>_pq;
};
6 概率最大的路径


解析题目:题目给定一些边,同时每一条边都只有 succProb[i] 的概率能够通过,要求我们求出从起点到重点的所有路径中,通过概率最大的路径的概率。 对于一条路径的通过概率,等于他的所有的边的概率的乘积。
那么初看这个题好像是求最大的概率,那么好像并不是求最小路经,但是我们可以借鉴Dijkstra的思想。
题目给定所有的概率succProb[i] <= 1 ,那么其实如果从起点开始,走向起点的邻边,那么会有一条通过概率最大的边,那么从起点通过改变到达该点,就是从起点到该点的最大概率路径,因为所有的边的概率都小于等于1,如果从其他的路径走,最终到达该点的也不会超过这个概率,那么我们其实可以使用一个最大堆来模拟这个过程,松弛操作的时候也不再是加法,而是乘法,只有大于当前所记录的概率的时候才会更新。
代码如下:
class Solution {
public:
class myless{
public:
bool operator()(const pair<int,double>&p1 , const pair<int,double>&p2){return p1.second < p2.second;}
};
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start_node, int end_node) {
vector<double> dis(n,2.0); //我们使用一个大于1的概率作为默认值,表示不可达
vector<vector<pair<int,double>>> g(n);
for(int i = 0 ; i < edges.size() ; ++i){
g[edges[i][0]].push_back(make_pair(edges[i][1],succProb[i]));
g[edges[i][1]].push_back(make_pair(edges[i][0],succProb[i]));
}
priority_queue<pair<int,double>,vector<pair<int,double>>,myless> pq;
dis[start_node] = 1.0;
pq.push(make_pair(start_node,1.0));
while(!pq.empty()){
auto p = pq.top();
if(p.first == end_node) return p.second;
pq.pop();
if(p.second < dis[p.first]) continue; //不是通往该点的最大概率
//是通往该点的最大概率,那么需要松弛操作
for(auto& p1 : g[p.first]){//对 p.first 的邻点 p1 进行松弛操作
if(dis[p1.first] > 1.0 || p.second * p1.second > dis[p1.first]){ //发现更大概率的路径
dis[p1.first] = p.second * p1.second;
pq.push(make_pair(p1.first,dis[p1.first]));
}
}
}
return 0;
}
};
7 最小体力消耗路径



题目解析:本题是一个求最短路径的题目,但是本题对于路径的定义不是路径上所有边的权值之和,而是所有的边的权值的最大值,所以我们在更新路径的时候换一种更新方式就行了。本题与到达最后一个房间的最少时间是同一类问题,二维空间的移动。
代码如下:
class Solution {
public:
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>& v2){return v1[2] > v2[2];}
};
const int INF = 0x3f3f3f3f;
int minimumEffortPath(vector<vector<int>>& heights) {
int m = heights.size() , n = heights[0].size();
vector<vector<int>> dis(m,vector<int>(n,INF));
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
dis[0][0] = 0;
pq.push({0,0,0});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[2] > dis[v[0]][v[1]]) continue; //不是第一次出堆
//第一次出堆,更新 (v[0],v[1]) 的最短路径,进行松弛操作
int x = v[0] , y = v[1] , mindis = v[2];
if(x == m-1 && y == n-1) return mindis;
if(x > 0 && (dis[x-1][y] == INF || dis[x-1][y] > max(mindis , abs(heights[x][y] - heights[x-1][y])))){ //更新 dis[x-1][y]
dis[x-1][y] = max(mindis,abs(heights[x][y] - heights[x-1][y]));
pq.push({x-1,y,dis[x-1][y]});
}
if(y > 0 && (dis[x][y-1] == INF || dis[x][y-1] > max(mindis , abs(heights[x][y] - heights[x][y-1])))){ //更新 dis[x][y-1]
dis[x][y-1] = max(mindis,abs(heights[x][y] - heights[x][y-1]));
pq.push({x,y-1,dis[x][y-1]});
}
if(x + 1 < m && (dis[x+1][y] == INF || dis[x+1][y] > max(mindis , abs(heights[x][y] - heights[x+1][y])))){ //更新 dis[x+1][y]
dis[x+1][y] = max(mindis,abs(heights[x][y] - heights[x+1][y]));
pq.push({x+1,y,dis[x+1][y]});
}
if(y + 1 < n && (dis[x][y+1] == INF || dis[x][y+1] > max(mindis , abs(heights[x][y] - heights[x][y+1])))){ //更新 dis[x][y]
dis[x][y+1] = max(mindis,abs(heights[x][y] - heights[x][y+1]));
pq.push({x,y+1,dis[x][y+1]});
}
}
return dis[m-1][n-1];
}
};
8 从第一个节点出发到最后一个节点的受限路径数



题目解析:本题给定n个节点,编号从1开始,要求我们求出从1到n的受限路径的数量。
受限路径的定义:对于一条路径,有多个节点以及相邻节点连接的边构成,假设节点序列为 (1,N2,N3...Nk,Nk+1...n),那么这些节点必须要满足一个特性,我们需要知道从节点 n 到其中每一个节点Ni的最短路径 dis[i] ,那么需要满足 : dis[1] > dis[N2] > dis[N3] > dis[N4] > ... >dis[Nk] > dis[Nk+1]...>dis[n],也就是每个节点到n的最短路径都需要比路径中下一个节点到节点n的最短路径长。
那么不管怎么说,我们都需要先求出从节点n到其他所有结点的最短路径dis[i],这一步我们可以使用Dijkstra来完成。
class Solution {
public:
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>&v2){return v1[1] > v2[1];}
};
const int INF = 0x3f3f3f3f;
int countRestrictedPaths(int n, vector<vector<int>>& edges) {
vector<int> dis(n+1,INF);
vector<vector<vector<int>>> gout(n+1); //出边邻接表,用于计算最短路径
vector<vector<int>> gin(n+1); //入边邻接表,只需要保存边,不需要保存边的权重
for(auto&v:edges){
gout[v[0]].push_back({v[1],v[2]});
gout[v[1]].push_back({v[0],v[2]});
gin[v[0]].push_back(v[1]); //v[0]有一条入边,起点为v[1]
gin[v[1]].push)back(v[0]); //v[1]有一条出边,起点为v[0]
}
//Dijkstra求最短路径
dis[n] = 0;
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
pq.push({n,0});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[1] > dis[v[0]]) continue;
for(auto& v1 : g[v[0]]){
if(dis[v1[0]] == INF || dis[v1[0]] > v1[1] + v[1]){
dis[v1[0]] = v1[1] + v[1];
pq.push({v1[0],dis[v1[0]]});
}
}
}
//走到这里就把从节点n到所有的点的最短路径求出来保存在了 dis[i]中
}
};那么接下来我们就需要求出从节点 1 到节点 n 的受限路径的个数,由于从节点1到节点n有很多的路径可以到达,我们可以将这些路径拆分为两部分,先从节点 1 到节点 X,需要满足节点1到节点 X有一条边,同时 dis[1] > dis[X] ,然后另一部分就是从节点X到达节点n的一条受限路径,那么我们的问题就转换为了求节点X到节点n的受限路径的个数。
那么我们可以使用动态规划来解决这个问题:
dp[i] 表示从节点 i 到节点 n 的受限路径的数量
状态转移方程推导:
对于dp[i],从节点i到节点n的受限路径的数量,我们需要拆分成两部分,首先从节点i到达节点X,要求这条路径是受限路径,也就是 dis[i] > dis[X] ,然后再从X到节点n,这一条路径也必须是受限路径,那么从i到X再到n的受限路径的个数就是 dp[X]。
但是可能有多个X满足从i到X是受限路径,从X到n有受限路径,那么我们需要保证在填写dp[i]的时候,所有的满足条件的dp[X]都需要已经填完。这时候我们就可以思考一下,由于X必须要满足dis[X] < dis[i],那么意味着当填到 dp[i] 的时候,所有的dis[X]<dis[i] 的位置都需要已经填完,那么我们的填表顺序就是按照 dis[i] 的大小,从小到大填表。
为了保证这个填表顺序,我们可以使用一个堆来保存 dis[i] 和 i ,然后依次取出对堆顶元素,按照dis[i]的从小到大填写 dp[i]。
细节问题:
初始化:需要初始化 dp[n] = 1
填表顺序:按照dis[i]的从小到大,依次填写 dp[i]
返回值:dp[1]
代码如下:
class Solution {
public:
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>&v2){return v1[1] > v2[1];}
};
const int INF = 0x3f3f3f3f;
const int MOD = 1e9+7;
int countRestrictedPaths(int n, vector<vector<int>>& edges) {
vector<int> dis(n+1,INF);
vector<vector<vector<int>>> gout(n+1); //出边邻接表
for(auto&v:edges){
gout[v[0]].push_back({v[1],v[2]});
gout[v[1]].push_back({v[0],v[2]});
}
//Dijkstra求最短路径
dis[n] = 0;
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
pq.push({n,0});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[1] > dis[v[0]]) continue;
for(auto& v1 : gout[v[0]]){
if(dis[v1[0]] == INF || dis[v1[0]] > v1[1] + v[1]){
dis[v1[0]] = v1[1] + v[1];
pq.push({v1[0],dis[v1[0]]});
}
}
}
//走到这里就把从节点n到所有的点的最短路径求出来保存在了 dis[i]中
vector<long long> dp(n+1 , 0) ; //dp[i]表示从节点i到节点n的受限路径数量
dp[n] = 1; //
//按照 dis[i] 的升序来填写dp[i]
for(int i = 1 ; i < n ; ++i){
pq.push({i,dis[i]});
}
while(!pq.empty()){
auto v = pq.top();
pq.pop();
int i = v[0];
//填写dp[i],看i有多少出边,以及与出边是否满足受限路径
for(auto& v1: gout[i]){
if(dis[i] > dis[v1[0]]) dp[i] = (dp[i] + dp[v1[0]]) % MOD;
}
if(i == 1) break;
}
return dp[1];
}
};
9 最短路径中的边


解析题目:题目给定m条边,我们需要求出节点0到节点n-1的所有最短路径中所用到过的边,返回一个数组用于表示edges中的那那些边被用到了,哪些没被用到。
判断每一条边是否为某个点最短路径的一条边,我们需要在Dijkstra的过程中进行操作。对于每一个节点的最短路径,比如dis[i] ,我们可以分成两部分来看,最短路径中最后一条边为 j -> i ,那么最短路径其实就是从起点到j的最短路径,然后再加上 j->i 这一条边,就组成了从起点到节点i的最短路径。
我们可以理解为:从起点到任意一个节点 i 的最短路径,一定是从起点到某一个节j点的最短路径,再加上节点 j 到节点 i 的边。
那么我们是不是可以理解为: 每新增一个节点,那么最短路径的边就会多出一条。
那么对于每个节点的最短路径,我们是不是可以额外保存一个东西,就是他的最短路径中的最后一条边,这样一来,我们在计算完所有的节点的最短路径之后,就能知道所有的最短路径的最后一条边,也就是所有的组成最短路径的边,只有这些边是在最短路径中的,其他的边都不在最短路径中。
那么我们在Dijkstra的过程中,更新的dis[i]的时候,还需要更新dis[i]的最后一条边,我们可以使用一个数组 vector<vector<int>> use 来记录,use[i] 存储的是dis[i]的最后一条边在 edges 的下标,因为可能存在多条最短路径,所以可能有多条边需要存储。
那么use数组就能保存所有点的最短路径的最后一条边。
但是题目要求的是从节点0到节点n-1的所有最短路径中的所有边,那么n-1的所有最短路径,不管怎么样,都可以拆分为前一个点到n-1的边以及前一个点的最短边。
可能多条最短路径,那么n-1的前一个点可能是一个,也可能有多个都可以通过最短路径到n-1,那么我们只需要记录一下上一个点。
那么我们在使用一个数组vector<vector<int>> prev , prev[i] 是一个一维数组,用于保存从起点的节点i的所有最短路径中,倒数第二个节点编号。
那么后续我们就能够根据 prev[n-1] 来到倒退出所有最短路径所经过的所有的节点,而到这些节点所需要的边能够在use数组中找到,那么就能够完成本题。
当然其实还可以继续优化,因为use数组和prev数组在功能上有重复,其实最终可以删除其中一个数组,但是其实思路不会有太大变化,所以我们这里也不进行优化了。
代码如下:
class Solution {
public:
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>&v2){return v1[1] > v2[1];}
};
const int INF = 0x3f3f3f3f;
void dfs(const vector<vector<int>>&prev,int end , unordered_set<int>&nodes){
if(nodes.find(end) != nodes.end()) return;
nodes.insert(end);
cout<<"dfs:end="<<end<<endl;
for(auto e : prev[end]){
if(nodes.find(e) != nodes.end())continue;
dfs(prev,e,nodes);
}
}
vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
vector<int> dis(n,INF);
vector<vector<int>> prev(n); //记录每个节点的所有最短路径的倒数第二个节点
vector<vector<vector<int>>> g(n); //g[i] 保存的是从节点i的出边,是一个一维数组vector,{x,y,z} x是目的节点,y是边的权值,z是边在edges的下标
for(int i = 0 ; i < edges.size() ; ++i){
g[edges[i][0]].push_back({edges[i][1],edges[i][2],i});
g[edges[i][1]].push_back({edges[i][0],edges[i][2],i});
}
vector<vector<int>> use(n); //use[i] 存储 dis[i] 的下标,有的dis[i] 不可达或者用不上,那么use[i] = -1,最后一条边也有可能有多个
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
dis[0] = 0 ;
pq.push({0,0});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[0] == n - 1) break; //后续所有的最短路径都大于等于 dis[n-1],就算能到n-1,也不是最短路径了
if(v[1] > dis[v[0]]) continue; //非最短路径出堆
//对 v[0] 的邻点进行松弛操作
for(auto& v1 : g[v[0]]){
if(dis[v1[0]] == INF || dis[v1[0]] > v[1] + v1[1]){ //找到更小路径,那么之前记录的prev[v1[0]]无效了
dis[v1[0]] = v[1] + v1[1];
use[v1[0]].clear();
use[v1[0]].push_back(v1[2]);
prev[v1[0]].clear();
prev[v1[0]].push_back(v[0]); //本条最短路径的倒数第二个节点为 v[0]
pq.push({v1[0],dis[v1[0]]});
}
else if(dis[v1[0]] == v[1] + v1[1]) {
prev[v1[0]].push_back(v[0]);
use[v1[0]].push_back(v1[2]);
}
}
}
//然后我们需要求出所有最短路径所经过的节点
//为了去重,我么可以使用 unordered_set 来存储
cout<<"---"<<endl;
for(auto e : prev[n-1]) cout<<e<<endl;
unordered_set<int> nodes;
//对于 prev[n-1],可能有多个节点的最短路径加上该节点到n-1的边是相等的最短路径,所以我们需要遍历
//由于需要大量的循环来判断,我们直接用递归来解决
dfs(prev,n-1,nodes);
vector<bool> ans(edges.size(),false);
for(auto e : nodes){ //用到的所有节点
for(auto i : use[e]){
ans[i] = true;
}
}
return ans;
}
};
10 到达目的地的方案数


解析题目:本题要求我们求出从节点0到节点n-1的最短路径的条数,这个题其实相对于上一个题比较简单,因为上一个题我们需要统计所有的最短路径的所有的节点,而这个题中我们只需要统计最短路径的条数。
类似的,假设其中有一条从0到n-1的最短路径的倒数第二个节点为 X ,而从X到n-1只有一条路,这一条路径长度是固定的,那么这条最短路径其实就是先从节点 0 到节点X的最短路径,再加上这一条边,那么就构成了从0到n-1的最短路径,那么经过X的最短路径有多少条,就取决于从0到n-1的最短路径有多少条。
那么这样一来,我们在更新每一个节点的最短路径dis[i]的时候,不仅需要记录最短路径的数值,还需要记录最短路径出现的次数,需要使用一个cnt数组来记录。
当我们使用其他节点对节点 i 进行松弛操作的时候,如果更新出了最短路径, mindis + g(x->i) < dis[i],那么此时是一条全新的最短路径,需要更新cnt[i] = cnt[x] ; 如果mindis + g(x->i) == dis[i] ,那么说明这一条路径也是从0到节点 i 的最短路径,那么需要对 cnt[i] += cnt[x];
最终当0到节点 n-1 的最短路径出堆的时候,我们就确定了一共有多少条最短路径,cnt[n-1],因为最短路径的确定其实在出堆之前就已经统计完了,不管是 dis[n-1] 还是 cnt[n-1]。
那么代码如下:
class Solution {
public:
const int MOD = 1e9+7;
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<long long>& v1 , const vector<long long>& v2){
return v1[1] > v2[1];
}
};
int countPaths(int n, vector<vector<int>>& roads) {
vector<long long> dis(n,INF);
vector<vector<vector<int>>>g(n);
for(auto&v:roads){
g[v[0]].push_back({v[1],v[2]});
g[v[1]].push_back({v[0],v[2]});
}
vector<long long>cnt(n,0);
priority_queue<vector<long long>,vector<vector<long long>>,mygreater> pq;
dis[0] = 0;
cnt[0] = 1;
pq.push({0,0});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[1] > dis[v[0]]) continue;
if(v[0] == n-1) break;
for(auto& v1 : g[v[0]]){
if(dis[v1[0]] == INF || dis[v1[0]] > v[1] + v1[1]){
dis[v1[0]] = v[1] + v1[1];
cnt[v1[0]] = cnt[v[0]];
pq.push({v1[0],dis[v1[0]]});
}
else if(dis[v1[0]] == v[1] + v1[1]) cnt[v1[0]] = (cnt[v1[0]] + cnt[v[0]])%MOD;
}
}
return cnt[n-1];
}
};
11 水位上升的泳池中游泳


题目解析:本题其实类似于到达最后一个房间的最少时间,每个方格都有最早可到达时间的限制,只有时间大于等于平台高度时才能到达本方格。
转换一下问题:我们需要找到一条路径,路径所经过的所有方格中,最大的方格的高度就是本条路径所需要的时间。那么我们需要找到一条节点数值最小的路径。
我们假设从节点 0 走到节点 x 所需的最少时间是 t1 ,t1其实就是代表从 0 到 x 的最短耗时路径中,高度最大的方格的高度,那么从 x 再走到 y ,如果y的高度是 t2 ,那么从 0 到 x 的所需要的时间就是 min(t1,t2)。
代码如下:
class Solution {
public:
const int INF = 0X3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>& v2){return v1[2] > v2[2];}
};
int swimInWater(vector<vector<int>>& grid) {
int n = grid.size();
vector<vector<int>> dis(n,vector<int>(n,INF));
dis[0][0] = grid[0][0];
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
pq.push({0,0,dis[0][0]});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[2] > dis[v[0]][v[1]]) continue;
if(v[0] == v[1] && v[1] == n - 1) return v[2];
//松弛操作,更新隔壁四个点最少时间
int x = v[0] , y = v[1] , mindis = v[2];
if(x > 0 && (dis[x-1][y] == INF || dis[x-1][y] > max(mindis , grid[x-1][y]))){
dis[x-1][y] = max(mindis , grid[x-1][y]);
pq.push({x-1,y,dis[x-1][y]});
}
if(y > 0 && (dis[x][y-1] == INF || dis[x][y-1] > max(mindis , grid[x][y-1]))){
dis[x][y-1] = max(mindis , grid[x][y-1]);
pq.push({x,y-1,dis[x][y-1]});
}
if(x + 1 < n && (dis[x+1][y] == INF || dis[x+1][y] > max(mindis , grid[x+1][y]))){
dis[x+1][y] = max(mindis , grid[x+1][y]);
pq.push({x+1,y,dis[x+1][y]});
}
if(y + 1 < n && (dis[x][y+1] == INF || dis[x][y+1] > max(mindis , grid[x][y+1]))){
dis[x][y+1] = max(mindis , grid[x][y+1]);
pq.push({x,y+1,dis[x][y+1]});
}
}
return dis[n-1][n-1];
}
};
12 前往目标的最小代价


解析题目:本题提供了两种路径,一种是直接从 {x1,y1} 走到 {x1,y2},此时需要的代价是 |x1-x2| + |y1-y1| ,另一种是通过页数路径,也就是题目给定的路径来走,代价则是指定的代价。
由于第一种走法会导致从一个点可以直接走到地图中的任意一个点,这样就会导致我们难以枚举这些路径,或者说枚举这些路径的复杂度过大,每一个点的路径就相当于有 m*n 条。但是其实第一种走法是可以转换一下:
每一次只走一格,也就是上下左右四个方向中选一个走,代价为1,满足 |x1-x2| + |y1-y2|,而从本节点到任意节点的直接的走法,其实可以看成是一步一步走过去的,每一次就走一格,那么本题的走法我们就可以替换一下:
1、走到上下左右四个邻格,代价为1
2、特殊路径,起点终点以及代价由题目指定。
那么接下来就是一个简单的Dijkstra的过程了。
但是我么可以注意一下题目的范围 : 起点和终点的横纵坐标范围 10^5 ,也就是十万,如果暴力Dijkstra的话,极有可能会超时,以及空间会溢出,那么我们不能直接进行暴力的dijkstra求解最短路径。
其实我们并不需要用到这么多的点,因为哪些没有特殊路径的点我们只能通过第一种方法到达,并不需要关注具体的最短路径,我们需要额外关注的是地图中的特殊路径,这样一来,我们其实可以首先将特殊路径的所有节点看成是一个图的节点,也就是一个建图过程。图中所有的节点都是相互连通的,可以通过第一种方法到达。
那么建图如何表示这些坐标呢?
由于所有的二维空间的坐标二元组都是 {x(int),y(int)},横纵坐标都是32位的,那么我们是不是可以直接用一个64位的整数来表示一个这样的二元组,我们使用 long long index = x << 32 + y ,来标识二维空间中的 {x,y} ,这个过程是可逆的,我们可以通过 64 位的一维位置逆转乘二元组。
我们可以为每一个节点进行编号,从0开始到n,使用数组来保存节点编号与其位置的关系,这一步需要使用哈希表去重。我们是在遍历特殊路径的时候来为节点编号的,在遍历的时候可以将邻接表也填好。
建图:无非就是为所有的边的两端节点进行编号,为了去重,我们需要使用一个哈希表来保存节点位置和节点编号的映射关系。
int minimumCost(vector<int>& start, vector<int>& target, vector<vector<int>>& specialRoads) {
int x = specialRoads.size() * 2 + 2; //最多x个节点
vector<long long> nodes(x);
unordered_map<long long , int> hash; //对节点进行去重
vector<vector<vector<int>>> g(x); //邻接表
int n = 1; //记录节点总数
nodes[0] = ((long long)start[0] << 32) + start[1]; //起点编号为 0
hash[nodes[0]] = 0; //保存0节点
for(auto& v : specialRoads){
long long x1 = v[0] , y1 = v[1] , x2 = v[2] , y2 = v[3] ;
int w = v[4];
long long n1 = (x1<<32) + y1 , n2 = (x2 << 32) + y2;
//判断两个节点是否已经存在,找节点编号
int index1 = 0 , index2 = 0;
if(hash.find(n1) == hash.end()){
hash[n1] = n;
nodes[n] = n1;
index1 = n++;
}
else index1 = hash[n1];
if(hash.find(n2) == hash.end()){
hash[n2] = n;
nodes[n] = n2;
index2 = n++;
}
else index2 = hash[n2];
//两个节点编号分别为 index1 和 index2
//维护邻接表
g[index1].push_back({index2,w});
// g[index2].push_back({index1,w}); //注意边是单向边
}
//n为节点总数
//然后还需要将终点记录
long long end = ((long long)target[0] << 32) + target[1];
if(hash.find(end) == hash.end()){
nodes[n] = end;
hash[end] = n;
n++;
}
int targetnode = hash[end]; //记录终点的节点编号,便于提前返回然后就是使用Dijkstra算法求最短路径,但是注意我们的终点的编号不一定是n-1,所以我们需要保存终点的节点编号。
Dijkstra的过程和我们的模板大差不差,只不过除了我们所记录的边之外,所有的节点两两之间都可以看作还有一条边,就是移动方法1的边,这些边我们也需要进行松弛操作。
全部代码如下:
class Solution {
public:
const int INF = 0x3f3f3f3f;
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>& v2){return v1[1] > v2[1];}
};
int getdistance(long long n1 , long long n2){
int x1 = n1>>32 , y1 = n1 & 0xffffffff , x2 = n2>>32 , y2 = n2 & 0xffffffff;
return abs(x1-x2) + abs(y1-y2);
}
int minimumCost(vector<int>& start, vector<int>& target, vector<vector<int>>& specialRoads) {
int x = specialRoads.size() * 2 + 2; //最多x个节点
vector<long long> nodes(x);
unordered_map<long long , int> hash; //对节点进行去重
vector<vector<vector<int>>> g(x); //邻接表
int n = 1; //记录节点总数
nodes[0] = ((long long)start[0] << 32) + start[1]; //起点编号为 0
hash[nodes[0]] = 0; //保存0节点
for(auto& v : specialRoads){
long long x1 = v[0] , y1 = v[1] , x2 = v[2] , y2 = v[3] ;
int w = v[4];
long long n1 = (x1<<32) + y1 , n2 = (x2 << 32) + y2;
//判断两个节点是否已经存在,找节点编号
int index1 = 0 , index2 = 0;
if(hash.find(n1) == hash.end()){
hash[n1] = n;
nodes[n] = n1;
index1 = n++;
}
else index1 = hash[n1];
if(hash.find(n2) == hash.end()){
hash[n2] = n;
nodes[n] = n2;
index2 = n++;
}
else index2 = hash[n2];
//两个节点编号分别为 index1 和 index2
//维护邻接表
g[index1].push_back({index2,w});
// g[index2].push_back({index1,w}); //注意边是单向边
}
//n为节点总数
//然后还需要将终点记录
long long end = ((long long)target[0] << 32) + target[1];
if(hash.find(end) == hash.end()){
nodes[n] = end;
hash[end] = n;
n++;
}
int targetnode = hash[end]; //记录终点的节点编号,便于提前返回
// cout<<n<<endl;
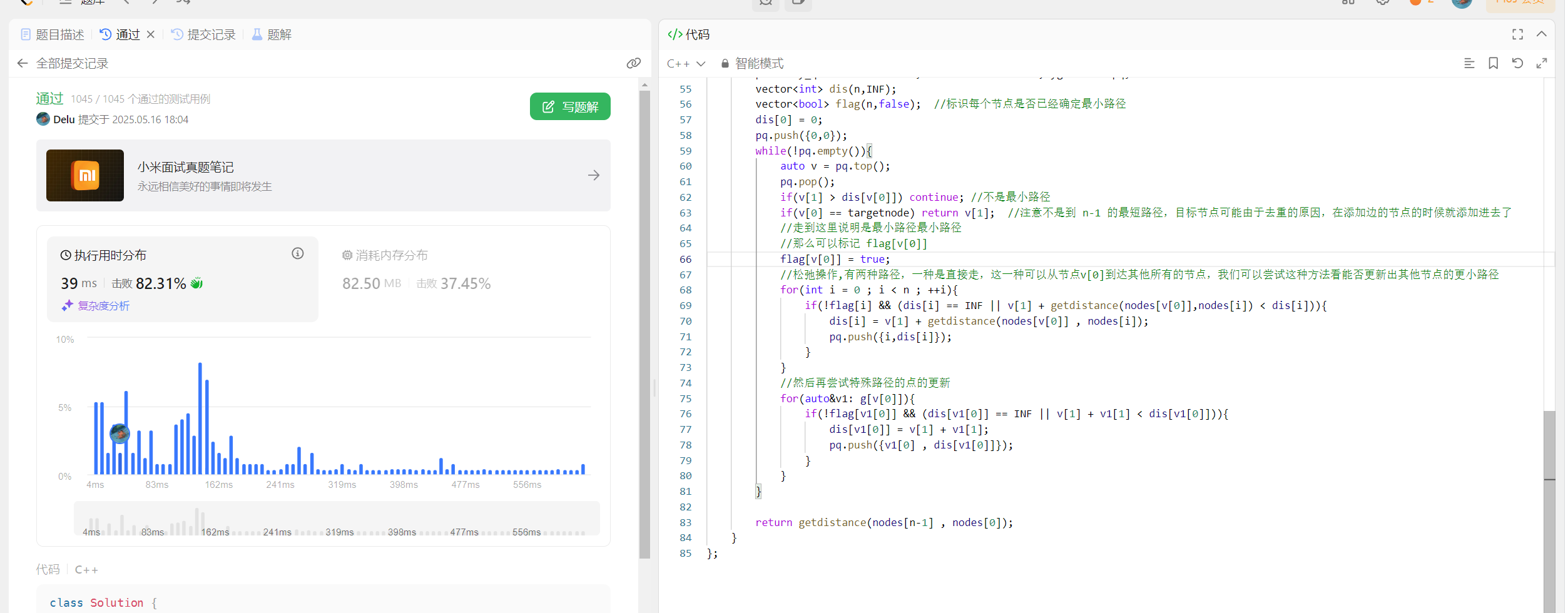
//接下来做Dijkstra
priority_queue<vector<int>,vector<vector<int>>,mygreater> pq;
vector<int> dis(n,INF);
vector<bool> flag(n,false); //标识每个节点是否已经确定最小路径
dis[0] = 0;
pq.push({0,0});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
if(v[1] > dis[v[0]]) continue; //不是最小路径
if(v[0] == targetnode) return v[1]; //注意不是到 n-1 的最短路径,目标节点可能由于去重的原因,在添加边的节点的时候就添加进去了
//走到这里说明是最小路径最小路径
//那么可以标记 flag[v[0]]
flag[v[0]] = true;
//松弛操作,有两种路径,一种是直接走,这一种可以从节点v[0]到达其他所有的节点,我们可以尝试这种方法看能否更新出其他节点的更小路径
for(int i = 0 ; i < n ; ++i){
if(!flag[i] && (dis[i] == INF || v[1] + getdistance(nodes[v[0]],nodes[i]) < dis[i])){
dis[i] = v[1] + getdistance(nodes[v[0]] , nodes[i]);
pq.push({i,dis[i]});
}
}
//然后再尝试特殊路径的点的更新
for(auto&v1: g[v[0]]){
if(!flag[v1[0]] && (dis[v1[0]] == INF || v[1] + v1[1] < dis[v1[0]])){
dis[v1[0]] = v[1] + v1[1];
pq.push({v1[0] , dis[v1[0]]});
}
}
}
return getdistance(nodes[n-1] , nodes[0]);
}
};
启示
对于这类型图中的节点十分多,大部分节点之间的路径是一个可预测的长度,而有一些特殊路径的长度有题目给出,那么我们就可以尝试先建图,再去思考使用上面算法来求解最短路径的问题。
13 使两个整数相等的数位操作
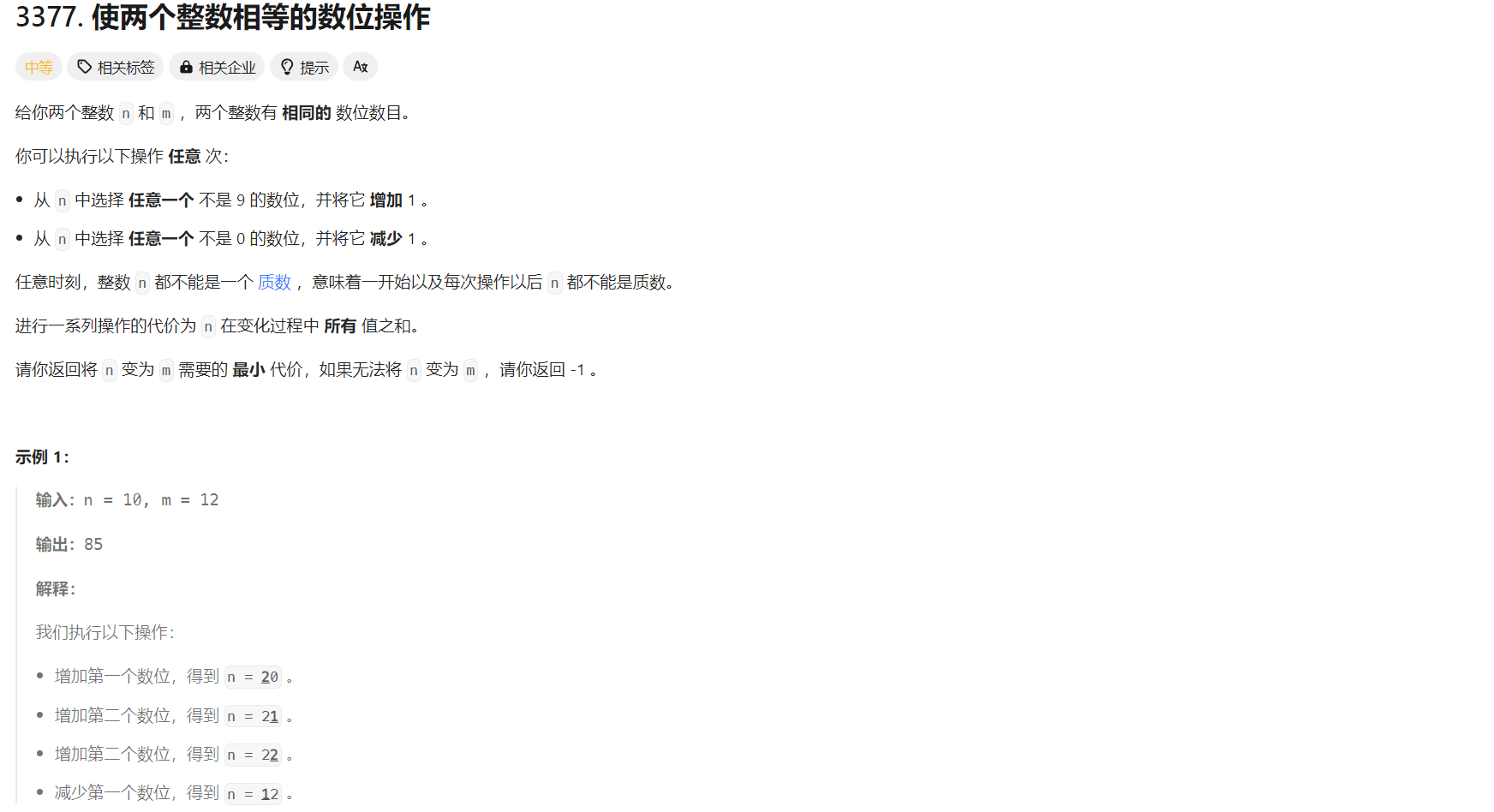

题目解析:题目意思很简单,给定两个数位个数相同的整数 m 和 n ,要求我们将m转换为 n,只能对m某个数位进行+1或者-1,返回最少的操作代价,总的操作代价就是在转换过程中的所有的值的总和,要求在中间过程中n不能是质数。
本题怎么使用Dijkstra来完成呢?
因为题目限制 m 和 n 都是小于10000的,把和 m 数位个数相同的所有整数看成是图的节点,最多也就是 9000 个节点,而每一个节点(除了质数)都有边连接向 进行一次数位操作能够相同的节点,边的权值为1。当然其实并没有
但是题目还有一个要求就是不能对 9 加一也不能对 0减一。
本题还要求转换过程中不能是质数,所以我们需要标识一下所有的质数。
质数的筛法常用的有两种: 埃式筛和欧拉筛,这里我们直接使用欧拉筛来完成,在全局使用lambda表达式来进行筛选。
bool flag[10001] ={false};
int init =[&]{
flag[1] = true; //为true表示是质数,否则为合数
for(int i = 2 ; i < 10000; ++i){
if(!flag[i]){
for(int j = i * i ; j < 10001 ; j += i) flag[j] = true; //j为合数,j = i * (i + x)
}
}
return 0;
}();然后我们就需要完成Dijkstra的过程,起点无非就是n,n所需的数位操作代价为n自身,然后不断根据出堆的数据x的操作代价,来更新x的邻节点,也就是x经过一次数位操作能够转换的数据。
题目还有一个很大的坑,就是在转换过程中,位数不能减少,也就是如果是第一位为1,我们其实不能将其减到0,这一点题目中似乎没有说明。
代码如下:
class Solution {
public:
bool flag[10001] ={false};
int init =[&]{
//为true表示是合数,否则为质数
flag[1] = true;
for(int i = 2 ; i <= 10000; ++i){
if(!flag[i]){
for(int j = i * i ; j < 10001 ; j += i) flag[j] = true; //j为合数,j = i * (i + x)
}
}
return 0;
}();
class mygreater{
public:
bool operator()(const vector<int>& v1 , const vector<int>& v2){return v1[1] > v2[1];}
};
const int INF = 0x3f3f3f3f;
int minOperations(int n, int m) {
if(!flag[m]) return -1; //质数不可达
vector<int> dis(10001,INF);
dis[n] = n;
int len = 0 ; //求n的位数,方便后续操作
int n1 = n;
while(n1){
n1/=10;
len ++;
}
priority_queue<vector<int>,vector<vector<int>> ,mygreater>pq;
pq.push({n,n});
while(!pq.empty()){
auto v = pq.top();
pq.pop();
int x = v[0] , cost = v[1];
if(x == m) return cost; //提前返回
if(!flag[x]) continue; //x是质数的话不可达
if(cost > dis[x]) continue; //不是第一次出堆
//然后开始进行加一和减一的操作
//取出x的每一个数位
int prevnum = x , backnum = 0 ; //将数字分成两部分看,对前部分加一减一 *pow(10,i) ,然后加上后面一部分
for(int i = 0 ; i < len ; ++i){
if(prevnum % 10 < 9){ //前半部分可以进行加一操作
int prev = prevnum + 1;
int total = prev * pow(10,i) + backnum; //组合成新的数
if(flag[total] && dis[total] > cost + total){
dis[total] = cost + total;
pq.push({total,dis[total]});
}
}
if(prevnum % 10 > 0){
int prev = prevnum - 1;
int total = prev * pow(10,i) + backnum;
if(prev != 0){
if(flag[total] && dis[total] > cost + total){
dis[total] = cost + total;
pq.push({total , dis[total]});
}
}
}
backnum += ((prevnum%10) * pow(10,i));
prevnum /= 10;
}
}
return -1;
}
};
后续如果看到有价值的题目会继续更新在本文

























 926
926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










