动手学深度学习笔记3——线性代数

Charles~Yang

已于 2023-04-04 21:48:27 修改

阅读量243

点赞数

文章标签：深度学习线性代数人工智能

于 2023-04-04 21:35:51 首次发布

本文链接：https://blog.csdn.net/weixin_66472769/article/details/129960345

版权

1.线性代数

本节将介绍线性代数中的基本数学对象、算术和运算，并⽤数学符号和相应的代码实现来表⽰它们。

1.1标量

本书采用了数学表示法，其中标量变量由普通小写字母表示（例如，x、y和z）。本书用R表示所有（连续）实数标量的空间，之后将严格定义空间（space）是什么，但现在只要记住表达式x∈R是表示x是一个实值标量的正式形式。

标量由只有一个元素的张量表示。下面的代码将实例化两个标量，并执行一些熟悉的算术运算，即加法、乘法、除法和指数。

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x**y

(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))

1.2向量

向量可以被视为标量值组成的列表。这些标量值被称为向量的元素（element）或分量（component）。在数学表⽰法中，向量通常记为粗体、⼩写的符号（例如，x、y和z)）。

⼈们通过⼀维张量表⽰向量。⼀般来说，张量可以具有任意⻓度，取决于机器的内存限制。

x = torch.arange(4)
x

tensor([0, 1, 2, 3])

我们可以使⽤下标来引⽤向量的任⼀元素，例如可以通过 $xi$ 来引⽤第i个元素。注意，元素 $xi$ 是⼀个标量，所以我们在引⽤它时不会加粗。⼤量⽂献认为列向量是向量的默认⽅向，在本书中也是如此。在数学中，向量x可以写为：

其中x1, . . . , xn是向量的元素。在代码中，我们通过张量的索引来访问任⼀元素

x[3]

tensor(3)

向量只是⼀个数字数组，就像每个数组都有⼀个⻓度⼀样，每个向量也是如此。在数学表⽰法中，如果我们想说⼀个向量x由n个实值标量组成，可以将其表⽰为x ∈ $\mathbb{R}$ n。向量的⻓度通常称为向量的维度（dimension）。与普通的Python数组⼀样，我们可以通过调⽤Python的内置len()函数来访问张量的⻓度。

len(x)

4

当⽤张量表⽰⼀个向量（只有⼀个轴）时，我们也可以通过.shape属性访问向量的⻓度。形状（shape）是⼀个元素组，列出了张量沿每个轴的⻓度（维数）。对于只有⼀个轴的张量，形状只有⼀个元素。

x.shape

torch.Size([4])

向量或轴的维度被⽤来表⽰向量或轴的⻓度，即向量或轴的元素数量。然⽽，张量的维度⽤来表⽰张量具有的轴数。在这个意义上，张量的某个轴的维数就是这个轴的⻓度。

1.3矩阵

矩阵，我们通常⽤粗体、⼤写字⺟来表⽰（例如，X、Y和Z），在代码中表⽰为具有两个轴的张量。数学表⽰法使⽤A ∈ $\mathbb{R}^{m\times n}$ 来表⽰矩阵A，其由m⾏和n列的实值标量组成。我们可以将任意矩阵A ∈ $\mathbb{R}^{m\times n}$ 视为⼀个表格，其中每个元素 $a_{ij}$ 属于第i⾏第j列：

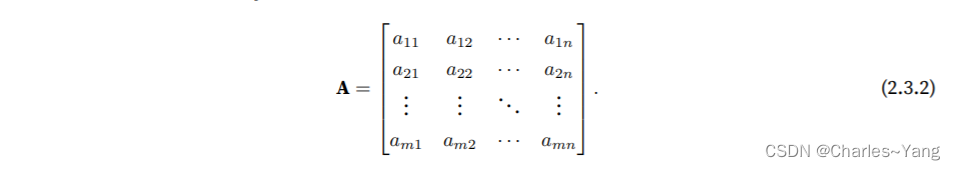
对于任意A ∈ $\mathbb{R}^{m\times n}$ ，A的形状是（m,n）或m × n。当矩阵具有相同数量的⾏和列时，其形状将变为正⽅形；因此，它被称为⽅阵（square matrix）。当调⽤函数来实例化张量时，我们可以通过指定两个分量m和n来创建⼀个形状为m × n的矩阵。

A = torch.arange(20).reshape(5, 4)
A

tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])

当我们交换矩阵的⾏和列时，结果称为矩阵的转置（transpose）。通常⽤a ⊤来表⽰矩阵的转置，如果B = A ⊤，则对于任意i和j，都有bij = aji。因此，在 (2.3.2)中的转置是⼀个形状为n × m的矩阵：

在代码中访问矩阵的转置

A.T

tensor([[ 0,  4,  8, 12, 16],
        [ 1,  5,  9, 13, 17],
        [ 2,  6, 10, 14, 18],
        [ 3,  7, 11, 15, 19]])

作为⽅阵的⼀种特殊类型，对称矩阵（symmetric matrix）A等于其转置：A = A ⊤。这⾥定义⼀个对称矩阵B：

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B

tensor([[1, 2, 3],
        [2, 0, 4],
        [3, 4, 5]])

现在我们将B与它的转置进⾏⽐较。

B == B.T

tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])

1.4张量

张量（本⼩节中的 “张量”指代数对象）是描述具有任意数量轴的n维数组的通⽤⽅法。张量⽤特殊字体的⼤写字⺟表⽰（例如，X、Y和Z）。

X = torch.arange(24).reshape(2, 3, 4)
X

tensor([[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7],
         [ 8,  9, 10, 11]],

        [[12, 13, 14, 15],
         [16, 17, 18, 19],
         [20, 21, 22, 23]]])

1.5张量算法的基本性质

给定具有相同形状的任意两个张量，任何按元素⼆元运算的结果都将是相同形状的张量。

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存，将A的⼀个副本分配给B
A, A + B

(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  2.,  4.,  6.],
         [ 8., 10., 12., 14.],
         [16., 18., 20., 22.],
         [24., 26., 28., 30.],
         [32., 34., 36., 38.]]))

两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号⊙）。对于矩阵B ∈ $\mathbb{R}^{m\times n}$ ，其中第i⾏和第j列的元素是bij。矩阵A和B的Hadamard积为：

A * B

tensor([[  0.,   1.,   4.,   9.],
        [ 16.,  25.,  36.,  49.],
        [ 64.,  81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])

将张量乘以或加上⼀个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

(tensor([[[ 2,  3,  4,  5],
          [ 6,  7,  8,  9],
          [10, 11, 12, 13]],

         [[14, 15, 16, 17],
          [18, 19, 20, 21],
          [22, 23, 24, 25]]]),
 torch.Size([2, 3, 4]))

1.6降维

1.6.1降维求和

我们可以对任意张量进⾏的⼀个有⽤的操作是计算其元素的和。数学表⽰法使⽤∑符号表⽰求和。为了表⽰⻓度为d的向量中元素的总和，可以记为 $\sum_{i=1}^{d}x_{i}$ 。在代码中可以调⽤计算求和的函数：

x = torch.arange(4, dtype=torch.float32)
x, x.sum()

(tensor([0., 1., 2., 3.]), tensor(6.))

我们可以表⽰任意形状张量的元素和。例如，矩阵A中元素的和可以记为∑m i=1 ∑n j=1 aij。

A.shape, A.sum()

(torch.Size([5, 4]), tensor(190.))

默认情况下，调⽤求和函数会沿所有的轴降低张量的维度，使它变为⼀个标量。我们还可以指定张量沿哪⼀个轴来通过求和降低维度。以矩阵为例，为了通过求和所有⾏的元素来降维（轴0），可以在调⽤函数时指定axis=0。由于输⼊矩阵沿0轴降维以⽣成输出向量，因此输⼊轴0的维数在输出形状中消失。

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

(tensor([40., 45., 50., 55.]), torch.Size([4]))

指定axis=1将通过汇总所有列的元素降维（轴1）。因此，输⼊轴1的维数在输出形状中消失。

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))

沿着⾏和列对矩阵求和，等价于对矩阵的所有元素进⾏求和。

A.sum(axis=[0, 1]) # 结果和A.sum()相同

tensor(190.)

⼀个与求和相关的量是平均值（mean或average）。我们通过将总和除以元素总数来计算平均值。在代码中，我们可以调⽤函数来计算任意形状张量的平均值。

A.mean(), A.sum() / A.numel()

(tensor(9.5000), tensor(9.5000))

同样，计算平均值的函数也可以沿指定轴降低张量的维度。

A.mean(axis=0), A.sum(axis=0) / A.shape[0]

(tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))

1.6.2非降维求和

有时在调⽤函数来计算总和或均值时保持轴数不变会很有⽤。

sum_A = A.sum(axis=1, keepdims=True)
sum_A

tensor([[ 6.],
        [22.],
        [38.],
        [54.],
        [70.]])

如果我们想沿某个轴计算A元素的累积总和，⽐如axis=0（按⾏计算），可以调⽤cumsum函数。此函数不会沿任何轴降低输⼊张量的维度。

A.cumsum(axis=0)

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  6.,  8., 10.],
        [12., 15., 18., 21.],
        [24., 28., 32., 36.],
        [40., 45., 50., 55.]])

1.7点积

给定两个向量x, y ∈ $\mathbb{R}^{d}$ ，它们的点积（dot product）x ⊤y （或〈x, y〉）是相同位置的按元素乘积的和：x ⊤y = $\sum_{i=1}^{d}x_{i}y_{i}$ 。

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))

注意，我们可以通过执⾏按元素乘法，然后进⾏求和来表⽰两个向量的点积：

torch.sum(x * y)

tensor(6.)

给定⼀组由向量x ∈ $\mathbb{R}^{d}$ 表⽰的值，和⼀组由w ∈ $\mathbb{R}^{d}$ 表⽰的权重。x中的值根据权重w的加权和，可以表⽰为点积x ⊤w。当权重为⾮负数且和为1（即( $\sum_{i=1}^{d}w_{i}=1$ ) ）时，点积表⽰加权平均（weighted average）。将两个向量规范化得到单位⻓度后，点积表⽰它们夹⻆的余弦： $cos(\Theta)=\frac{a\cdot b}{\left \| a \right \|\left \| b \right \|}$ 。

1.8矩阵-向量积

回顾分别在 (1.2)和 (1.1)中定义的矩阵A ∈ $\mathbb{R}^{m\times n}$ 和向量x ∈ $\mathbb{R}^{n}$ 。让我们将矩阵A⽤它的⾏向量表⽰：

其中每个 $a_{i}^{T}$ ∈ $\mathbb{R}^{n}$ 都是⾏向量，表⽰矩阵的第i⾏。矩阵向量积Ax是⼀个⻓度为m的列向量，其第i个元素是点积 $a_{i}^{T}$ x：

我们可以把⼀个矩阵A ∈ $\mathbb{R}^{m\times n}$ 乘法看作⼀个从 $\small \mathbb{R}^{n}$ 到 $\small \mathbb{R}^{m}$ 向量的转换。这些转换是⾮常有⽤的，例如可以⽤⽅阵的乘法来表⽰旋转。后续章节将讲到，我们也可以使⽤矩阵-向量积来描述在给定前⼀层的值时，求解神经⽹络每⼀层所需的复杂计算。在代码中使⽤张量表⽰矩阵-向量积，我们使⽤mv函数。当我们为矩阵A和向量x调⽤torch.mv(A, x)时，会执⾏矩阵-向量积。注意，A的列维数（沿轴1的⻓度）必须与x的维数（其⻓度）相同。

A.shape, x.shape, torch.mv(A, x)

(torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))

1.9矩阵-矩阵乘法

假设有两个矩阵A ∈ $\small \mathbb{R}^{n\times k}$ 和B ∈ $\small \mathbb{R}^{k\times m}$ ：

⽤⾏向量 $\small a_{i}^{T}$ ∈ $\small \mathbb{R}^{k}$ 表⽰矩阵A的第i⾏，并让列向量bj ∈ $\small \mathbb{R}^{k}$ 作为矩阵B的第j列。要⽣成矩阵积C = AB，最简单的⽅法是考虑A的⾏向量和B的列向量:

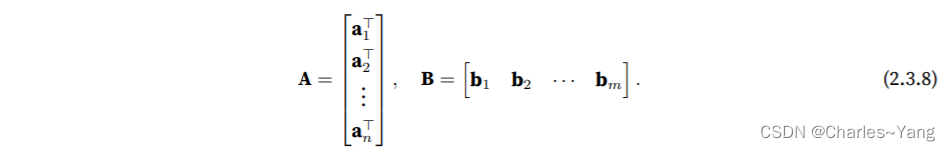
当我们简单地将每个元素cij计算为点积 $\small a^{T}_{i}$ $\small b_{j}$ :

我们可以将矩阵-矩阵乘法AB看作简单地执⾏m次矩阵-向量积，并将结果拼接在⼀起，形成⼀个n × m矩阵。在下⾯的代码中，我们在A和B上执⾏矩阵乘法。这⾥的A是⼀个5⾏4列的矩阵，B是⼀个4⾏3列的矩阵。两者相乘后，我们得到了⼀个5⾏3列的矩阵。

B = torch.ones(4, 3)
torch.mm(A, B)

tensor([[ 6.,  6.,  6.],
        [22., 22., 22.],
        [38., 38., 38.],
        [54., 54., 54.],
        [70., 70., 70.]])

矩阵-矩阵乘法可以简单地称为矩阵乘法，不应与”Hadamard积”混淆。

1.10范数

线性代数中最有⽤的⼀些运算符是范数（norm）。⾮正式地说，向量的范数是表⽰⼀个向量有多⼤。这⾥考虑的⼤⼩（size）概念不涉及维度，⽽是分量的⼤⼩。

在线性代数中，向量范数是将向量映射到标量的函数f。给定任意向量x，向量范数要满⾜⼀些属性。第⼀个性质是：如果我们按常数因⼦α缩放向量的所有元素，其范数也会按相同常数因⼦的绝对值缩放：

第⼆个性质是熟悉的三⻆不等式:

第三个性质简单地说范数必须是⾮负的:

因为在⼤多数情况下，任何东西的最⼩的⼤⼩是0。最后⼀个性质要求范数最⼩为0，当且仅当向量全由0组成。

范数听起来很像距离的度量。欧⼏⾥得距离和毕达哥拉斯定理中的⾮负性概念和三⻆不等式可能会给出⼀些启发。事实上，欧⼏⾥得距离是⼀个L2范数：假设n维向量x中的元素是x1, . . . , xn，其L2范数是向量元素平⽅和的平⽅根：

其中，在L2范数中常常省略下标2，也就是说∥x∥等同于∥x∥2。在代码中，我们可以按如下⽅式计算向量的L2范数。

u = torch.tensor([3.0, -4.0])
torch.norm(u)

tensor(5.)

深度学习中更经常地使⽤L2范数的平⽅，也会经常遇到L1范数，它表⽰为向量元素的绝对值之和：

与L2范数相⽐，L1范数受异常值的影响较⼩。为了计算L1范数，我们将绝对值函数和按元素求和组合起来。

torch.abs(u).sum()

tensor(7.)

L2范数和L1范数都是更⼀般的Lp范数的特例：

类似于向量的L2范数，矩阵X ∈ R m×n的Frobenius范数（Frobenius norm）是矩阵元素平⽅和的平⽅根：

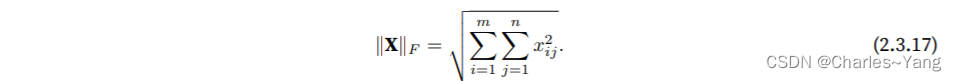
Frobenius范数满⾜向量范数的所有性质，它就像是矩阵形向量的L2范数。调⽤以下函数将计算矩阵的Frobenius范数。

torch.norm(torch.ones((4, 9)))

tensor(6.)

在深度学习中，我们经常试图解决优化问题：最⼤化分配给观测数据的概率; 最⼩化预测和真实观测之间的距离。⽤向量表⽰物品（如单词、产品或新闻⽂章），以便最⼩化相似项⽬之间的距离，最⼤化不同项⽬之间的距离。⽬标，或许是深度学习算法最重要的组成部分（除了数据），通常被表达为范数。

1.11关于线性代数的更多信息

线性代数还有很多，其中很多数学对于机器学习⾮常有⽤。例如，矩阵可以分解为因⼦，这些分解可以显⽰真实世界数据集中的低维结构。机器学习的整个⼦领域都侧重于使⽤矩阵分解及其向⾼阶张量的泛化，来发现数据集中的结构并解决预测问题。当开始动⼿尝试并在真实数据集上应⽤了有效的机器学习模型，你会更倾向于学习更多数学。