💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
多基地雷达系统的周期性多相位调制有源欺骗干扰研究
摘要:
针对多基地雷达系统中虚假目标(FT)的幅度在接收机之间相关的问题,提出了一种基于周期多相位调制(PMPM)的多干扰机协作欺骗干扰方法。在信号经过PMPM处理后,可以生成一个振幅随机波动的FT字符串。在分布式干扰系统中,每个干扰机采用不同参数的PMPM干扰方法,然后联合发射波束形成,转发干扰信号。最后,接收机之间的傅里叶变换的幅度受到方位角和相位调制系数的共同影响,破坏了接收机之间傅里叶变换的幅度“相干性”,消除了传统干扰方法产生的傅里叶变换串的幅度对称性和高阶衰减特性。我们研究了所提出的干扰方法的幅度补偿和幅度相关性能,推导出了幅度相关因子比率矩阵的秩,并证明了傅里叶变换在幅度比空间中具有色散性。为了获得最佳和稳定的干扰效果,设计了一种基于遗传算法的干扰调制参数优化方法,该方法有效地将物理目标(PT)的鉴别概率降低到基准场景中的14%。仿真实验证明了干扰方法的可行性和有效性。
Abstract:
Aiming at the problem that the amplitudes of false targets (FTs) are correlated among receivers in multistatic radar system, a multijammer cooperative deception jamming method based on periodic multiple phases modulation (PMPM) is proposed. A FT string with random fluctuations in amplitude can be generated after the signal undergoes PMPM. In the distributed jammer system, each jammer adopts PMPM jamming method with different parameters, and then jointly transmit beamforming to forward jamming signals. Finally, the amplitude of the FTs between receivers is jointly affected by the azimuth angle and the phase modulation coefficient, which destroys the amplitude “coherence” of the FTs between receivers, and eliminates the amplitude symmetry and high-order attenuation characteristics of the FT strings generated by traditional jamming method. We study the amplitude compensation and amplitude correlation performance of the proposed jamming method, derive the rank of the ratio matrix of amplitude correlation factors, and prove that FTs have dispersiveness in the amplitude ratio space. In order to obtain the optimal and stable jamming effect, a genetic algorithm based jamming modulation parameter optimization method is designed, which effectively drops the discrimination probability of physical targets (PTs) to 14% in the benchmark scenario. Simulation experiments demonstrate the feasibility and effectiveness of the jamming method.
多基地雷达系统(MSRS)是一种集成雷达系统,具有多个空间上分离的发射和接收天线接收设施[1]、[2]。与传统相比单基地雷达,MSRS提供了更多的自由度,因此,它在移动目标检测、测向和目标定位方面具有显著的优势[3]。然而,事实上,一些重要的建筑物、机场和军事设施预计目标不会受到MSRS的监测。因此,需要针对MSRS的电子对抗措施考虑过的。一般来说,电子对抗干扰方法可被归类为拦阻干扰或欺骗基于干扰效果的干扰。拦阻式干扰产生类似噪声的干扰效果,需要高发射功率。欺骗干扰信号非常强与目标回波信号相关,可以获得匹配增益。特别是基于数字射频存储器(DRFM)的多假目标欺骗干扰技术不仅保留了回声特性物理目标(PTs)并可被利用来迷惑雷达系统,而且增加了识别负担PTs浪费了雷达的有限资源。什么时候?受欺骗干扰的威胁,MSRS被认为是有效的对策。只要MSRS有相对于目标的足够不同的视角,每个雷达接收到的目标信号是不相关的。自从干扰信号是由同一个干扰机产生的每个雷达接收到的干扰信号都是相互关联的彼此[4],[5]。根据这一原则,MSRS发现干扰信号与目标之间的差异信号处理单元100接收不同信号电平的信号, 并对其进行区分。例如,在基于以下内容建立的特征空间中振幅比差,PT具有分散特性,而假目标(FT)具有集中特性特征,特别适合使用无监督学习方法来有效地识别欺骗行为干扰[6]、[7]。理论分析和模拟验证了使用这种方法进行MSRS的有效性,因此制定针对MSRS的新对策成为不断增长的需求。详细文章见第4部分。


1. 多基地雷达系统的定义与工作原理
多基地雷达系统(Multistatic Radar System, MSRS)由分布于不同地理位置的发射机和接收机组成,其发射机和接收机数量可不相等,且通过协同工作实现目标探测与定位。相较于单基地雷达,多基地系统具有以下特性:
- 几何构型优势:通过多角度观测提高目标探测概率和精度,克服单基地雷达的几何模糊问题。
- 抗干扰能力:多节点数据融合可抑制干扰信号,单一干扰源难以同时欺骗所有接收站。
- 高精度定位:利用距离差、角度差等多参数融合,实现远距离目标精确定位。
- 关键挑战:包括复杂的数据处理系统、天线副瓣干扰严重、虚假目标问题(幻象交点)等。
2. 周期性多相位调制技术(PMPM)的核心机制
周期性多相位调制是一种多进制数字相位调制技术,通过载波相位的周期性变化传递信息,其特点包括:
- 数学表达式:调制信号可表示为 s(t)=exp(j2πf0t+jϕ(t))s(t)=exp(j2πf0t+jϕ(t)),其中 ϕ(t)ϕ(t) 为周期性相位序列。
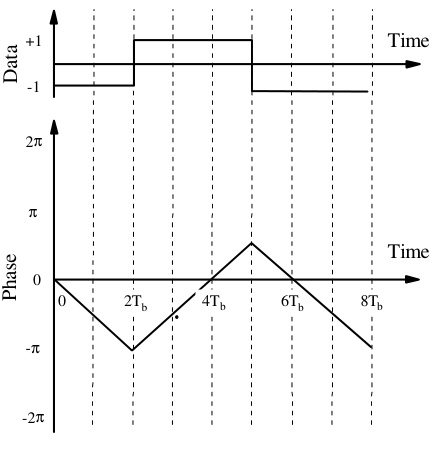
- 应用优势:
- 高欺骗性:通过精确控制相位序列,生成与真实目标回波相似的信号。
- 灵活性:支持脉间、脉内调制,适用于合成孔径雷达(SAR)和多基地雷达的干扰场景。
- 抗相关性抑制:破坏多基地雷达系统中虚假目标的幅度关联性,降低干扰被识别的概率。
3. 有源欺骗干扰的实现方式与特点
有源欺骗干扰通过数字射频存储器(DRFM)截获雷达信号,生成时/频/空域逼真的假目标,具体实现方式包括:
- 射频转发干扰:通过DRFM存储并转发雷达信号,在真实目标周围生成多个假目标。
- 周期多相位调制干扰:利用PMPM技术生成随机起伏的虚假目标串,破坏多基地雷达的幅度相关性。
- 协同干扰:多干扰机协作,通过参数差异化配置增强干扰效果。
4. 多基地雷达系统的关键干扰环节
- 信号接收与融合环节:干扰信号可能通过接收机副瓣或主瓣进入系统,影响数据融合的准确性。
- 虚假目标关联性:传统干扰生成的假目标在幅度上具有相关性,易被多基地系统识别。
- 极化与频率敏感性:干扰信号与真实目标的极化特性差异可能被利用进行鉴别。
5. 周期性多相位调制的干扰效能评估
- 仿真验证:通过Matlab仿真表明,PMPM干扰可在SAR成像中生成距离向、方位向二维分布的假目标,且幅度随机起伏,显著提高干扰隐蔽性。
- 幅度关联性破坏:干扰后虚假目标的幅度关联因子比值矩阵秩增大,导致目标识别失败概率降低。
- 遗传算法优化:结合遗传算法优化调制参数,可进一步提升干扰稳定性。
6. 现有研究成果与关键技术
- 梅胜群的研究:提出基于PMPM的SAR干扰方法,通过相位序列调制生成非对称假目标串,并验证了其对多基地雷达系统的有效性。
- 协同干扰策略:多干扰机采用差异化PMPM参数,联合波束成形转发信号,增强干扰覆盖范围。
- 抗干扰识别算法:基于统计相关性差异(如幅度序列相关性检测)的干扰识别方法,虚警率可控制在1%以下。
7. 多基地雷达系统的抗干扰措施
- 空间与极化分集:利用多节点空间分布和极化特性差异抑制干扰。
- 频率捷变技术:快速切换工作频率,避免干扰信号锁定。
- 智能信号处理:采用空时自适应处理(STAP)和深度学习算法增强干扰识别。
- 数据融合优化:改进融合算法,剔除异常数据点,降低干扰影响。
8. 未来研究方向
- 智能化干扰对抗:结合深度学习与强化学习,实现动态干扰策略优化。
- 多维度联合识别:融合极化、多普勒、时频特征,提升干扰鉴别鲁棒性。
- 新型调制技术:探索混沌相位调制等非线性方法,增强干扰信号的不可预测性。
总结
周期性多相位调制有源欺骗干扰通过破坏多基地雷达系统的数据关联性,显著提升了干扰效能。现有研究在干扰生成、协同策略和抗干扰识别算法方面取得重要进展,但仍需进一步结合智能化技术与多维度特征融合以应对复杂对抗环境。未来,多基地雷达系统的抗干扰能力提升将依赖于技术创新与多学科交叉研究。
📚2 运行结果

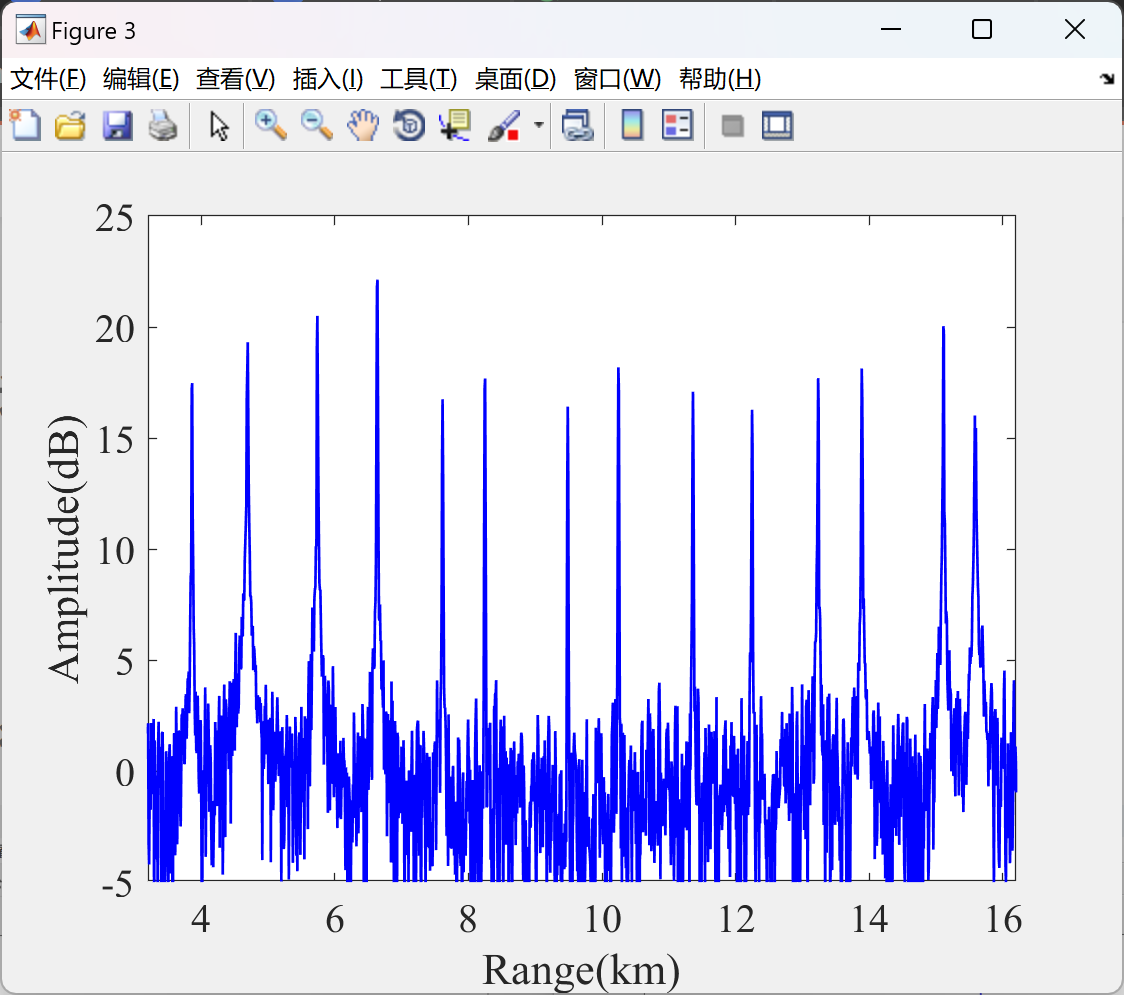





部分代码:
c=3e+8; % 光速
pi=3.1415926; % pi
Tp=100e-6; % 发射脉冲宽度
fc=5e+9; % 载频 满足机载雷达工作频率
FsrFactor = 1; % 距离方向上的过采样率
FsaFactor = 1; % 方位方向上的过采样率
wintype='hamming'; % 窗类型
lamda=c/fc; % 波长
Br=20e6; % 所需的传输带宽
Fs=Br*FsrFactor; % A / D采样率
Kr=Br/Tp; % 距离chirp斜率chirp:脉冲压缩
% 雷达位置
r1 = [0, 0, 0]; % 主雷达的位置
r2 = [2e3, 4e3, 0]; % 附属雷达2的位置
r3 = [3e3, 2e3, 0]; % 附属雷达3的位置
% 干扰机位置
jammer = [4e3, 5e3, 7e3];
distance = 2*sqrt((jammer(1)-r1(1))^2 + (jammer(2)-r1(2))^2 +(jammer(3)-r1(3))^2);
rstart=distance/c-Tp/2;
rend=distance/c+Tp/2;
rsample_t=rstart:1/Fs:rend; % 距离向采样时间
rsample_d=rsample_t*c/2; % 距离向采样距离
nr=length(rsample_t); % 距离向采样点数217
N = 6; % 分布式干扰机个数
d = 100; % 满足干扰通道独立的条件,L>lamda*R/D
% 计算各雷达到干扰机的角度,以干扰机为原点,计算与各雷达的方位角
theta1 = atan((jammer(1)-r1(1))/(jammer(2)-r1(2)))*180/pi; % 主雷达到干扰机的方位角,角度值
theta2 = atan((jammer(1)-r2(1))/(jammer(2)-r2(2)))*180/pi; % 附属雷达2到干扰机的方位角,角度值
theta3 = atan((jammer(1)-r3(1))/(jammer(2)-r3(2)))*180/pi; % 附属雷达3到干扰机的方位角,角度值
% 生成干扰机阵列导向矢量
n=(0:N-1)'; % 阵元位置
a_theta1=exp(2*pi*1j*(d/lamda)*n*sin(theta1*pi/180));
a_theta2=exp(2*pi*1j*(d/lamda)*n*sin(theta2*pi/180));
a_theta3=exp(2*pi*1j*(d/lamda)*n*sin(theta3*pi/180));
disR1J = sqrt((jammer(1)-r1(1))^2 + (jammer(2)-r1(2))^2 + (jammer(3)-r1(3))^2);
time_delayR1J = 2*disR1J/c;
jamR = exp(1i*pi*Kr*(rsample_t-time_delayR1J).^2);
%周期多相位随机分段调制干扰
T0=0.4e-6; %矩形脉冲宽度 0.1us
K_tao=floor(T0*Fs);
Q = 8; % 周期内随机分段数
N_tao = [1,1,1,1,1,1,1,1];
M=floor(nr/K_tao); %周期个数
fr=linspace(-Fs/2,Fs/2,nr);
Hr=exp(-1i*pi*fr.^2/Kr)'.*feval(wintype,nr);
% 干扰机1→主雷达
SNR1 = 25;
%前面程序中真实信号生成的幅度比
truem=[0.898355661363199,0.584296289779643;2.19262699239795,4.13783594838136;1.20406349556595,3.30060167090429;0.754118784451319,2.11840519807012;2.45895179393671,3.18377857842292;0.0884163051834587,0.0735130899665708;0.565924773269425,1.33916358220479];
%% 遗传算法-多变量优化
number_of_variables = N*Q; % 求解问题的参数个数
population_size = 160; % 种群规模(每一代个体数目)
parent_number = 80; % 每一代中保持不变的数目(除了变异)
mutation_rate = 0.01; % 变异概率
maximal_generation = 5; % 最大演化代数
minimal_cost = 0.1; % 最小目标值(函数值越小,则适应度越高)
% gap_plot = 25;
% Accuracy = zeros(1,maximal_generation/gap_plot);
% Precision = zeros(1,maximal_generation/gap_plot);
% Recall = zeros(1,maximal_generation/gap_plot);
% F1_score = zeros(1,maximal_generation/gap_plot);
% u = 1;
% 累加概率
% 假设 parent_number = 10
% 分子 parent_number:-1:1 用于生成一个数列
% 分母 sum(parent_number:-1:1) 是一个求和结果(一个数)
%
% 分子 10 9 8 7 6 5 4 3 2 1
% 分母 55
% 相除 0.1818 0.1636 0.1455 0.1273 0.1091 0.0909 0.0727 0.0545 0.0364 0.0182
% 累加 0.1818 0.3455 0.4909 0.6182 0.7273 0.8182 0.8909 0.9455 0.9818 1.0000
%
% 运算结果可以看出
% 累加概率函数是一个从0到1增长得越来越慢的函数
% 因为后面加的概率越来越小(数列是降虚排列的)
cumulative_probabilities = cumsum((parent_number:-1:1) / sum(parent_number:-1:1)); % 1个长度为parent_number的数列
% 最佳适应度
% 每一代的最佳适应度都先初始化为1
best_fitness = ones(maximal_generation, 1);
% 精英
% 每一代的精英的参数值都先初始化为0
elite = zeros(maximal_generation, number_of_variables);
% 子女数量
% 种群数量 - 父母数量(父母即每一代中不发生改变的个体)
child_number = population_size - parent_number; % 每一代子女的数目
% 初始化种群
% population_size 对应矩阵的行,每一行表示1个个体,行数=个体数(种群数量)
% number_of_variables 对应矩阵的列,列数=参数个数(个体特征由这些参数表示)
population = 2*rand(population_size, number_of_variables);
% 十进制编码
population = round(population.*10^3);
last_generation = 0; % 记录跳出循环时的代数
% 后面的代码都在for循环中
for generation = 1 : maximal_generation % 演化循环开始
% 计算适应度
fitness = zeros(1,population_size);
for i = 1 : size(population,1)
rand_num = population(i,:);
rand_num_i = reshape(rand_num,Q,N);
bk = exp(1i*rand_num_i.'/10^3*pi);
a1=[];a2=[];a3=[];a4=[];a5=[];a6=[];
for m=1:Q
a1= cat(2,a1,bk(1,m).*ones(1,N_tao(m)*(K_tao/sum(N_tao))));
a2= cat(2,a2,bk(2,m).*ones(1,N_tao(m)*(K_tao/sum(N_tao))));
a3= cat(2,a3,bk(3,m).*ones(1,N_tao(m)*(K_tao/sum(N_tao))));
a4= cat(2,a4,bk(4,m).*ones(1,N_tao(m)*(K_tao/sum(N_tao))));
a5= cat(2,a5,bk(5,m).*ones(1,N_tao(m)*(K_tao/sum(N_tao))));
a6= cat(2,a6,bk(6,m).*ones(1,N_tao(m)*(K_tao/sum(N_tao))));
end
pss_r1 = [repmat(a1,1,M),0];
pss_r2 = [repmat(a2,1,M),0];
pss_r3 = [repmat(a3,1,M),0];
pss_r4 = [repmat(a4,1,M),0];
pss_r5 = [repmat(a5,1,M),0];
pss_r6 = [repmat(a6,1,M),0];
% 阵元采用不同编码调制方式
jamR2 = jamR.*pss_r1;
jamR3 = jamR.*pss_r2;
jamR4 = jamR.*pss_r3;
jamR5 = jamR.*pss_r4;
jamR6 = jamR.*pss_r5;
jamR7 = jamR.*pss_r6;
jamRR = [jamR2.',jamR3.',jamR4.',jamR5.',jamR6.',jamR7.'].';
jamRR1 = 1/N*a_theta1'*(a_theta1*ones(1,nr).*jamRR)*SNR1;
jamRR2 = 1/N*a_theta2'*(a_theta1*ones(1,nr).*jamRR)*SNR1;
jamRR3 = 1/N*a_theta3'*(a_theta1*ones(1,nr).*jamRR)*SNR1;
jamRR1 = fftshift(fft(jamRR1)); %距离向FFT
jamRR1=jamRR1.*Hr.';
jamRR1=ifft(ifftshift(jamRR1));
G=abs(jamRR1);
gm=max(G);
G=G.*(G>0);
[pks5,~] = findpeaks(G,'NPeaks',7,'minpeakheight',0.0001*gm,'MinPeakDistance',245);
jamRR2 = fftshift(fft(jamRR2)); %距离向FFT
jamRR2=jamRR2.*Hr.';
jamRR2=ifft(ifftshift(jamRR2));
G=abs(jamRR2);
gm=max(G);
G=G.*(G>0);
[pks6,~] = findpeaks(G,'NPeaks',7,'minpeakheight',0.0001*gm,'MinPeakDistance',245);
jamRR3 = fftshift(fft(jamRR3)); %距离向FFT
jamRR3=jamRR3.*Hr.';
jamRR3=ifft(ifftshift(jamRR3));
G=abs(jamRR3);
gm=max(G);
G=G.*(G>0);
[pks7,~] = findpeaks(G,'NPeaks',7,'minpeakheight',0.0001*gm,'MinPeakDistance',245);
amp_ratio12m = pks5./pks6;
amp_ratio13m = pks5./pks7;
lenm = length(amp_ratio12m);
omigam = zeros(lenm,2);
for j = 1 : lenm
omigam(j,:) = [amp_ratio12m(j), amp_ratio13m(j)];
end
summ = 0;
temp_truem = truem;
for k = 1 : lenm
A = ones(lenm,1)*omigam(k,:) - temp_truem;
dis_temp = sqrt(sum(A.^2, 2));
[dis_temp, index] = sort(dis_temp);
temp = dis_temp(1);
summ = summ + temp;
temp_truem(index(1),:) = temp_truem(index(1),:) - ones(1,2)*100;
end
fitness(1,i) = summ;
end
% index记录排序后每个值原来的行数
[fitness, index] = sort(fitness); % 将适应度函数值从小到大排序
% index(1:parent_number)
% 前parent_number个cost较小的个体在种群population中的行数
% 选出这部分(parent_number个)个体作为父母,其实parent_number对应交叉概率
population = population(index(1:parent_number), :); % 先保留一部分较优的个体
% 可以看出population矩阵是不断变化的
% cost在经过前面的sort排序后,矩阵已经改变为升序的
% cost(1)即为本代的最佳适应度
best_fitness(generation) = fitness(1); % 记录本代的最佳适应度
% population矩阵第一行为本代的精英个体
elite(generation, :) = population(1, :); % 记录本代的最优解(精英)
% 若本代的最优解已足够好,则停止演化
if best_fitness(generation) < minimal_cost
last_generation = generation;
break;
end
% 交叉变异产生新的种群
% 染色体交叉开始
for child = 1:2:child_number % 步长为2是因为每一次交叉会产生2个孩子
% cumulative_probabilities长度为parent_number
% 从中随机选择2个父母出来 (child+parent_number)%parent_number
mother = find(cumulative_probabilities > rand, 1); % 选择一个较优秀的母亲
father = find(cumulative_probabilities > rand, 1); % 选择一个较优秀的父亲
% ceil(天花板)向上取整
% rand 生成一个随机数
% 即随机选择了一列,这一列的值交换
crossover_point = ceil(rand*number_of_variables); % 随机地确定一个染色体交叉点
% 假如crossover_point=3, number_of_variables=5
% mask1 = 1 1 1 0 0
% mask2 = 0 0 0 1 1
mask1 = [ones(1, crossover_point), zeros(1, number_of_variables - crossover_point)];
mask2 = not(mask1);
% 获取分开的4段染色体
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。

🌈4 Matlab代码、数据、文章
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取
























 3376
3376

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








